【图神经网络】社区检测
社区检测
社区是许多网络的特性,一个特定的网络可能有多个社区,社区内的节点之间连接紧密。
网络节点在社区内部形成紧密的连接,而在社区之间则形成松散连接。
社区检测技术对于社交媒体算法来说非常有用,可以发现具有共同兴趣的人并将他们紧密连接在一起。社区检测也可以应用于机器学习中,用于检测具有相似属性的群组,并出于各种原因提取这些群组。例如,这种技术可以用于发现社交网络或股票市场中的操纵性群体。
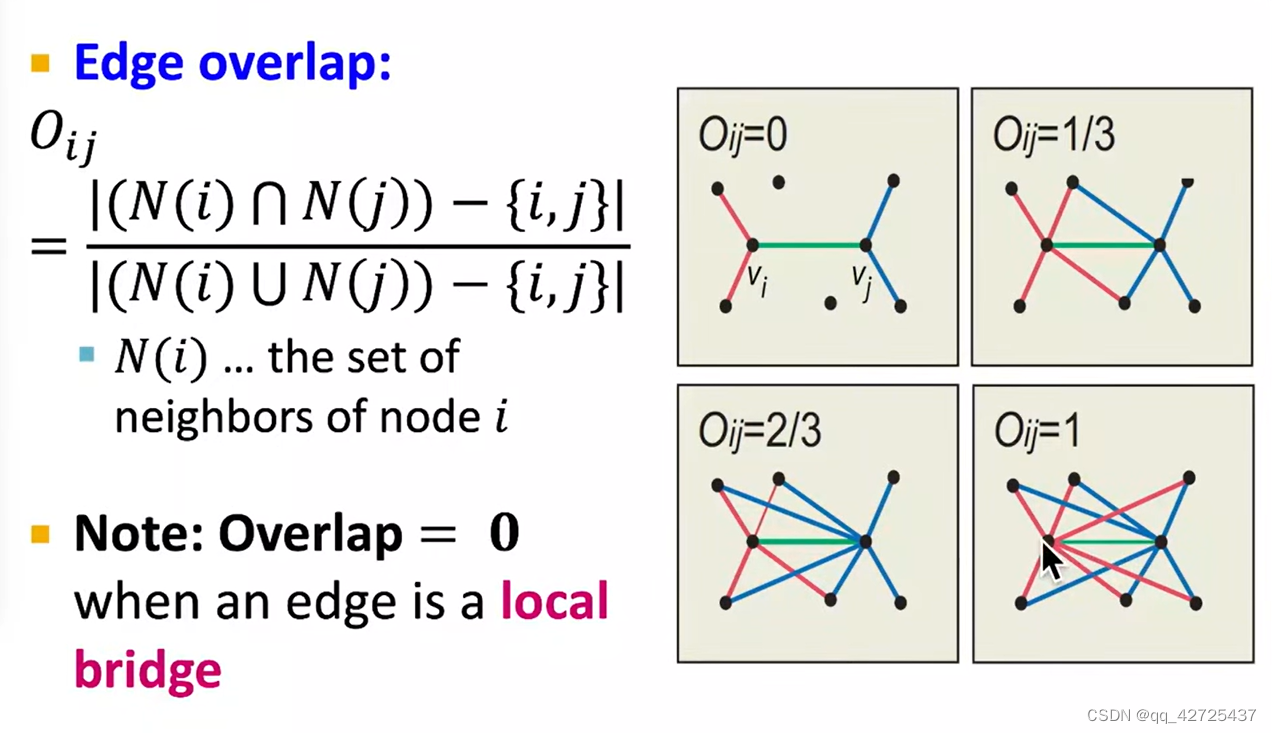
Edge Overlap
评估当前边的重叠性质,如果重叠度高,就应该是社区内部的边,反之,是社区之间的边。
modularity
判断社区划分的好坏
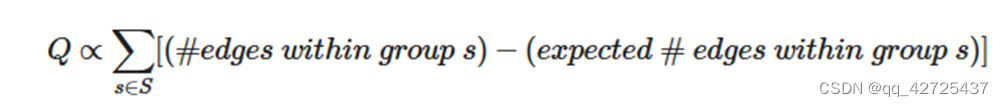
每个社区中边的数量与期望边(随机分配的)的数量之间的差值。这个值越大,社区划分越好。
需要构建一个null模型来得到期望边数量
下面是i和j之间期望数量为
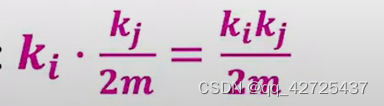
k
i
k_i
ki?是节点i的度,总共有n个节点、m个边,边是双向的,所以从i节点射出的边有
k
j
2
m
\frac{k_j}{2m}
2mkj??的概率指向节点j。
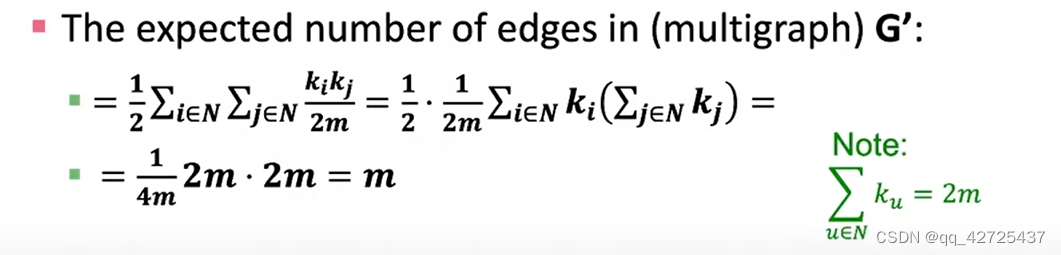
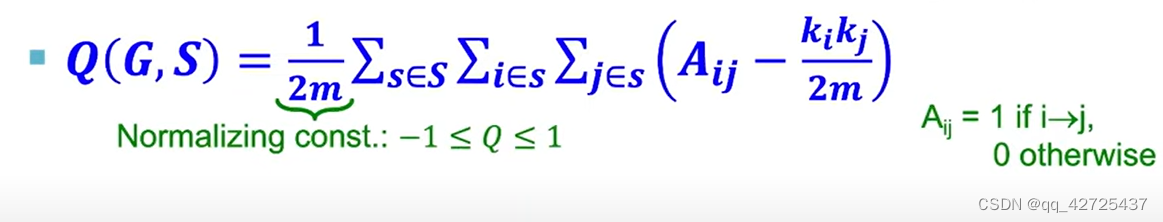
下面的式子由上面的式子推导出来
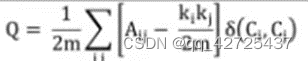
如果i和j属于一个社区,
δ
=
1
\delta=1
δ=1否组为0.
Louvain Community Detection
作为一种用于大型网络的快速社区检测算法。该方法基于模块度(modularity),试图最大化社区内实际边的数量与预期边的数量之间的差异。然而,在网络中优化模块度是NP难问题,因此需要使用启发式算法。Louvain算法分为两个阶段的迭代重复执行:
1.节点的局部移动
2.网络的聚合
该算法从一个具有N个节点的加权网络开始。在第一阶段中,算法为网络中的每个节点分配一个不同的社区。然后对于每个节点,考虑其邻居,并通过将该节点从当前社区移除并放置在邻居社区中来评估模块度的增益。如果增益为正且最大化,则将节点放置在邻居社区中。如果没有正的增益,则节点将保留在同一社区中。这个过程重复应用于所有节点,直到没有进一步的改进为止。Louvain算法的第一阶段在获得模块度的局部极大值时停止。在第二阶段中,算法构建一个新的网络,将第一阶段发现的社区作为超级节点。完成第二阶段后,算法将重新应用第一阶段到得到的网络上。这些步骤重复进行,直到网络不再发生变化且达到最大的模块度。
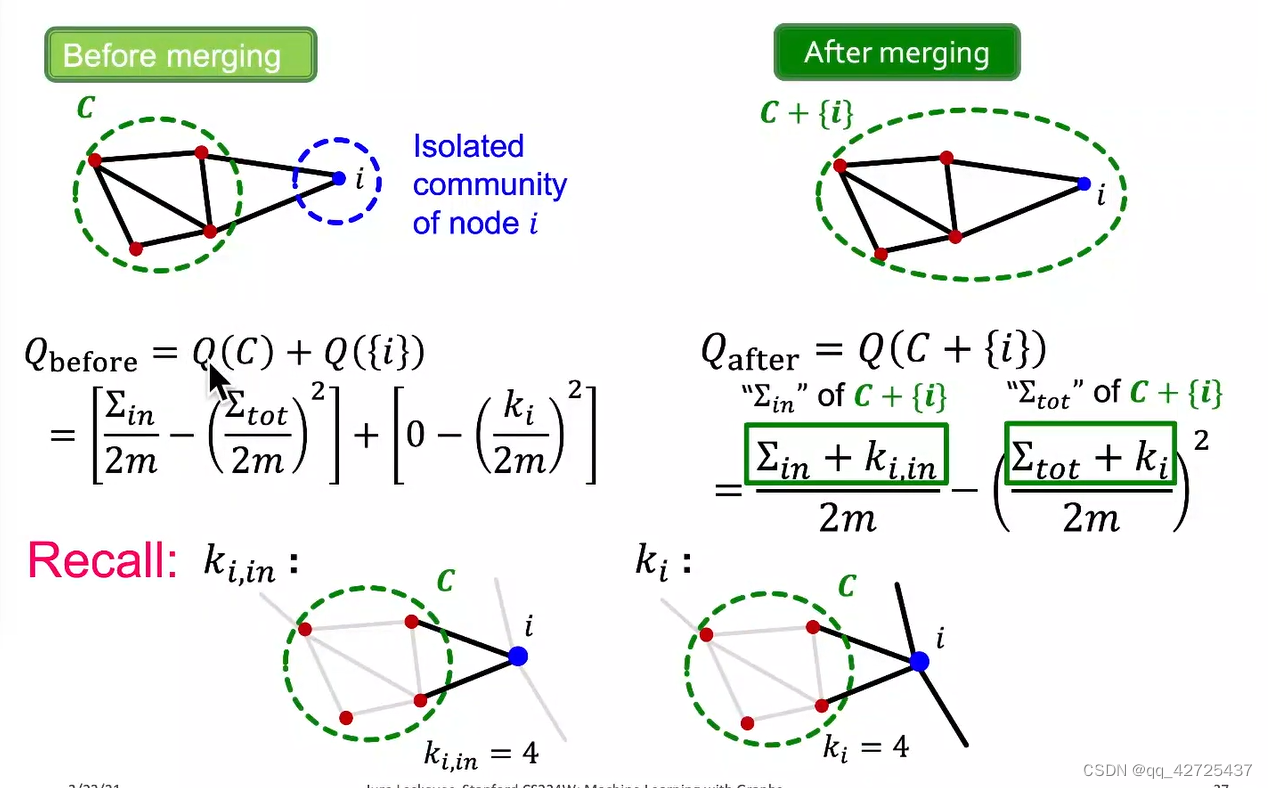
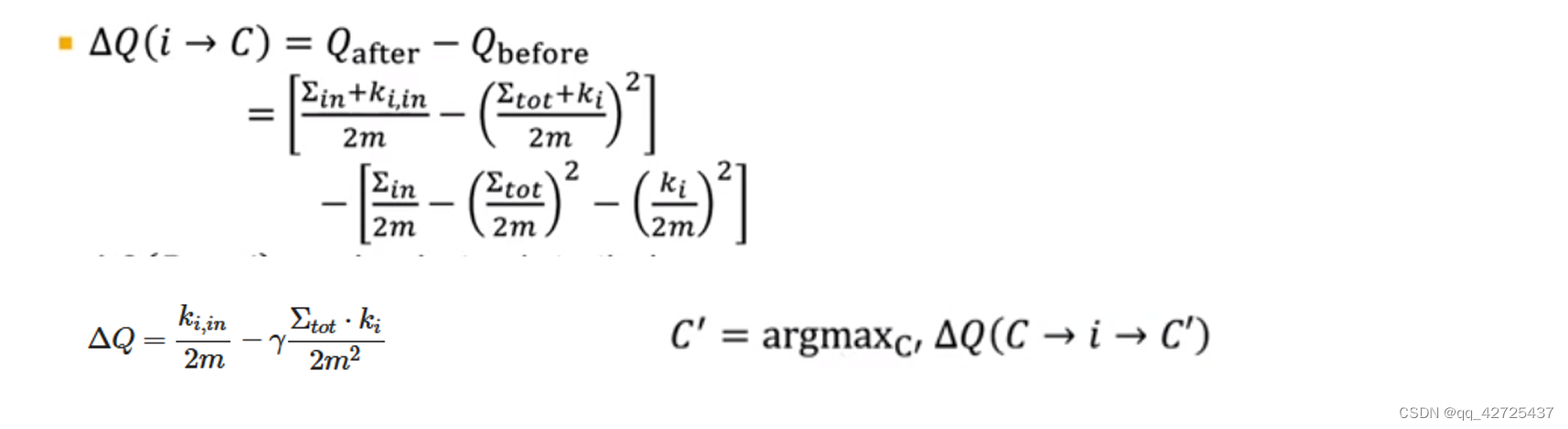
通过推导,可以得到将节点i加入c社区的q变化,同理,可以得到将节点i从社区中删除的q变化,得到最终的
Δ
Q
\Delta Q
ΔQ
BigCLAM
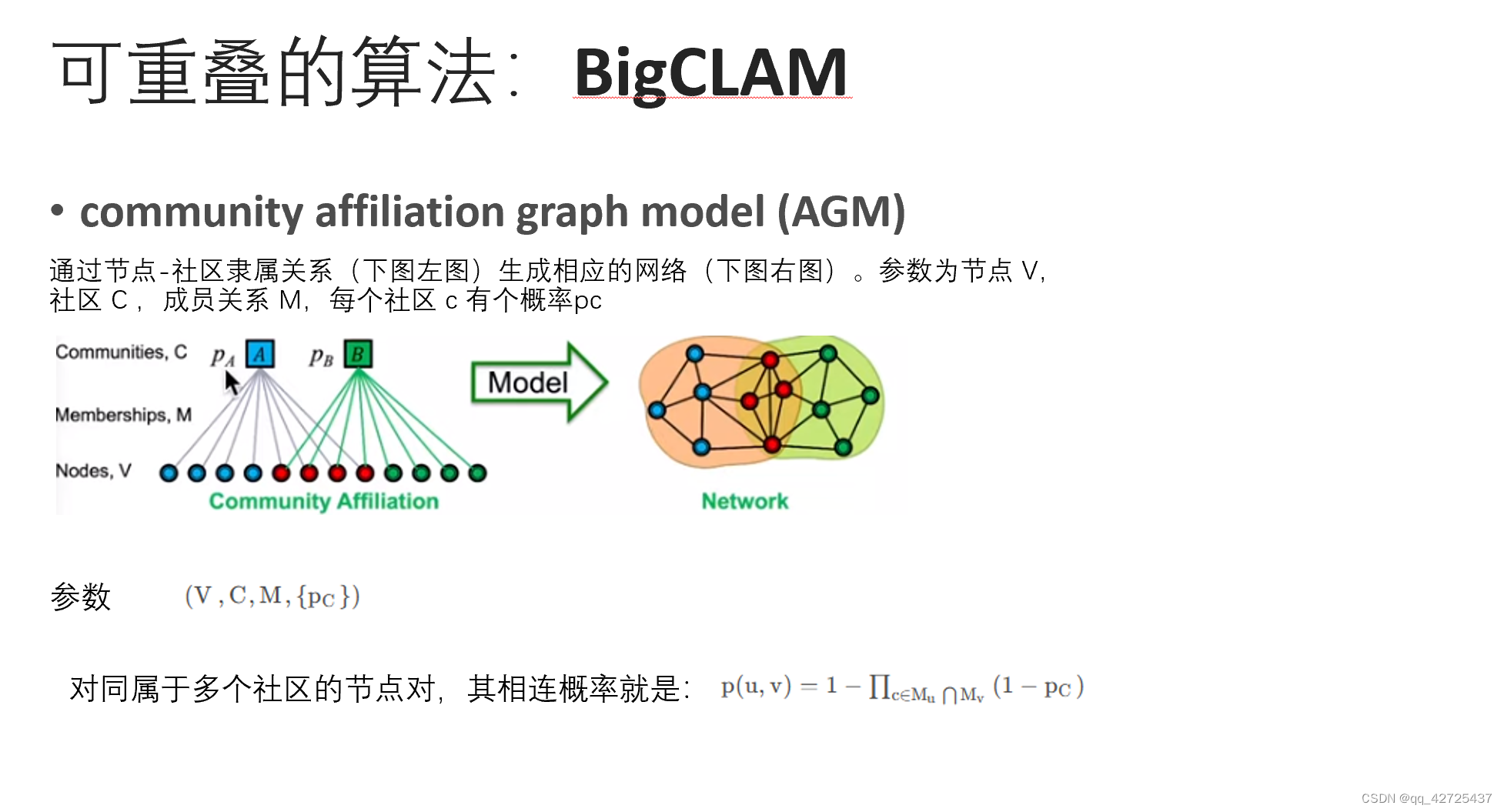
对于每个社区中两个节点是否相连的概率为pc
通过能够得到模型F使得从模型F生成图G的概率最大

这样就得到了u,v节点连接的概率
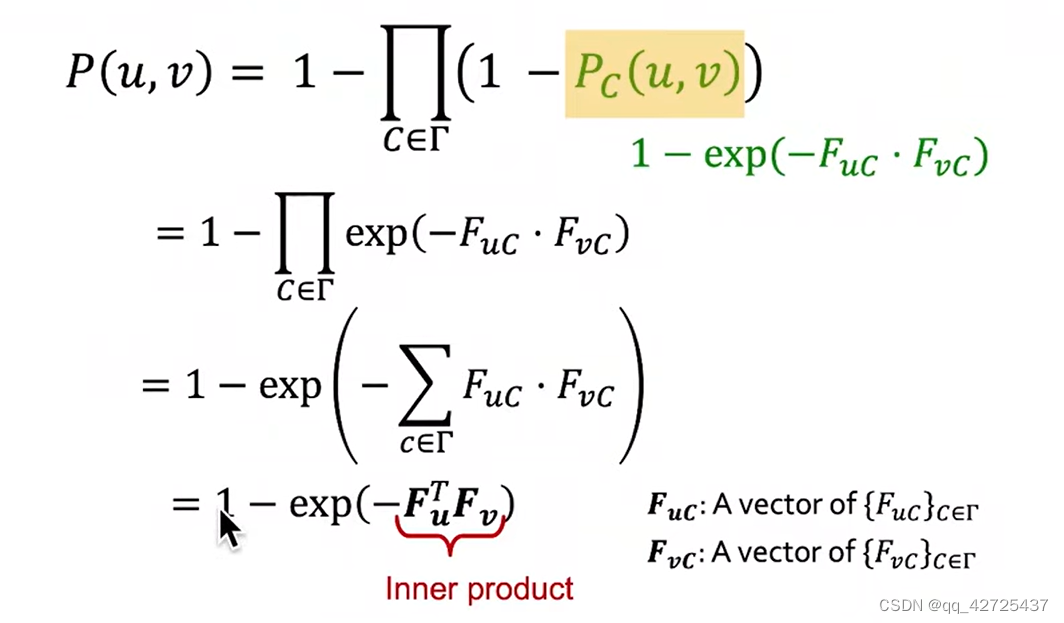


本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!