回归分析笔记

回归分析

回归分析: 寻找两个或多个变量之间的函数关系(相关关系)

一元和线性

$$\begin{array}{rl}y& ={\beta }_0+{\beta }_{1}x+\epsilon \end{array}$$

• 误差项$\epsilon$是一个期望值为0的随机变量，即$E(\epsilon )=0$, 对于一个给定的$x$值, $y$的期望值为$E(y)={\beta }_0+{\beta }_{1}x$
• 对于所有的$x$值, $\epsilon$的方差${\sigma }^2$都相同
• 误差项$\epsilon$是一个服从正态分布的随机变量，且相互独立

$$\begin{array}{rl}{\beta }_1& =\frac{\sum x_i{y}_i?n\overline{x}\overline{y}}{\sum x^2?n\overline{x}}\\ {\beta }_0& =\overline{y}?{\beta }_1\overline{x}\end{array}$$

回归显著性校验:

• 总离差平方和(SST): $\sum (y_i?\overline{y}{)}^2$
• 残差平方和(SSE): $\sum (y_i?{\hat{y}}_i{)}^2$
• 回归平方和(SSR): $\sum ({\hat{y}}_i?\overline{y}{)}^2$

$$\begin{array}{rl}SST& =\sum (y_i?\overline{y}{)}^2\\ & =\sum [({\hat{y}}_i?\overline{y})+(y_i?{\hat{y}}_i){]}^2\\ & =\sum ({\hat{y}}_i?\overline{y}{)}^2+\sum (y_i?{\hat{y}}_i{)}^2+2\sum ({\hat{y}}_i?\overline{y})(y_i?{\hat{y}}_i)\\ & =\sum ({\hat{y}}_i?\overline{y}{)}^2+\sum (y_i?{\hat{y}}_i{)}^2+0\\ & =SSR+SSE\end{array}$$

相关系数$r$

$$r^2=\frac{SSR}{SST}=\frac{\sum ({\hat{y}}_i?\overline{y}{)}^2}{\sum (y_i?\overline{y}{)}^2}=1?\frac{\sum (y_i?\hat{y}{)}^2}{\sum (y_i?\overline{y}{)}^2}$$

• $r$越接近于1，相关性越强
• $r\in [0,1]$

$F$检验

• 提出假设: 线性关系不显著
• 计算检验统计量$F$

$$\begin{array}{rl}F& =\frac{SSR/1}{SSE/(n?2)}=\frac{\sum ({\hat{y}}_i?\overline{y}{)}^2}{\sum ({\hat{y}}_i?y_i{)}^2/(n?2)}～F(1,n?2)\end{array}$$

• 确定显著性水平$\alpha$，并根据分子自由度1和分母自由度(n-2)找出临界值$F_{\alpha }$作出决策: 若$F\ge F_{\alpha }$, 拒绝假设; 否则接受假设。(概率论与数理统计)
• $F$越大线性关系越显著

$F$与$r$的关系

$$F=\frac{(n?2)r^2}{1?r^2}$$

• 说明$F$检验和$r$相关系数的一致性

例题

重复测量的分析

对于同一个$x$重复测量得到$y$的值

• 离差平方和: $S$

• 残差平方和: $Q$

• 回归平方和: $U$

• 误差平方和: $Q_E$

• 失拟平方和: $Q_L$

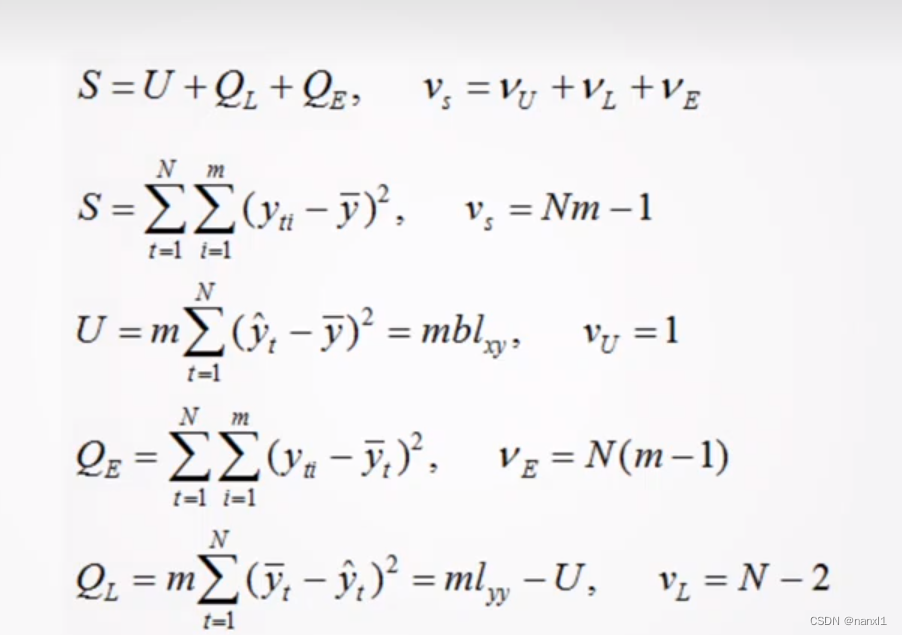
两个变量都有误差的一元线性回归

• $\lambda$衡量了误差偏向的方向
• 问题: 如何通过先验信息测出$\lambda =\frac{{\sigma }_x^2}{{\sigma }_y^2}$?

一元非线性

• 化非线性为线性问题的求解

典型的化解方法

$$\begin{array}{rl}y& =\alpha e^{\beta x}\\ y& =\alpha x^{\beta }\\ y& =\frac{x}{\alpha x+\beta }\\ y& =\alpha +\beta \log x\\ y& =\frac{1}{\alpha +\beta e^{?x}}\end{array}$$

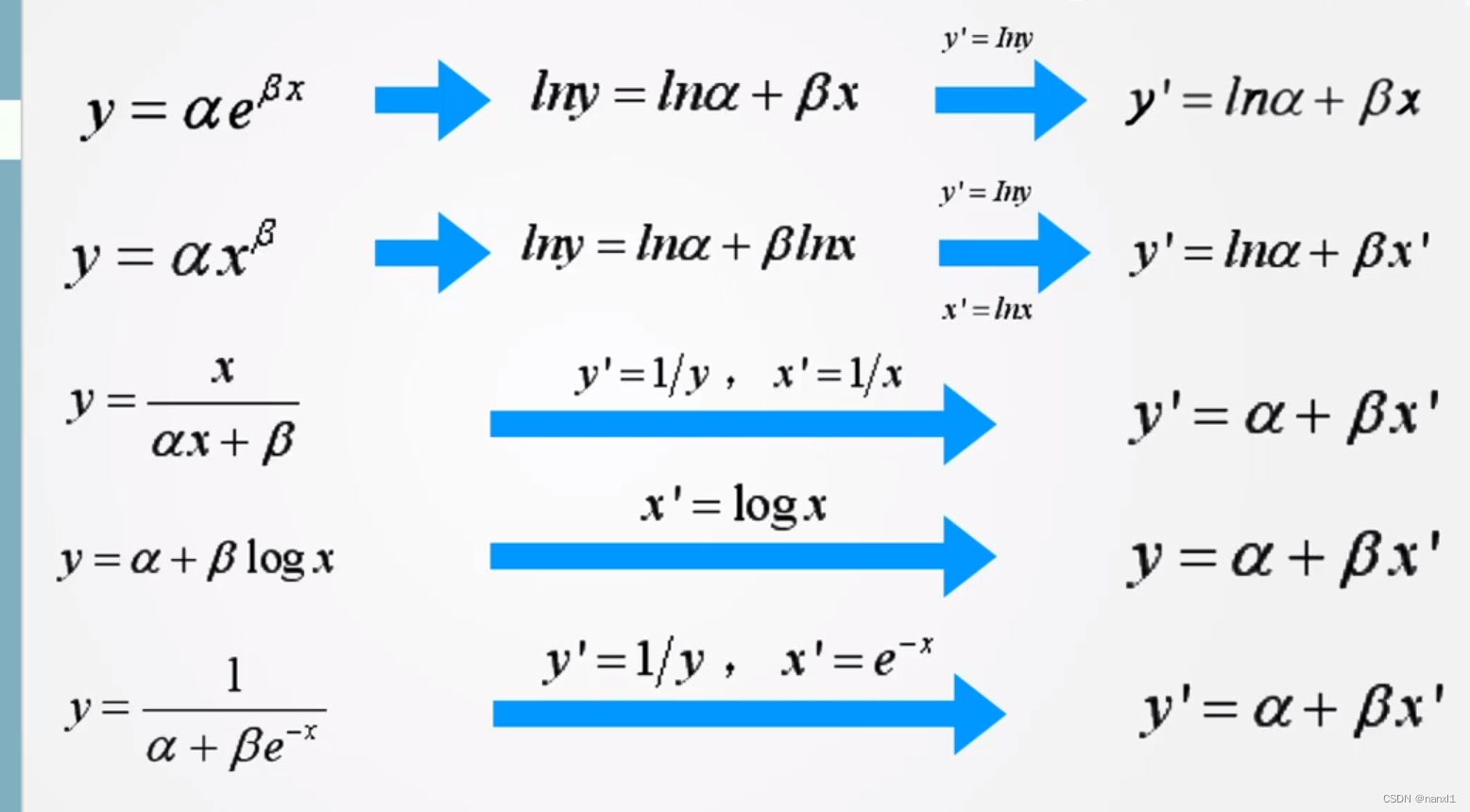
具体步骤

• 根据散点图确认非线性回归方程模式
• 把非线性回归方程转换为线性回归方程
• 依据线性回归方程进行求解
• 再转换为非线性回归方程

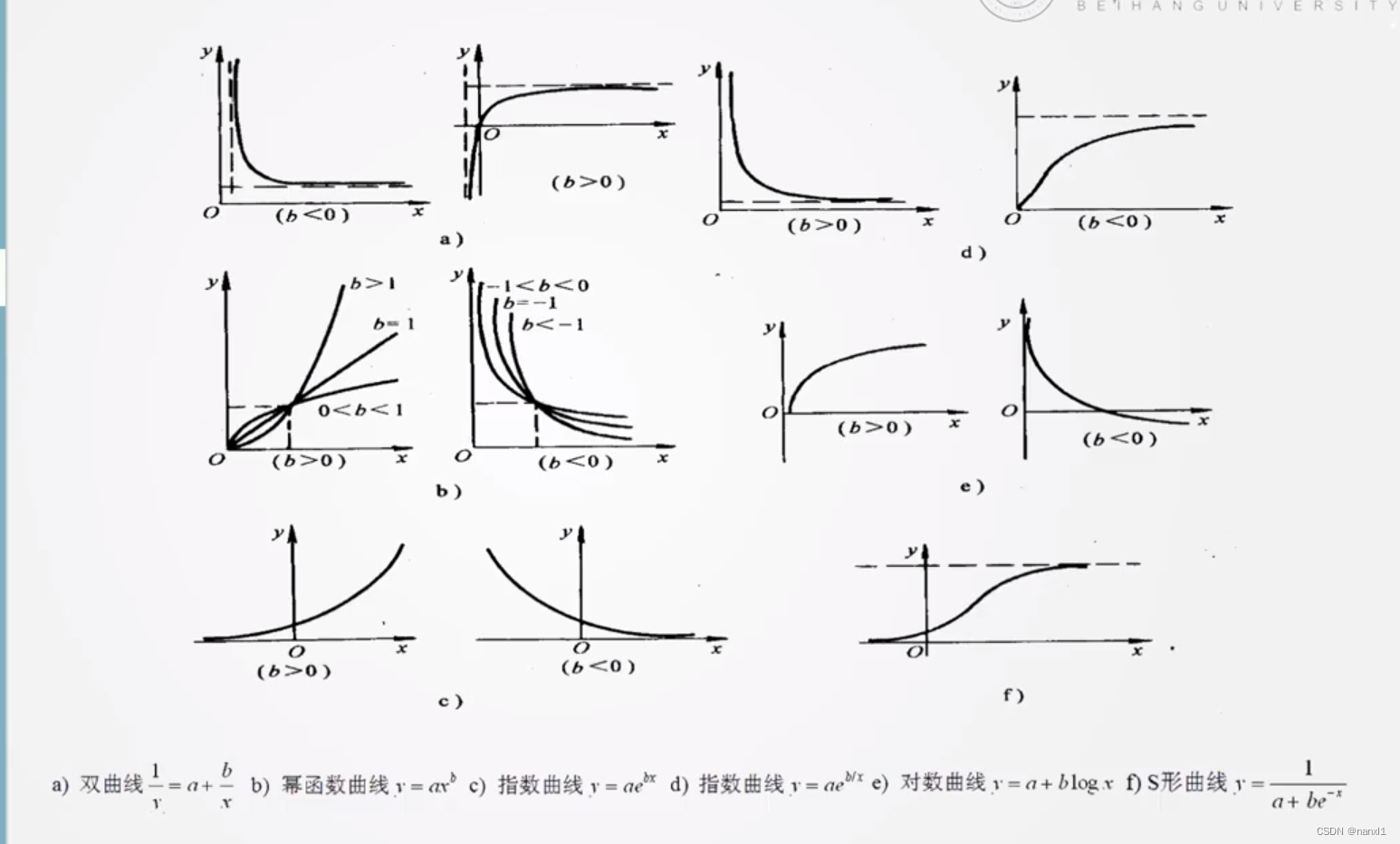
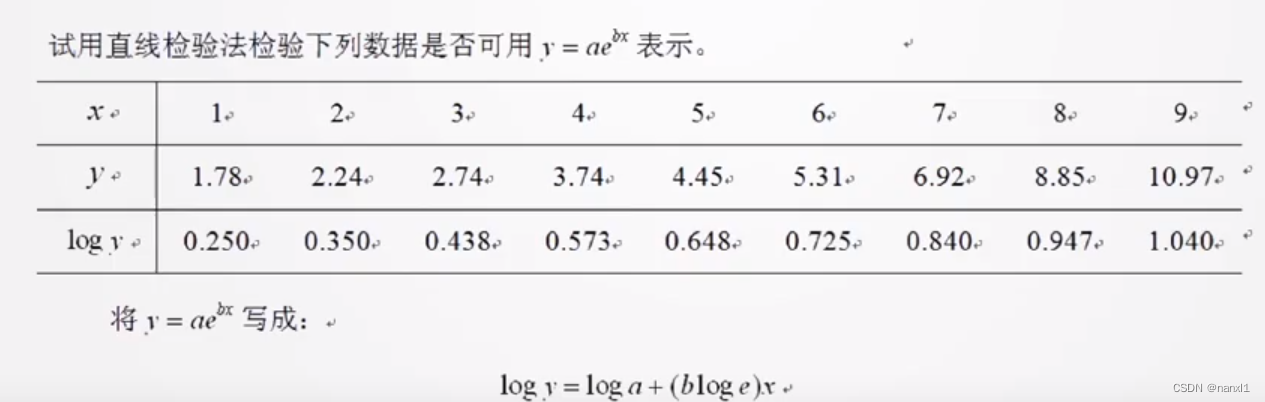
• 观察数据是否符合某个曲线, 若符合则可以套用公式试试效果
• 以下是常见的曲线

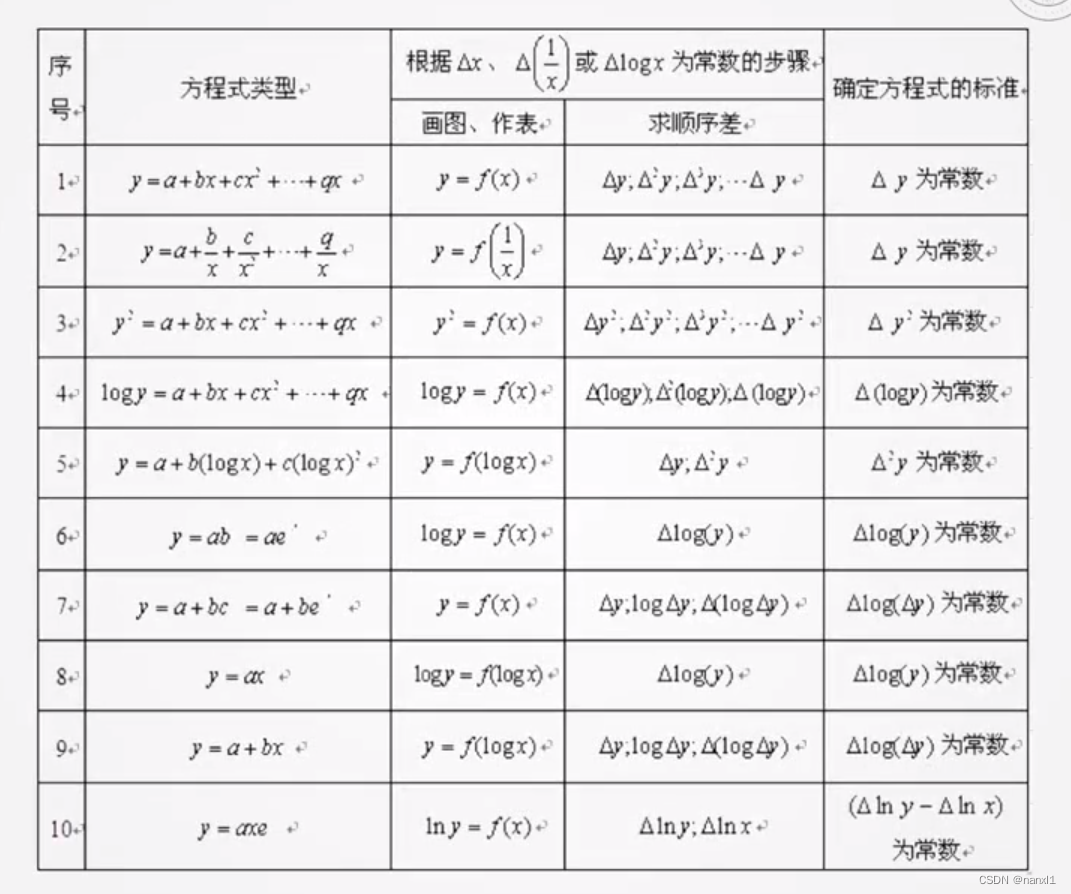
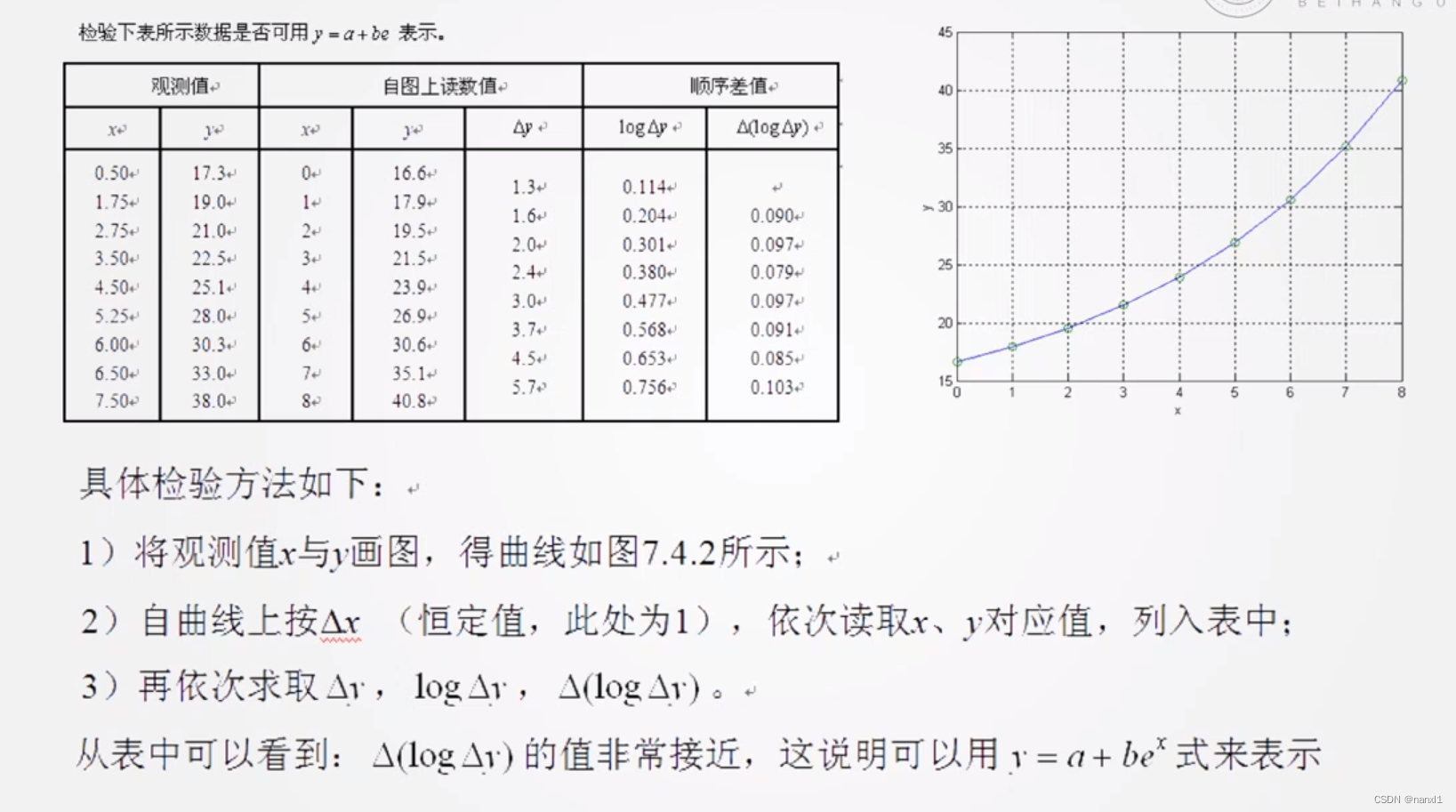
• 在实际情况下，可能有多条曲线符合。这时需要将所有曲线都尝试一遍，然后做显著性校验，选取显著性校验最好的曲线作为结果。

多元线性

$$\begin{array}{rl}\hat{y}& =b_0+b_1{x}_1+b_2{x}_2+...+b_M{x}_M\\ 由& 最小二乘法:\\ Q& =\sum _{t=1}^M(y_t?{\hat{y}}_t)=\sum _{t=1}^M(y_t?b_0?b_1{x}_{t1}?b_2{x}_{t2}?...?b_M{x}_{tM}{)}^2=最小\\ & ?\begin{array}{l}\frac{?Q}{?b_0}=?2{\sum }_{t=1}^M(y_t?b_0?b_1{x}_{t1}?b_2{x}_{t2}?...?b_M{x}_{tM})=0\\ \frac{?Q}{?b_i}=?2{\sum }_{t=1}^M(y_t?b_0?b_1{x}_{t1}?b_2{x}_{t2}?...?b_M{x}_{tM})=0\\ i=1,\mathrm{2......}M\end{array}\end{array}$$

矩阵形式:
$$\begin{array}{rl}(X^{T}X)b& =X^{T}Y\\ b=A^{?1}& B=(X^{T}X{)}^{?1}{X}^{T}Y\end{array}$$
另一种方法
$$\begin{array}{rl}\hat{y}& ={\mu }_0+b_1(x_1?{\overline{x}}_1)+b_2(x_2?{\overline{x}}_2)+...+b_M(x_M?{\overline{x}}_M)\\ & Ab=B\\ 其& 中:\mu =b_1{\overline{x}}_1+b_2{\overline{x}}_2+...+b_M{\overline{x}}_M=\overline{y}\end{array}$$

• 要求的系数$b$比上一种方法少一个，矩阵维数由$M+1\to M$

• 计算量减少

$F$检验

实例

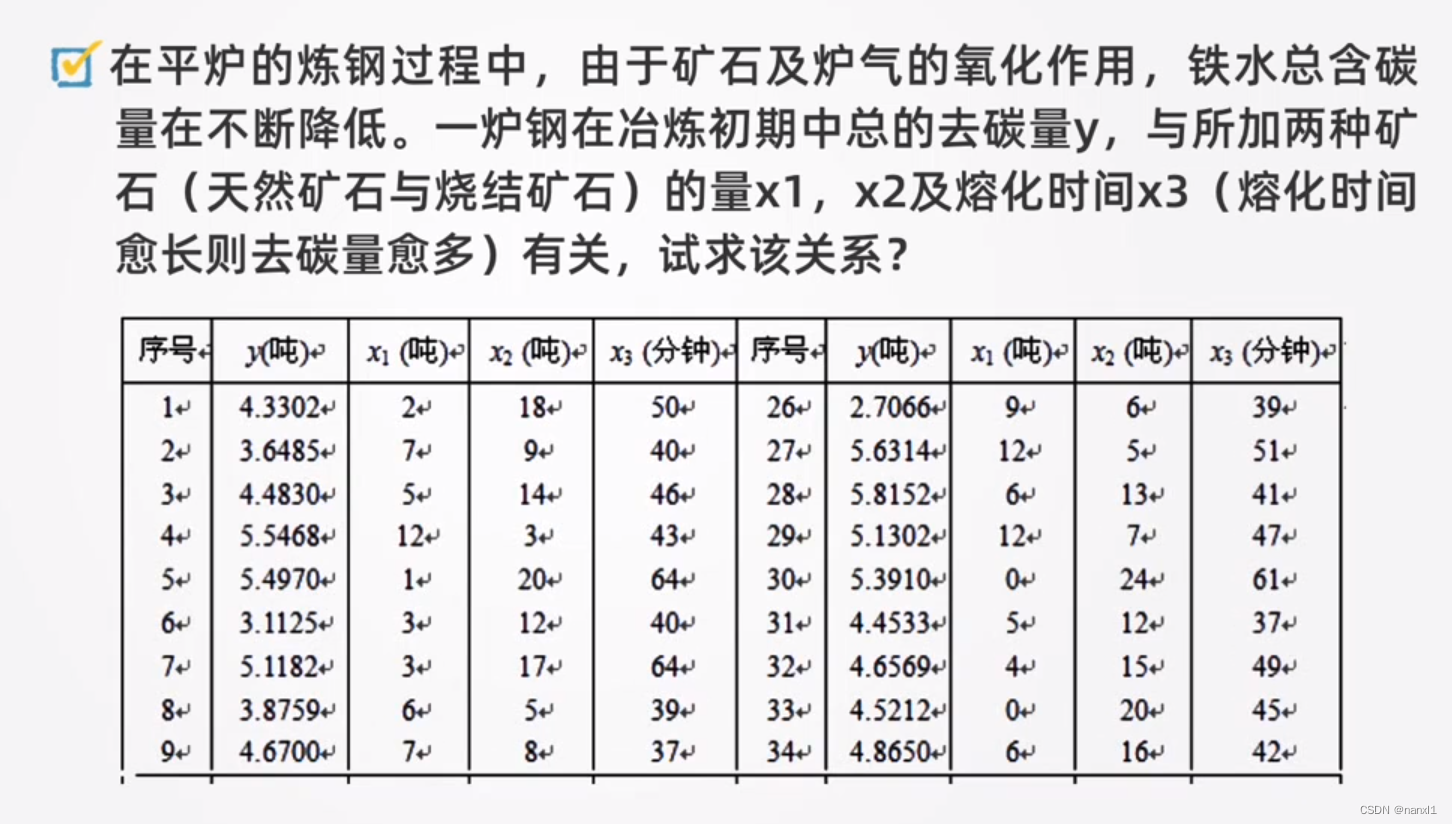
参考资料

【名校公开课-误差理论与数据处理-钱政 | 北京航空航天大学】