非递归方式遍历二叉树的原理

一、递归遍历代码

// 先序遍历
void PreOrder(BiTNode *T){
	if (T!=NULL){
		visit(T);  // 最简单的visit就是printf(T->data)
		PreOrder(T->lChild);
		PreOrder(T->rChild);
	}
}

// 中序遍历
void InOrder(BiTNode *T){
	if (T!=NULL){
		InOrder(T->lchild);
		visit(T);
		InOrder(T->rchild);
	}
}

// 后序遍历
void PostOrder(BiTNode *T){
	if (T!=NULL){
		PostOrder(T->lchild);
		PostOrder(T->rchild);
		visit(T);
	}
}

二、三种遍历过程示意图以及非递归遍历相关原理

以表达式a*b-c为例构建二叉树，则对该二叉树进行前序遍历就是前缀表达式，中序遍历就是中缀表达式，后序遍历就是后缀表达式。三种遍历过程示意图如下：

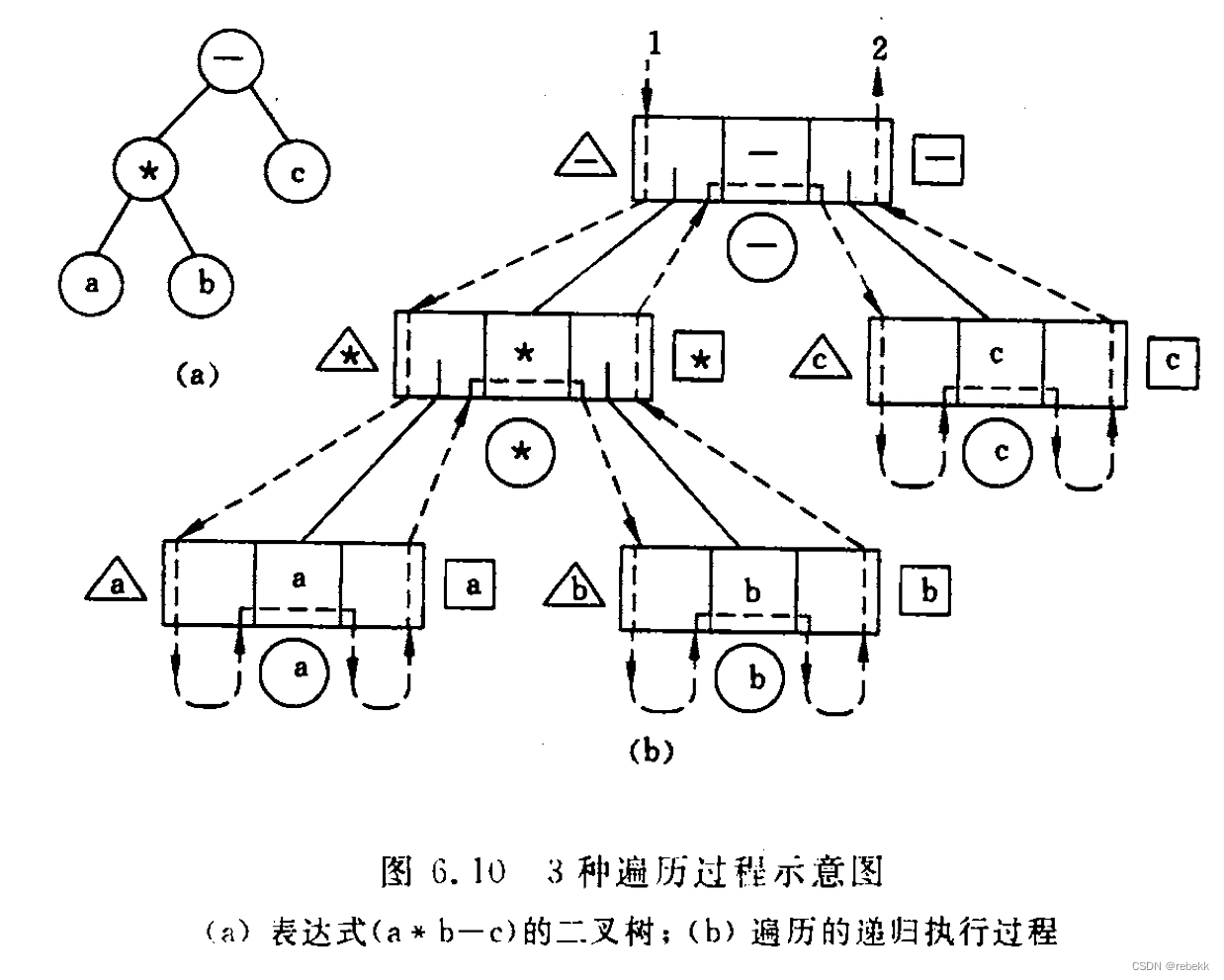
虚线表示递归执行过程（箭头向下表示前往更深一层的递归调用，箭头向上表示从递归调用推出返回）；虚线旁的三角形、圆形、方形内的字符分别表示在先序、中序、后序遍历二叉树过程中访问节点时输出的信息。

从上图可知（也可从去掉visit的代码得知），从递归执行过程的角度来看先序、中序、后序遍历，是完全相同的。仿照递归算法执行过程中递归工作栈的状态变化状况可直接写出相应的非递归算法。

对于中序遍历递归算法，当栈顶记录中的指针非空时，应遍历左子树，即指向左子树根的指针进栈；若栈顶记录中的指针为空，则应退至上一层。若是从左子树返回，则应访问当前层即栈顶记录中指针所指的根节点；若是从右子树返回，则表明当前层的遍历结束，应继续退栈。

从另一角度看，这意味着遍历右子树时不再需要保存当前层的根指针。

以此可以更加深刻理解那句“只有后序遍历可以找到一个节点的祖先”。
因为前序、中序遍历，遍历到右子树节点时，右子树的左兄弟和父节点都遍历完成，且不会在后面的遍历过程中被需要，因此可直接退栈。所以这两种遍历方式并不能找不到一个右子树节点的所有祖先。

而对于后序遍历，根据左右根的顺序，若当前节点是一个左子树的节点，那么：1）其右兄弟还未进栈；2）其父节点进栈了但没有被访问而弹出。因此栈中保存的就是该节点到其祖先节点的路径；
若当前节点是一个右子树的节点，那么：1）其左子树在返回根节点之前就被访问并弹出了；2）其父节点进栈了但没有被访问而弹出。

因此可知后序遍历可以找到一个节点的祖先（栈中有且只有所有祖先所串成的整个路径）