数位dp详解，记忆化搜索，递推，OJ精讲

前言

数位DP亦即称数位动态规划，是动态规划的又一子问题，难度尚可，题目思想相近，甚至可以提炼出模板，当然，如果对动态规划有着一定的基础，如最长递增子序列（LIS），最长公共子序列（LCS），记忆化搜索，状态机，背包问题等有着一定的了解，在未了解数位dp的情况下一般也能通过分析设计状态，进行求解，但是我们对于动态规划种种问题的分类归纳，有助于我们呢更好地掌握动态规划的思想，提升思维的高度。

---

引例-不降数

科协里最近很流行数字游戏。某人命名了一种不降数，这种数字必须满足从左到右各位数字成小于等于的关系，如 123，446。现在大家决定玩一个游戏，指定一个整数闭区间 [a,b]，问这个区间内有多少个不降数。

对于全部数据，1 <= a <= b <= 2 ^ 31 - 1。

如果我们暴力预处理出所有的不降数，那么每个数字需要O?（C为数字位数）时间判断，最终可以达到O(1e9 * C)的时间复杂度，显然无法接受，我们自然要另辟蹊径。

前置知识

差分转换

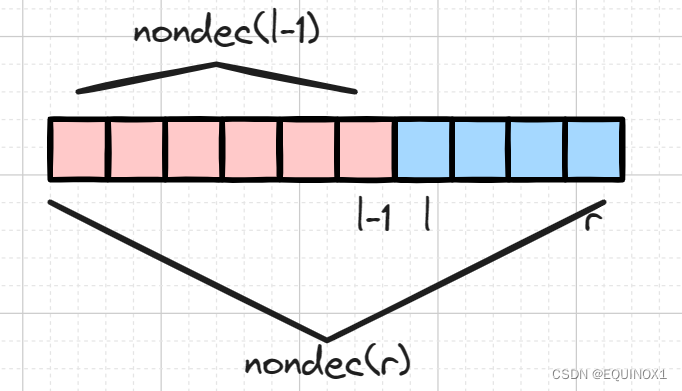
对于区间解我们的常用做法就是差分法分解。

对于[0 , r]区间内的不降数的数目nondec?，[0 , l - 1]内的不降数的数目nondec(l - 1)，显然满足

nondec? - nondec(l - 1) = [l , r]内的不降数数目

枚举技巧

对于一个十进制数字x，假设从高位到低各位分别为dn,dn-1,dn-2……我们去枚举小于等于x的数字an,an-1,an-2……，如果按照数位从高到低枚举，对于第n位自然要满足an <= dn，但是我们接着枚举会发现：

• 如果an < dn，那么an-1 ∈ [0 , 9]
• 如果an = dn，那么an-1 ∈ [0 , dn-1]

例如给定数字2024，我们当前枚举1abc，即第一位枚举的1，那么后面可以任意取，如19bc，18bc或者199c或者1999等等，都是小于2024的

那么可以推广：对于K进制数字x，高位到低各位分别为dn,dn-1,dn-2……，枚举小于等于x的数字i，高位到低各位分别为an,an-1,an-2……，假如已经枚举前缀pre，当前该枚举第j位，用lim来代表pre是否小于dn-1…dj-1，真为小于，则:

• lim为true，那么aj ∈ [0 , K-1]
• lim为false，那么an-1 ∈ [0 , dj]

前缀状态

所谓前缀就是指前面提到的已经枚举前缀pre，但是前缀状态要和题目具体条件结合，如我们引例要求我们求不降数，那么我们只需要记录当前枚举位的上一位作为pre即可，因为只需要上一位就能判断我们当前取什么范围的数字才能保证不降性

同样的，如果我们要求求出区间内不含连续1的数字数目，那么pre只需要0/1两种状态就能表示。

状态分析

数位之间存在着某种可传递关系，我们尝试用动态规划来降低暴力解法的时间复杂度，那么自然要进行动态规划的分析步骤。

状态设计

设计状态是为了把大问题拆解为小问题。

仍然是引例-不降数问题，我们按位枚举过程中，如果前缀状态为pre，还需剩下n位没有枚举，我们知道pre会对剩下n位的枚举范围产生限制，也就是说，对于前缀状态为pre的不降数是pre限制下长度为n位的不降数的数目，而我们前面说了可以将pre是否等于前缀表示为lim。

那么我们不妨设计状态f(n,pre,lim)，表示剩余n位还需枚举，前缀状态为pre，已经枚举前缀是否小于给定数字x对应前缀是否用lim表示（lim为真表示已经枚举前缀小于x对应前缀）时的不降数数目。对三个维度具体分析：

• n代表剩下n位没有枚举，n代表高位，如201234，1就是第4位
• pre就是前缀状态，如我们当前枚举1123xxx，x代表未枚举的位，那么前缀状态就是已经枚举前缀的最后一位即3
• lim代表已枚举前缀是否小于x对应前缀，也可以理解为an……aj-1中是否存在ak < dk，由于保证 ak <= dk，如果存在任意ak < dk，那么可以保证ak以后的所有位任意取都可以小于给定数字。如给定十进制数字45521，当前枚举前缀3xxxx，那么即使后面全取9即39999，仍有39999 < 45521

状态转移

我们将给定的十进制数字x做如下表示：
$$x=d_n{d}_{n?1}...d_1，其中dn代表最高位，d1代表最低位$$
则有如下状态转移方程：
$$f(n,pre,lim)=\sum _{k=pre}^{ceil}f(n?1,k,limork<ceil)$$

• k表示第n位取的数字，由于保证不降性，所以从pre开始取，不超过最大值ceil，其中ceil
  • 如果lim = true，则ceil = 9
  • 否则，ceil = d[n]
• 转移方程中求和公式中的第三维(lim or k < ceil)也可改成(lim or k < d[n])，效果一样，读者可以自己思考一下

初始状态

对于上述的状态转移方程，我们可以通过递归求解，那么此时的初始状态就是我们n = 0时的递归出口，即还剩0位需要枚举，那么此时的不降数就是我们已经枚举的前缀，直接返回1即可。

记忆化搜索

我们发现如果求解一个问题，会有很多重叠子问题，这就导致了大量重复计算，所以我们可以通过记忆化进行剪枝，即用三维数组f[n][pre][lim]来保存已经求出的状态。

我们观察下面这张递归树。

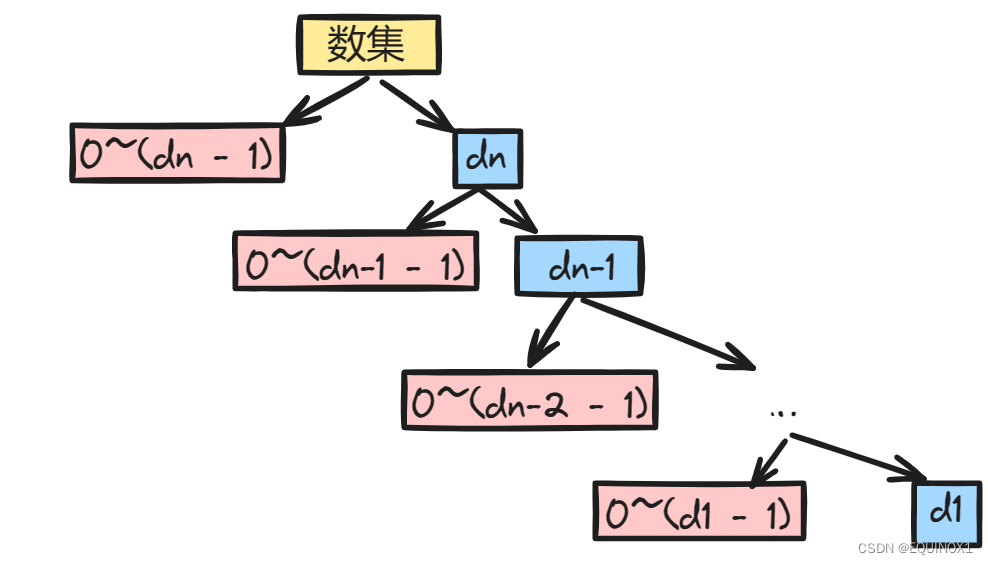
对于我们的记忆化数组的第三个维度[lim]只有两个取值0/1，而且根据我们对于lim的定义，当lim为false时，表示之前枚举的前缀和给定数字的前缀x一致，对应递归树上的路径只有唯一一条（图中最右侧的蓝色路径），所以即然第三个维度只有两种取值，且有一种取值对应的递归路径是唯一的，那么我们不妨将第三维优化掉，只记忆化第三维为true的情况，对于即我们图中红色节点被剪枝

而如果要求蓝色路径，那么直接求即可。这样我们优化三维为一维。

至此，我们只需要用二维数组f[n][pre]代表剩余n位，前缀状态为pre时的不降数个数。

对于我们的递归函数，如果递归函数参数为f(n , pre , false)，那么采用普通深搜，如果是f(n , pre , true)，那么采用记忆化搜索。

---

引例代码实现

我们的代码实现分为三步：

• 状态初始化
• 数位初始化
• 记忆化搜索

状态初始化

初始化f数组为-1，代表未访问过

int d[N] {0}, cnt;
int f[N][N] {0}; // 剩余i位，上一位为j

int dfs(int n, int pre, bool lim) {
    //……
}

int nondec(int x) {
	//……
}

int main() {
	//……
    memset(f, -1, sizeof(f));
	//……
    return 0;
}

数位初始化

即将给定数字x的各个数位上的数字存储到对应下标数组之中。

int nondec(int x) {
    cnt = 0;

    while (x)
        d[++cnt] = x % 10, x /= 10;

    return dfs(cnt, 0, false);
}

记忆化搜索

记忆化搜索也是我们的核心代码，如下：

int dfs(int n, int pre, bool lim) {
    if (n == 0)
        return 1;								//(1)

    if (lim && ~f[n][pre])
        return f[n][pre];						 //(2)

    int res = 0, ceil = lim ? 9 : d[n];			  //(3)

    for (int i = pre; i <= ceil; i++)
        res += dfs(n - 1, i, lim || i < ceil);	   //(4)

    if (lim)
        f[n][pre] = res;					     //(5)

    return res;
}

对于dfs函数可以划分为5块：

1. n = 0时的递归出口，每个数位都已经枚举完毕，能进入函数，说明满足不降数，直接返回1
2. 如果lim = true（我们递归树剪枝的那一部分），并且已经访问过，那么直接访问保存的状态
3. 根据lim来求枚举数位的上限ceil，如果lim为真，那么上限就是进制减一，这里对应十进制那么就是9，否则上限就是对应数位d[n]
4. 递归到子问题，根据枚举数位，传入新状态和新lim
5. 如果lim为true，那么我们进行记忆化搜索，剪枝

---

非递归如何实现？

即然能用递归求解，自然也有相应的递推解法，递推解法无非就是自下而上的求解过程。

仍以引例-不降数为例。我们状态定义仍为f[n][pre]代表n位，上一位为pre时的不降数数目，则仍有状态转移方程：
$$f[n][pre]=\sum _{k=pre}^{ceil}f[n?1][k]$$
但是我们发现，如果按照记忆化搜索的初始化方法，我们是无法得到正确答案的，所以对于数位dp而言，记忆化搜索和递推解法思想类似，但是实现方法还是有一定差异的。

状态设计

定义状态f[i][j]为一共有i位，最高位为j的不降数的数目，这跟记忆化搜索的状态定义十分相似。

也可以使用和记忆化搜索一样的状态定义，但是修改下状态定义实现更为方便。

状态转移

$$f[i][j]=\sum _{k=j}^{9}f[i?1][k]$$

很好理解，对于最高位为j，它的下一位就必须从j开始，我们发现这里的上限直接给了9，而非ceil，是因为我们状态定义中不像记忆化搜索解法中那样与lim和pre强相关，而是朴素的对应位长和最高位的不降数的数目。

算法原理

对于不超过x的不降数数目，可以根据数位进行拆解：
$$nondec(x)=\sum _{i=0}^{d[n]?1}f[n][i]+\sum _{i=d[n]}^{d[n?1]?1}f[n?1][i]+\sum _{i=d[n?1]}^{d[n?2]?1}f[n?2][i]+\dots \dots$$
解释：我们仍按照数位从高到低进行枚举，如果第n位（最高位）小于d[n]对应的不降数显然都小于x，如果第n位等于d[n]，那么对应的不降数中有部分可能大于x，所以只能加上其中小于等于x的部分，为了保证小于等于x，我们以第n位为d[n]第二位从d[n]开始枚举，依次类推……

算法实现

初始化

#define N 15
int f[N][N]{0}; // 一共有i位。最高位为j的不降数个数
void init()
{
    for (int i = 0; i < 10; i++)
        f[1][i] = 1;
    for (int i = 2; i < N; i++)
        for (int j = 0; j <= 9; j++)
            for (int k = j; k <= 9; k++)
                f[i][j] += f[i - 1][k];
}

递推求解

把递推公式翻译成代码，从高位开始枚举，每次枚举的下限为上一位数字上限pre

int nondec(int x)
{
    if (!x)
        return 1;
    cnt = 0;
    while (x)
        d[++cnt] = x % 10, x /= 10;

    int res = 0, pre = 0;
    for (int i = cnt; i >= 1; i--)
    {
        int now = d[i];
        for (int j = pre; j < now; j++)
            res += f[i][j];

        if (now < pre)
            break;
        pre = now;
        if (i == 1)
            res++;
    }
    return res;
}

---

OJ精讲

Good Numbers

Problem - 4722 (hdu.edu.cn)

这里好数的定义为各个数位之和为10，那么我们前缀状态仍然用一位数字即可表示，即已经枚举数位的和对10取余

n = 0递归出口则要进行条件判定，如果前缀状态为0才能返回1，否则返回0

其它和例题一模一样，所以说数位dp可以说是模板题，只在递归出口和状态设计有区别。

AC代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define int long long
#define N 20

int d[N], cnt, t, a, b, idx = 0;
int f[N][10]; // 剩余i位，上一位为j

int dfs(int n, int pre, bool lim)
{
    if (n == 0)
        return !pre;
    if (lim && ~f[n][pre])
        return f[n][pre];

    int res = 0, ceil = lim ? 9 : d[n];
    for (int i = 0; i <= ceil; i++)
        res += dfs(n - 1, (i + pre) % 10, lim || i < d[n]);

    if (lim)
        f[n][pre] = res;
    return res;
}

int goodnum(int x)
{
    cnt = 0;
    while (x)
        d[++cnt] = x % 10, x /= 10;

    return dfs(cnt, 0, false);
}

signed main()
{
    // ios::sync_with_stdio(false);
    // cin.tie(nullptr), cout.tie(nullptr);
    // freopen("in.txt", "r", stdin);
    // freopen("out.txt", "w", stdout);
    memset(f, -1, sizeof(f));

    scanf("%lld", &t);

    while (t--)
    {
        scanf("%lld%lld", &a, &b);
        int ans = goodnum(b) - goodnum(a - 1);
        printf("Case #%lld: %lld\n", ++idx, ans);
    }
    return 0;
}

---

不要62

Problem - 2089 (hdu.edu.cn)

这个问题我们发现要求数字不能有4或者62数对，限制条件变成了两个，我们可以用三位十进制数字来表示前缀状态，但是其实没有必要，因为对于非法状态也就是非目标数字，我们直接停止递归返回0即可，所以我们仍然用一位存储状态，即上一位数字。

这就要求我们需要设计一个非法状态用来进行标记，非法直接退出递归。

为了代码简洁以及可读，我们把获取状态的代码段封装一下，其它和例题一样

我们发现数位dp不同题目只有前缀状态设计的差别和递归出口的细微差别

AC代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define int long long
#define N 11
int inf = -123456;
int d[N], cnt, t, a, b, idx = 0;
int f[N][10]; // 剩余i位，上一位为j

int getnxt(int pre, int digit)
{
    if (pre == inf || digit == 4 || (pre == 6 && digit == 2))
        return inf;
    return digit;
}

int dfs(int n, int pre, bool lim)
{
    if (pre == inf)
        return 0;
    if (n == 0)
        return 1;

    if (lim && ~f[n][pre])
        return f[n][pre];

    int res = 0, ceil = lim ? 9 : d[n];
    for (int i = 0; i <= ceil; i++)
    {
        res += dfs(n - 1, getnxt(pre, i), lim || i < d[n]);
    }
    if (lim)
        f[n][pre] = res;
    return res;
}

int goodnum(int x)
{
    cnt = 0;
    while (x)
        d[++cnt] = x % 10, x /= 10;

    return dfs(cnt, 0, false);
}

signed main()
{
    // ios::sync_with_stdio(false);
    // cin.tie(nullptr), cout.tie(nullptr);
    // freopen("in.txt", "r", stdin);
    // freopen("out.txt", "w", stdout);
    memset(f, -1, sizeof(f));

    while (cin >> a >> b, a || b)
    {
        cout << goodnum(b) - goodnum(a - 1) << '\n';
    }
    return 0;
}

---

不含连续1的非负整数

600. 不含连续1的非负整数

有没有感觉leetcode上的hard题目竟然显得如此简单

目标数字不能含连续1，那么我们仍然用一位来保存前缀状态，我们只对合法状态进行递归即可，很简单的啦

AC代码

int f[32][32] , d[32] , cnt = 0;
class Solution {
public:
    Solution()
    {memset(f , -1 , sizeof(f));}
    int dfs(int n , int pre , bool lim)
    {
        if(!n) return 1;
        if(lim && ~f[n][pre]) return f[n][pre];
        int ceil = lim ? 1 : d[n];
        int res = 0;
        for(int i = 0 ; i <= ceil ; i++)
            if(pre == 1 && i == 1) continue;
            else res += dfs(n - 1 , i , lim || i < ceil);
        if(lim)
        f[n][pre] = res;
        return res;
    }
    int getnum(int x)
    {
        cnt = 0;
        while(x) d[++cnt] = x % 2 , x /= 2;
        return dfs(cnt , 0 , false);
    }
    int findIntegers(int n) {
        return getnum(n);
    }
};

---

总结

数位dp其实是一种少状态数状态机dp，不同题目可以用一套模板解决，但是要注意前缀状态的设计和递归出口的处理。