数据结构与算法（六）

高频-体系学习班（六）

41 四边形不等式技巧（上）

• 内容：
  • 区间划分问题中的划分点不回退现象
  • 四边形不等式技巧特征
    • 1、两个可变参数的区间划分问题
    • 2、每个格子有枚举行为
    • 3、当两个可变参数固定一个，另一个参数和答案之间存在单调性关系
    • 4、而且两组单调关系是反向的：(升 升，降 降) (升 降，降 升)
    • 5、能否获得指导枚举优化的位置对：上+右，或者，左+下
    • 6、不要证明！用对数器验证！
    • 7、可以把时间复杂度降低一阶
  • 四边形不等式技巧注意点
    • 1、不要证明！用对数器验证！
    • 2、枚举的时候面对最优答案相等的时候怎么处理？用对数器都试试！
    • 3、可以把时间复杂度降低一阶
      • O(N^3) -> O(N^2)
      • O(N^2 * M) -> O(N * M)
      • O(N * M^2) -> O(N * M)
    • 4、四边形不等式有些时候是最优解，有些时候不是
      • 不是的原因：尝试思路，在根儿上不够好

41.1 非负数组切分成左右两部分累加和的最大值

• 给定一个非负数组arr，长度为N，那么有N-1种方案可以把arr切成左右两部分。每一种方案都有，min{左部分累加和，右部分累加和}。求这么多方案中，min{左部分累加和，右部分累加和}的最大值是多少？整个过程要求时间复杂度O(N)。
• 方法一：暴力解，时间复杂度 O(N^2)

public static int bestSplit0(int[] arr) {
   
	if (arr == null || arr.length < 2) return 0;
	int ans = 0, n = arr.length;
	// 长度n数组有n-1种划分方式
	for (int i = 0; i < n - 1; i++) {
   
		// 分别计算每一种划分方式下的左右两部分的累加和
		int sumL = 0, sumR = 0;
		for (int l = 0; l <= i; l++) sumL += arr[l];
		for (int r = i + 1; r < n; r++) sumR += arr[r];
		// 收集答案
		ans = Math.max(ans, Math.min(sumL, sumR));
	}
	return ans;
}

• 方法二：使用预处理数组累加和，时间复杂度O(N)

public static int bestSplit(int[] arr) {
   
	if (arr == null || arr.length < 2) return 0;
	// 先预处理计算出整个数组的累加和
	int n = arr.length, sum = 0, ans = 0, sumL = 0;
	for (int x : arr) sum += x;
	// 依次遍历每一种划分方式，计算左部分累加和、右部分累加和 = 总累加和 - 左部分累加和
	for (int i = 0; i < n - 1; i++) {
   
		sumL += arr[i];
		ans = Math.max(ans, Math.min(sumL, sum - sumL));
	}
	return ans;
}

41.2 非负数组切分成左右两部分累加和的最大值的数组

• 把题目一中提到的，min{左部分累加和，右部分累加和}，定义为S(N-1)，也就是说：S(N-1)：在arr[0…N-1]范围上，做最优划分所得到的min{左部分累加和，右部分累加和}的最大值。现在要求返回一个长度为 N 的s数组，s[i] =在arr[0…i]范围上，做最优划分所得到的min{左部分累加和，右部分累加和}的最大值，得到整个s数组的过程，做到时间复杂度O(N)。
• 方法一：暴力解，时间复杂度 O(N^3)

public static int[] bestSplit0(int[] arr) {
   
	if (arr == null || arr.length == 0) return new int[0];
	int n = arr.length;
	int[] ans = new int[n];
	for (int range = 1; range < n; range++) {
   
		for (int i = 0; i < range; i++) {
   
			int sumL = 0, sumR = 0;
			for (int l = 0; l <= i; l++) sumL += arr[l];
			for (int r = i + 1; r <= range; r++) sumR += arr[r];
			ans[range] = Math.max(ans[range], Math.min(sumL, sumR));
		}
	}
	return ans;
}

• 方法二：利用预处理前缀和数组优化，时间复杂度O(N^2)

public static int[] bestSplit(int[] arr) {
   
	if (arr == null || arr.length == 0) return new int[0];
	int n = arr.length;
	int[] ans = new int[n], sum = new int[n + 1];
	for (int i = 0; i < n; i++) sum[i + 1] = sum[i] + arr[i];
	for (int range = 1; range < n; range++) {
   
		for (int i = 0; i < range; i++) {
   
			int sumL = rangeSum(sum, 0, i), sumR = rangeSum(sum, i + 1, range);
			ans[range] = Math.max(ans[range], Math.min(sumL, sumR));
		}
	}
	return ans;
}
private static int rangeSum(int[] sum, int l, int r) {
   
	return sum[r + 1] - sum[l];
}

• 结论：当 s[i] 时最优划分位置如果是 x，那么当来到 s[i + 1] 时最优划分位置一定不会出现在 x 的左侧（不回退）
• 方法三：最优解，时间复杂度O(N)
  • ans = max{ min{左部分累加和，右部分累加和} }，存在不回退情况
  • 进一步抽象化：
    • ans = 最优{ 最差{左部分指标，右部分指标} }，可能存在不回退情况
    • ans = 最差{ 最优{左部分指标，右部分指标} }，也可能存在不回退情况
    • !!!注意：这个指标应该要和这个数组的区间存在单调性

public static int[] bestSplitOptimal(int[] arr) {
   
	if (arr == null || arr.length == 0) return new int[0];
	int n = arr.length;
	int[] ans = new int[n], sum = new int[n + 1];
	for (int i = 0; i < n; i++) sum[i + 1] = sum[i] + arr[i];
	// 最优划分 0~range-1上，最优划分是左部分[0, best]  右部分[best+1, range-1]
	int best = 0;
	for (int range = 1; range < n; range++) {
   
		while (best + 1 < range) {
   
			int before = Math.min(rangeSum(sum, 0, best), rangeSum(sum, best + 1, range));
			int after = Math.min(rangeSum(sum, 0, best + 1), rangeSum(sum, best + 2, range));
			if (after >= before) best++;
			else break;
		}
		ans[range] = Math.min(rangeSum(sum, 0, best), rangeSum(sum, best + 1, range));
	}
	return ans;
}

41.3 合并石子的得分

• 摆放着n堆石子，现要将石子有次序地合并成一堆，规定每次只能选相邻的2堆石子合并成新的一堆。并将新的一堆石子数记为该次合并的得分，求出将n堆石子合并成一堆的最小得分（或最大得分）合并方案。
• 方法一：前缀和优化区间和计算+暴力递归

public static int minStoneMerge0(int[] arr) {
   
    if (arr == null || arr.length < 2) return 0;
    int[] sum = getPrefixSum(arr);
    return process(sum, 0, arr.length - 1);
}
// 返回 l~r 范围进行相邻石子合并得分的最小值
private static int process(int[] sum, int l, int r) {
   
    if (l == r) return 0;
    int next = Integer.MAX_VALUE;
    for (int leftEnd = l; leftEnd < r; leftEnd++) {
   
        next = Math.min(next, process(sum, l, leftEnd) + process(sum, leftEnd + 1, r));
    }
    return next + rangeSum(sum, l, r);
}
// 前缀和数组
private static int[] getPrefixSum(int[] arr) {
   
    int n = arr.length;
    int[] sum = new int[n + 1];
    for (int i = 0; i < n; i++) sum[i + 1] = sum[i] + arr[i];
    return sum;
}
// 区间和
private static int rangeSum(int[] sum, int l, int r) {
   
    return sum[r + 1] - sum[l];
}

• 方法二：动态规划，存在枚举划分位置，时间复杂度 O(N^3)

public static int minStoneMerge(int[] arr) {
   
    if (arr == null || arr.length < 2) return 0;
    int n = arr.length;
    int[] sum = getPrefixSum(arr);
    int[][] dp = new int[n][n];
    // 左下半边区域无效，对角线 dp[i][i] = 0;
    // 整体从下至上(n-2 ~ 0)，从左至右(l ~ n) 填写dp表
    for (int l = n - 2; l >= 0; l--) {
   
        for (int r = l + 1; r < n; r++) {
   
            int next = Integer.MAX_VALUE;
            // 枚举每一个划分位置
            for (int leftEnd = l; leftEnd < r; leftEnd++) {
   
                next = Math.min(next, dp[l][leftEnd] + dp[leftEnd + 1][r]);
            }
            dp[l][r] = next + rangeSum(sum, l, r);
        }
    }
    return dp[0][n - 1];
}

• 方法三：四边形不等式优化-动态规划，时间复杂度 O(N^2)

public static int minStoneMergeOptimal(int[] arr) {
   
    if (arr == null || arr.length < 2) return 0;
    int n = arr.length;
    int[] sum = getPrefixSum(arr);
    // best: 记录取得最优划分点的位置
    int[][] dp = new int[n][n], best = new int[n][n];
    // 填写倒数第2条斜对角线的dp表和best表
    for (int i = 0; i < n - 1; i++) {
   
        best[i][i + 1] = i;
        dp[i][i + 1] = rangeSum(sum, i, i + 1);
    }
    for (int l = n - 3; l >= 0; l--) {
   
        for (int r = l + 2; r < n; r++) {
   
            int next = Integer.MAX_VALUE, choose = -1;
            // 针对方法二`枚举每一个划分位置`进行优化: 利用best数组限制leftEnd的边界(左边, 下边)
            for (int leftEnd = best[l][r - 1]; leftEnd <= best[l + 1][r]; leftEnd++) {
   
                int cur = dp[l][leftEnd] + dp[leftEnd + 1][r];
                if (cur <= next) {
   
                    next = cur;
                    // 记下此时取得最优的位置
                    choose = leftEnd;
                }
            }
            best[l][r] = choose;
            dp[l][r] = next + rangeSum(sum, l, r);
        }
    }
    return dp[0][n - 1];
}

41.4 画匠问题

• 给定一个整型数组 arr，数组中的每个值都为正数，表示完成一幅画作需要的时间，再给定一个整数num，表示画匠的数量，每个画匠只能画连在一起的画作。所有的画家并行工作，返回完成所有的画作需要的最少时间。

  • 例1：arr=[3,1,4]，num=2，最好的分配方式为第一个画匠画3和1，所需时间为4；第二个画匠画4，所需时间为4，所以返回4。
  • 例2：arr=[1,1,1,4,3]，num=3，最好的分配方式为第一个画匠画前三个1，所需时间为3；第二个画匠画4，所需时间为4；第三个画匠画3，所需时间为3，返回4。

• 测试链接：https://leetcode.cn/problems/split-array-largest-sum/

• 方法一：不优化枚举的动态规划方法，时间复杂度O(N^2 * K)

public static int splitArray(int[] nums, int k) {
   
	int n = nums.length;
	int[] sum = getPrefixSum(nums);
	// dp[i][j]: 0~i幅画交给j个画匠完成的最短时间
	int[][] dp = new int[n][k + 1];
	// 初始化dp表，第0列(没有画匠)无效
	// 第0行: 0~0，很显然一幅画，最短时间就是nums[0]
	for (int j = 1; j <= k; j++) dp[0][j] = nums[0];
	// 第1列: 很显然1个画匠完成0~i幅画，最短时间就是arr[0...i]累加和
	for (int i = 1; i < n; i++) dp[i][1] = rangeSum(sum, 0, i);
	// 其它位置: 从上往下、从左往右 递推
	for (int i = 1; i < n; i++) {
   
		for (int j = 2; j <= k; j++) {
   
			int ans = Integer.MAX_VALUE;
			// 枚举每一个划分位置(不进行优化)
			for (int leftEnd = 0; leftEnd < i; leftEnd++) {
   
				ans = Math.min(ans, Math.max(dp[leftEnd][j - 1], rangeSum(sum, leftEnd + 1, i)));
			}
			dp[i][j] = ans;
		}
	}
	return dp[n - 1][k];
}
// 前缀和数组
private static int[] getPrefixSum(int[] arr) {
   
    int n = arr.length;
    int[] sum = new int[n + 1];
    for (int i = 0; i < n; i++) sum[i + 1] = sum[i] + arr[i];
    return sum;
}
// 区间和
private static int rangeSum(int[] sum, int l, int r) {
   
    return sum[r + 1] - sum[l];
}

• 方法二：使用四边形不等式优化枚举-动态规划，时间复杂度O(N * K)

public static int splitArray(int[] nums, int k) {
   
	int n = nums.length;
	int[] sum = getPrefixSum(nums);
	// best: 记录取得最优划分点的位置
	int[][] dp = new int[n][k + 1], best = new int[n][k + 1];
	// 初始化dp表，第0列(没有画匠)无效
	// 第0行: 0~0，很显然一幅画，最短时间就是nums[0]，最优划分点 -1
	for (int j = 1; j <= k; j++) {
   
		dp[0][j] = nums[0];
		best[0][j] = -1;
	}
	// 第1列: 很显然1个画匠完成0~i幅画，最短时间就是arr[0...i]累加和，最优划分点 -1
	for (int i = 1; i < n; i++) {
   
		dp[i][1] = rangeSum(sum, 0, i);
		best[i][1] = -1;
	}
	// 其它位置: 从左往右、从下往上 递推
	// 为什么这样的顺序？因为要去凑（左，下）优化位置对儿！
	for (int j = 2; j <= k; j++) {
   
		for (int i = n - 1; i >= 1; i--) {
   
			int ans = Integer.MAX_VALUE, bestChoose = -1;
			// 如果i==N-1，则不优化上限
			int down = best[i][j - 1], up = i == n - 1 ? n - 1 : best[i + 1][j];
			// 使用四边形不等式优化枚举位置
			for (int leftEnd = down; leftEnd <= up; leftEnd++) {
   
				int leftCost = leftEnd == -1 ? 0 : dp[leftEnd][j - 1];
				int rightCost = leftEnd == i ? 0 : rangeSum(sum, leftEnd + 1, i);
				int cur = Math.max(leftCost, rightCost);
				/**
				 * 注意下面的if一定是 < 课上的错误就是此处！当时写的 <=
				 * 也就是说，只有取得明显的好处才移动，举个例子来说明，比如[2,6,4,4]，3个画匠时候，如下两种方案都是最优
				 * (2,6) (4) 两个画匠负责 | (4) 最后一个画匠负责；(2,6) (4,4)两个画匠负责 | 最后一个画匠什么也不负责
				 * 第一种方案划分为：[0~2] [3~3]；第二种方案划分为：[0~3] [无]
				 * 两种方案的答案都是8，但是划分点位置一定不要移动，只有明显取得好处时(<)，划分点位置才移动
				 * 也就是说后面的方案如果==前面的最优，不要移动！只有优于前面的最优，才移动
				 * 比如上面的两个方案，如果你移动到了方案二，你会得到：[2,6,4,4] 三个画匠时，最优为[0~3](前两个画家) [无](最后一个画家)，
				 * 最优划分点为3位置(best[3][3])，那么当4个画匠时，也就是求解dp[3][4]时，因为best[3][3] = 3，这个值提供了dp[3][4]的下限
				 * 而事实上dp[3][4]的最优划分为：[0~2]（三个画家处理） [3~3] (一个画家处理)，此时最优解为6
				 * 所以，你就得不到dp[3][4]的最优解了，因为划分点已经越过2了
				 * 提供了对数器验证，你可以改成<=，对数器和leetcode都过不了，这里是<，对数器和leetcode都能通过
				 * 这里面会让同学们感到困惑的点：为啥==的时候，不移动，只有<的时候，才移动呢？例子懂了，但是道理何在？
				 * 哈哈哈哈哈，看了邮局选址问题，你更懵，请看42节！
				 */
				if (cur < ans) {
   
					ans = cur;
					bestChoose = leftEnd;
				}
			}
			dp[i][j] = ans;
			best[i][j] = bestChoose;
		}
	}
	return dp[n - 1][k];
}

• 方法三：最优解，O(N) 以画匠数量作为二分的目标

public static int splitArrayOptimal(int[] nums, int k) {
   
	// 先计算nums数组的累加和
	long sum = 0;
	for (int x : nums) sum += x;
	// 在0~sum上做二分
	long l = 0, r = sum, mid, cur, ans = 0;
	while (l <= r) {
   
		mid = (l + r) / 2;
		cur = getNeedParts(nums, mid);
		if (cur <= k) {
   
			ans = mid;
			r = mid - 1;
		} else l = mid + 1;
	}
	return (int) ans;
}
// 达成目标aim时，返回至少需要几个画匠
private static int getNeedParts(int[] nums, long aim) {
   
	for (int x : nums) {
   
		if (x > aim) return Integer.MAX_VALUE;
	}
	int ans = 1, sum = nums[0];
	for (int i = 1; i < nums.length; i++) {
   
		// 如果超了目标aim，就新加一个画匠，否则累加到sum
		if (sum + nums[i] > aim) {
   
			ans++;
			sum = nums[i];
		} else sum += nums[i];
	}
	return ans;
}

42 四边形不等式技巧（下）

• 内容：
  • 继续熟悉四边形不等式
  • 展示好的尝试是最关键的

42.1 邮局选址问题

• 一条直线上有居民点，邮局只能建在居民点上。给定一个有序正数数组arr，每个值表示居民点的一维坐标，再给定一个正数 num，表示邮局数量。选择num个居民点建立num个邮局，使所有的居民点到最近邮局的总距离最短，返回最短的总距离。
  • 例如：arr=[1,2,3,4,5,1000]，num=2，第一个邮局建立在3位置，第二个邮局建立在1000位置，那么1位置到邮局的距离为2，2位置到邮局距离为1，3位置到邮局的距离为0，4位置到邮局的距离为1，5位置到邮局的距离为2，1000位置到邮局的距离为0。这种方案下的总距离为6，其他任何方案的总距离都不会比该方案的总距离更短，所以返回6。

预处理一个结构：一张 w 表，w[i][j] 返回 [i, j] （i < j）范围只建一个邮件时的最短距离。

结论：在一个有序数组中，如果只建一个邮件，那么选择中点（奇数：中点、偶数：上中点或下中点都行）位置一定是最优的。（不用管数据多么倾斜）

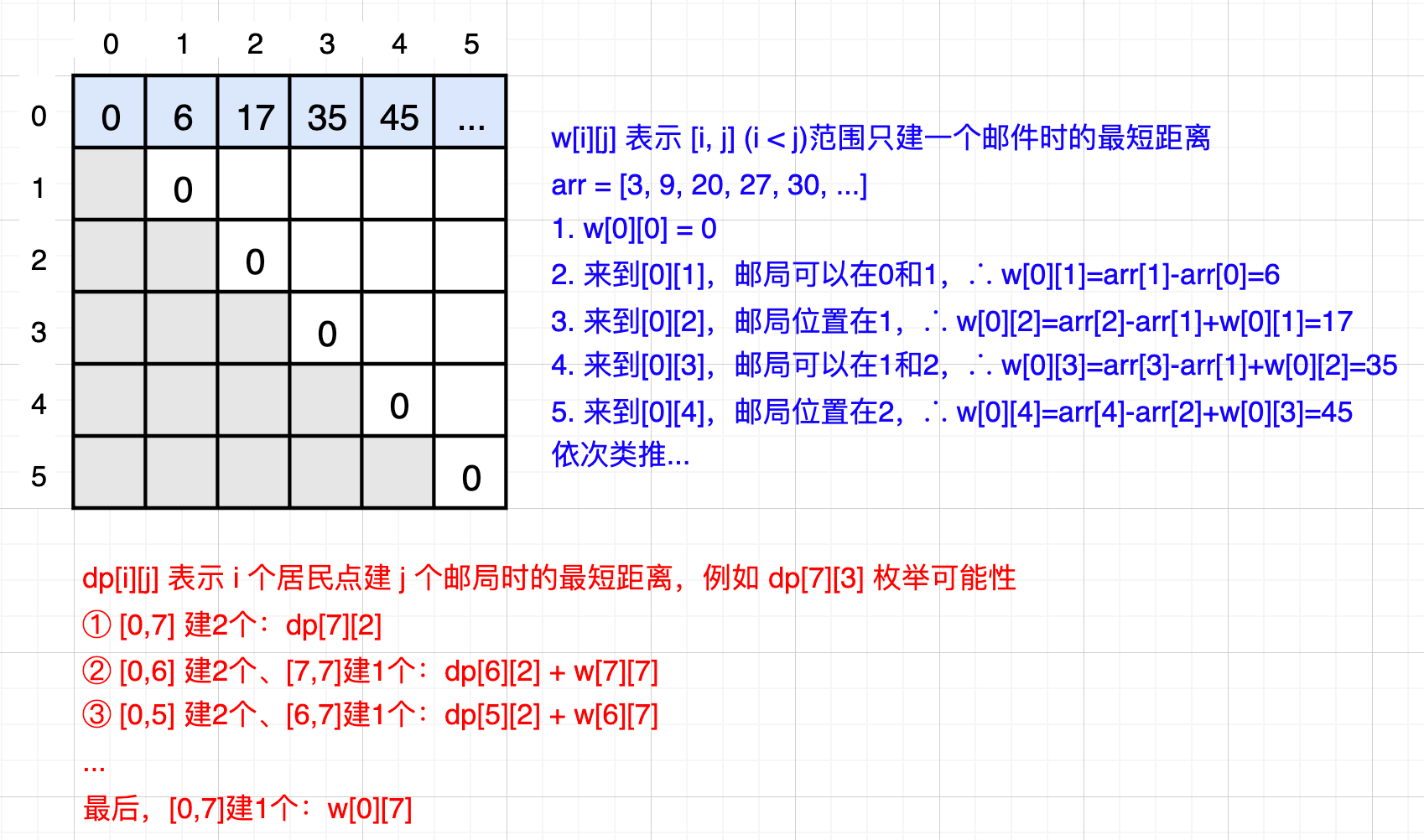
• 方法一：不优化版本的动态规划

public static int minDistance(int[] arr, int num) {
   
	if (arr == null || arr.length < num || num < 1) return 0;
	int n = arr.length;
	// 预处理结构：w[i][j] 返回 [i, j] （i < j）范围只建一个邮件时的最短距离
	// w多准备一个长度，避免边界值处理
	int[][] w = new int[n + 1][n + 1];
	// 初始化w数组，只填右上半区域（从上往下、从左往右）
	for (int i = 0; i < n; i++) {
   
		for (int j = i + 1; j < n; j++) {
   
			w[i][j] = w[i][j - 1] + (arr[j] - arr[(i + j) >> 1]);
		}
	}
	int[][] dp = new int[n][num + 1];
	// 初始化dp数组，第0行(即0个居民点，显然都是0，不用填)，第0列(即0个邮件，无效不用填)
	// 第1列直接从w数组拿值
	for (int i = 0; i < n; i++) dp[i][1] = w[0][i];
	for (int i = 1; i < n; i++) {
   
		// 优化 Math.min(i, num)，即邮件点个数如果超过居民点个数，最短距离一定是0(每个居民点都可以建一个邮件)，不用求
		for (int j = 2; j <= Math.min(i, num); j++) {
   
			int ans =  Integer.MAX_VALUE;
			// 不做优化，枚举每一个划分位置
			for (int k = 0; k <= i; k++) {
   
				ans = Math.min(ans, dp[k][j - 1] + w[k + 1][i]);
			}
			dp[i][j] = ans;
		}
	}
	return dp[n - 1][num];
}

• 方法二：优化枚举行为版本的动态规划

public static int minDistanceOptimal(int[] arr, int num) {
   
	if (arr == null || arr.length < num || num < 1) return 0;
	int n = arr.length;
	// 预处理结构：w[i][j] 返回 [i, j] （i < j）范围只建一个邮件时的最短距离
	// w多准备一个长度，避免边界值处理
	int[][] w = new int[n + 1][n + 1];
	// 初始化w数组，只填右上半区域（从上往下、从左往右）
	for (int i = 0; i < n; i++) {
   
		for (int j = i + 1; j < n; j++) {
   
			w[i][j] = w[i][j - 1] + (arr[j] - arr[(i + j) >> 1]);
		}
	}
	int[][] dp = new int[n][num + 1];
	int[][] best = new int[n][num + 1];
	// 初始化dp数组，第0行(即0个居民点，显然都是0，不用填)，第0列(即0个邮件，无效不用填)
	// 第1列直接从w数组拿值
	for (int i = 0; i < n; i++) {
   
		dp[i][1] = w[0][i];
		best[i][1] = -1;
	}
	for (int j = 2; j <= num; j++) {
   
		for (int i = n - 1; i >= j; i--) {
   
			int down = best[i][j - 1], up = i == n - 1 ? n - 1 : best[i + 1][j];
			int ans = Integer.MAX_VALUE, bestChoose = -1;
			for (int leftEnd = down; leftEnd <= up; leftEnd++) {
   
				int leftCost = leftEnd == -1 ? 0 : dp[leftEnd][j - 1];
				int rightCost = leftEnd == i ? 0 : w[leftEnd + 1][i];
				int cur = leftCost + rightCost;
				// 这里 <= 或 < 都对
				if (cur <= ans) {
   
					ans = cur;
					bestChoose = leftEnd;
				}
			}
			dp[i][j] = ans;
			best[i][j] = bestChoose;
		}
	}
	return dp[n - 1][num];
}

42.2 丢棋子问题

• 一座大楼有0~N层，地面算作第0层，最高的一层为第N层。已知棋子从第0层掉落肯定不会摔碎，从第i层掉落可能会摔碎，也可能不会摔碎(1≤i≤N)。给定整数N作为楼层数，再给定整数K作为棋子数，返回如果想找到棋子不会摔碎的最高层数，即使在最差的情况下扔的最少次数，一次只能扔一个棋子。
  • 例1：N=10，K=1，返回10。因为只有1棵棋子，所以不得不从第1层开始一直试到第10层，在最差的情况下，即第10层是不会摔坏的最高层，最少也要扔10次。
  • 例2：N=3，K=2，返回2。先在2层扔1棵棋子，如果碎了试第1层，如果没碎试第3层。
  • 例3：N=105，K=2，返回14。
    • 第一个棋子先在14层扔，碎了则用仅存的一个棋子试1~13；
    • 若没碎，第一个棋子继续在27层扔，碎了则用仅存的一个棋子试15~26
    • 若没碎，第一个棋子继续在39层扔，碎了则用仅存的一个棋子试28~38
    • 若没碎，第一个棋子继续在50层扔，碎了则用仅存的一个棋子试40~49
    • 若没碎，第一个棋子继续在60层扔，碎了则用仅存的一个棋子试51~59
    • 若没碎，第一个棋子继续在69层扔，碎了则用仅存的一个棋子试61~68
    • 若没碎，第一个棋子继续在77层扔，碎了则用仅存的一个棋子试70~76
    • 若没碎，第一个棋子继续在84层扔，碎了则用仅存的一个棋子试78~83
    • 若没碎，第一个棋子继续在90层扔，碎了则用仅存的一个棋子试85~89
    • 若没碎，第一个棋子继续在95层扔，碎了则用仅存的一个棋子试91~94
    • 若没碎，第一个棋子继续在99层扔，碎了则用仅存的一个棋子试96~98
    • 若没碎，第一个棋子继续在102层扔，碎了则用仅存的一个棋子试100、101
    • 若没碎，第一个棋子继续在104层扔，碎了则用仅存的一个棋子试103
    • 若没碎，第一个棋子继续在105层扔，若到这一步还没碎，那么105便是结果
• 方法一：暴力递归，复杂度太高会超时

public static int superEggDrop0(int k, int n) {
   
	if (k < 1 || n < 1) return 0;
	return process(n, k);
}
// 还剩k个鸡蛋去验证level层楼，返回至少需要扔几次
private static int process(int level, int k) {
   
	if (level == 0) return 0;
	// 只有1个鸡蛋时，只能依次从下往上每层楼都去试
	if (k == 1) return level;
	int min = Integer.MAX_VALUE;
	for (int i = 1; i <= level; i++) {
   
		// 1、第i层鸡蛋碎了，则还剩k-1个鸡蛋去下面的i-1层尝试
		// 2、第i层鸡蛋没碎，则还剩k个鸡蛋去上面的level-i层尝试
		min = Math.min(min, Math.max(process(i - 1, k - 1), process(level - i, k)));
	}
	return min + 1;
}

• 方法二：改动态规划(不进行枚举优化)，复杂度还是太高会超时

public static int superEggDrop(int k, int n) {
   
	if (k < 1 || n < 1) return 0;
	if (k == 1) return n;
	// dp[i][j]: i层楼有j个鸡蛋最多扔几次
	int[][] dp = new int[n + 1][k + 1];
	// 初始化dp，第0行(即0层楼不用尝试)都是0，第0列(即0个鸡蛋)无效
	// 第1列(即1个鸡蛋，则最差情况有多少层楼就得尝试多少次)
	for (int i = 1; i <= n; i++) dp[i][1] = i;
	// 普遍位置填写dp表，从上往下、从左往右
	for (int i = 1; i <= n; i++) {
   
		for (int j = 2; j <= k; j++) {
   
			int min = Integer.MAX_VALUE;
			// 枚举每一种情况
			for (int i0 = 1; i0 <= i; i0++) {
   
				min = Math.min(min, Math.max(dp[i0 - 1][j - 1], dp[i - i0][j]));
			}
			dp[i][j] = min + 1;
		}
	}
	return dp[n][k];
}

• 方法三：进行四边形不等式枚举优化版本的动态规划，能勉强通过

public static int superEggDropOptimize(int k, int n) {
   
	if (k < 1 || n < 1) return 0;
	if (k == 1) return n;
	// dp[i][j]: i层楼有j个鸡蛋最多扔几次
	int[][] dp = new int[n + 1][k + 1];
	int[][] best = new int[n + 1][k + 1];
	// 初始化dp，第0行(即0层楼不用尝试)都是0，第0列(即0个鸡蛋)无效
	// 第1列(即1个鸡蛋，则最差情况有多少层楼就得尝试多少次)
	for (int i = 1; i <= n; i++) dp[i][1] = i;
	// 第1行(即1层楼，不管有几个鸡蛋都只需要尝试1次)
	for (int i = 1; i <= k; i++) {
   
		dp[1][i] = 1;
		best[1][i] = 1;
	}
	// 普遍位置填写dp表，从上往下、从右往左
	for (int i = 2; i <= n; i++) {
   
		for (int j = k; j > 1; j--) {
   
			// 依赖上边作为下限、右边作为上限
			int down = best[i - 1][j], up = j == k ? i : best[i][j + 1];
			int min =