wy的leetcode刷题记录_Day72

wy的leetcode刷题记录_Day72

声明

本文章的所有题目信息都来源于leetcode
如有侵权请联系我删掉!
时间：

前言

2397. 被列覆盖的最多行数

今天的每日一题是：2397. 被列覆盖的最多行数

题目介绍

给你一个下标从 0 开始、大小为 m x n 的二进制矩阵 matrix ；另给你一个整数 numSelect，表示你必须从 matrix 中选择的 不同 列的数量。

如果一行中所有的 1 都被你选中的列所覆盖，则认为这一行被 覆盖 了。

形式上，假设 s = {c1, c2, …, cnumSelect} 是你选择的列的集合。对于矩阵中的某一行 row ，如果满足下述条件，则认为这一行被集合 s 覆盖：

对于满足 matrix[row][col] == 1 的每个单元格 matrix[row][col]（0 <= col <= n - 1），col 均存在于 s 中，或者
row 中 不存在 值为 1 的单元格。
你需要从矩阵中选出 numSelect 个列，使集合覆盖的行数最大化。

返回一个整数，表示可以由 numSelect 列构成的集合 覆盖 的 最大行数 。

示例 1：

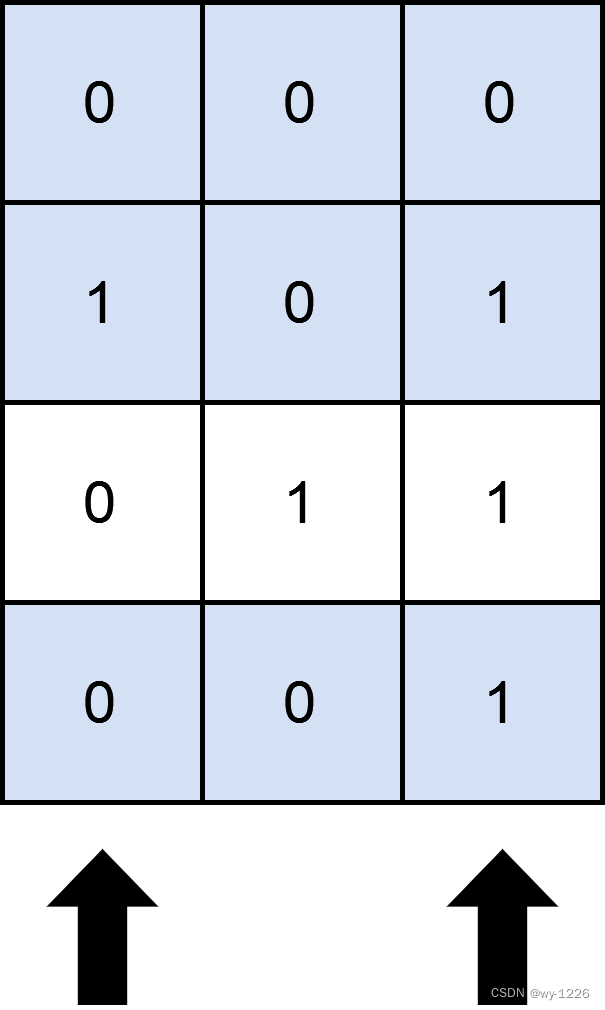
输入：matrix = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], numSelect = 2
输出：3
解释：
图示中显示了一种覆盖 3 行的可行办法。 选择 s = {0, 2} 。

• 第 0 行被覆盖，因为其中没有出现 1 。
• 第 1 行被覆盖，因为值为 1 的两列（即 0 和 2）均存在于 s 中。
• 第 2 行未被覆盖，因为 matrix[2][1] == 1 但是 1 未存在于 s 中。
• 第 3 行被覆盖，因为 matrix[2][2] == 1 且 2 存在于 s 中。 因此，可以覆盖 3 行。 另外 s = {1, 2} 也可以覆盖 3 行，但可以证明无法覆盖更多行。

示例 2：

输入：matrix = [[1],[0]], numSelect = 1
输出：2
解释：
选择唯一的一列，两行都被覆盖了，因为整个矩阵都被覆盖了。 所以我们返回 2 。

思路

暴力法解决：二进制枚举：使用二进制来表示每一行的1的分布情况以及搜寻情况，具体如下：使用mask[i]表示第i行中的1的分布情况，若mask[i]的二进制数位上为1其对应的矩阵中也为1。threshold用来表示当前遍历的选择列的情况，若threshold的二进制数位上为1则对应列被选中。

代码

class Solution {
public:
    int maximumRows(vector<vector<int>>& matrix, int numSelect) {

        int row=matrix.size();
        int col=matrix[0].size();
        vector<int> mask(row,0);//表示当前行中1的情况

        //初始化mask
        for(int i=0;i<row;i++)
        {
            for(int j=0;j<col;j++)
            {
                mask[i]+=matrix[i][j]<<(col-j-1);
            }
        }

        int curr=0;
        int ans=0;
        int threshold=(1<<col);
        for(int i=1;i<=threshold;i++)
        {
            curr=0;
            if(__builtin_popcount(i)!=numSelect)
            {
                continue;
            }
            for(int j=0;j<row;j++)
            {
                if((mask[j]&i)==mask[j])
                {
                    curr++;
                }
            }
            ans=max(curr,ans);
        }
        return ans;
    }
};

收获

通过使用二进制数可以表达的含义有很多可以简化很多操作。

1137. 第 N 个泰波那契数

1137. 第 N 个泰波那契数

题目介绍

泰波那契序列 Tn 定义如下：

T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2

给你整数 n，请返回第 n 个泰波那契数 Tn 的值。

示例 1：
输入：n = 4
输出：4
解释： T_3 = 0 + 1 + 1 = 2 T_4 = 1 + 1 + 2 = 4

示例 2：
输入：n = 25
输出：1389537

思路

其实这道题就是对斐波那契数列的一个重定义，只是递归条件增加，递归方程式需要改变一下即可。对于矩阵快速幂也是同理，重新梳理一下递推矩阵即可。

代码

递归（超时）：

class Solution {
public:
    int tribonacci(int n) {
        if(n<=1)
            return n;
        if(n==2)
            return 1;
        return tribonacci(n-1)+tribonacci(n-2)+tribonacci(n-3);
    }
};

递推（剩去了计算多余的fib数列）:

class Solution {
public:
    int tribonacci(int n) {
        if(n<=1)
            return n;
        if(n==2)
            return 1;
        int a=0;int b=1;int c=1;
        int ans=0;
        for(int i=3;i<=n;i++)
        {
           ans=a+b+c;
           a=b;
           b=c;
           c=ans; 
        }
        return ans;
    }
};

矩阵快速幂：

class Solution {
public:
            //矩阵乘法
    vector<vector<long>> martix_mutiply(vector<vector<long>> &a,vector<vector<long>>& b)
    {
        vector<vector<long>> c{{0,0,0},{0,0,0},{0,0,0}};
        for(int i=0;i<3;i++)
        {
            for(int j=0;j<3;j++)
            {
                c[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j]+a[i][2]*b[2][j];
            }
        }
        return c;
    }
    //快速幂
    vector<vector<long>> martix_rapid_pow(vector<vector<long>> &a,int n)
    {
        vector<vector<long>> ret{{1,0,0},{0,1,0},{0,0,1}};
        while(n>0)
        {
            if(n&1)
            {
                ret=martix_mutiply(ret,a);
            }
            n>>=1;
            a=martix_mutiply(a,a);
        }
        return ret;
    }

    int tribonacci(int n) {
        //矩阵快速幂
        if (n < 2) {
            return n;
        }
        vector<vector<long>> q{{1, 1,1}, {1, 0,0},{0,1,0}};
        vector<vector<long>> res = martix_rapid_pow(q, n - 1);
        return res[0][0];


    }

};

收获

重温矩阵快速幂。