数据结构与算法-第七章 查找技术

查找的基本概念

关键码

关键码：可以标识一个记录（数据元素、结点、顶点）的某个数据项
键值：关键码的值
主关键码：可以唯一标识一个记录的关键码
次关键码：不能唯一标识一个记录的关键码

查找

• 查找：在相同类型的记录构成的集合中找出满足给定条件的记录
  给定的查找条件可能是多种多样的
  把查找条件限制为“匹配”，即查找关键码等于给定值的记录
• 查找表是由同一类型的数据元素（或记录）构成的集合。
• 查找的结果 ：若在查找集合中找到了与给定值相匹配的记录，则称查找成功，并给出整个记录的信息，或指示该记录在查找表中的位置；否则，称查找失败，查找结果给出**“空记录”或“空指针”**
• 对查找表常进行的操作：
  • 静态查找
    (1)查询某个“特定的”数据元素是否在查找表中
    (2)检索某个“特定的”数据元素的各种属性
  • 动态查找
    (3)在查找表中插入一个数据元素
    (4)从查找表中删去某个数据元素
• 静态查找 ：不涉及插入和删除操作的查找
  静态查找只注重查找效率，适用于：
  （1）查找集合一经生成，便只对其进行查找，而不进行插入和删除操作
  （2）经过一段时间的查找之后，集中地进行插入和删除等修改操作
• 动态查找 ：涉及插入和删除操作的查找
  动态查找要求插入、删除、查找均有较好的效率，适用于：查找与插入和删除操作在同一个阶段进行
  例如：当查找成功时，要删除查找到的记录
  当查找不成功时，要插入被查找的记录

查找结构

查找的方法取决于查找表的结构。

• 查找结构 ：面向查找操作的数据结构 ，即查找基于的数据结构
• 已经有了数据结构的概念，为什么要强调查找结构？
  （1）几乎所有的数据结构都提供了查找作为基本操作，但对于数据结构整体来说，查找并不是最重要的操作
  （2）对于查找结构来说，查找是最重要的基本操作，重要的是查找效率
  （3）数据结构 + 算法 = 程序：不同的查找结构，会获得不同的查找效率
  
• 查找基于的数据模型是集合
  集合：
  • 线性表：适用于静态查找，顺序查找、折半查找等技术
  • 树表：适用于动态查找，二叉排序树的查找技术
  • 散列表：静态查找和动态查找均适用，采用散列技术
• 注意到，都是把集合组织成XXX表，为什么？
  理解起来，集合最常用的表示法是列举法，习惯上，也称为表

查找算法的性能

平均查找长度

• 如何评价查找算法的效率呢？
  和关键码的比较次数

• 关键码的比较次数与哪些因素有关呢？
  平均查找长度(Average Search Length)：查找算法进行的关键码比较次数的数学期望值
  

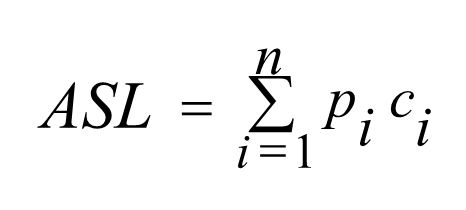
  • 其中：n：问题规模，查找集合中的记录个数
    p_i：查找第 i 个记录的概率
    c_i：查找第 i 个记录所需的关键码的比较次数
  • 如果 pi 是已知的，则平均查找长度只是问题规模的函数
    pi 与算法无关，取决于具体应用
    ci 取决于算法

• 对顺序表而言
  ASL = nP1+(n-1)P2+…+2Pn-1-+Pn

• 在等概率查找的情况下，顺序表查找成功的平均查找长度为：Pi=1/n; Ci=n-i+1
  

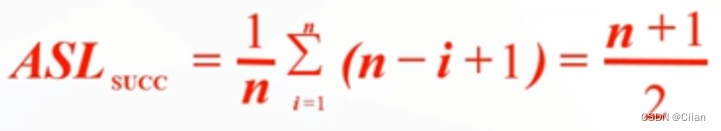
• 若查找概率无法事先测定，则查找过程采取的改进办法是，附设一个访问频度域或者在每次查找之后，将刚刚查找到的记录直接移至表尾的位置上。

顺序查找

顺序查找的基本思想

• 顺序查找（线性查找）：从线性表的一端向另一端逐个将记录与给定值进行比较，若相等，则查找成功，给出该记录在表中的位置；若整个表检测完仍未找到与给定值相等的记录，则查找失败，给出失败信息

int SeqSearch1(int r[ ], int n, int k)
{   
     int i = n;
     while (i > 0 && r[i] != k)
         i--;
     return i;
}

改进的顺序查找

• 顺序查找的改进：设置“哨兵”，就是待查值，放在查找方向的尽头处，免去了每一次比较后都要判断查找位置是否越界

//改进前
int LineSearch :: SeqSearch1(int k)
{   
     int i = n;
     while (i > 0 && data[i] != k)
         i--;
     return i;
}
//改进后
int LineSearch :: SeqSearch2(int k) 
{   
     int i = n; 
     data[0] = k; 
     while (data[i] != k)
        i--;
     return i;
}

顺序查找的时间性能

查找成功：
查找不成功：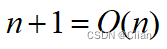

顺序查找的优缺点

• 顺序查找的缺点：查找效率较低
  特别是当待查找集合中元素较多时，不推荐使用顺序查找
• 顺序查找的优点：算法简单而且使用面广
  （1）对表中记录的存储没有任何要求，顺序存储和链接存储均可
  （2）对表中记录的有序性也没有要求，无论记录是否按关键码有序均可

折半查找

折半查找的基本思想

• 折半查找（对半查找、二分查找）：在有序表（假设为递增）中，取中间记录作为比较对象，若给定值与中间记录相等，则查找成功；若给定值小于中间记录，则在有序表的左半区继续查找；若给定值大于中间记录，则在有序表的右半区继续查找。不断重复上述过程，直到查找成功，或查找区域无记录，查找失败
  

折半查找的运行实例

折半查找的非递归算法

int LineSearch :: BinSearch1(int k)               /*查找集合存储在r[1]~r[n]*/
{
    int mid, low = 1, high = n;                   /*初始查找区间是[1, n]*/
    while (low <= high)                           /*当区间存在时*/
{ 
        mid = (low + high) / 2;            
        if (k < data[mid])  high = mid - 1;
        else  if (k > data[mid])  low = mid + 1; 
        else return mid;                         /*查找成功，返回元素序号*/
    }
    return 0;                                    /*查找失败，返回0*/
}

折半查找的递归算法

int LineSearch :: BinSearch2(int low, int high, int k) 
{   
    int mid;
    if (low > high) return 0;                                  /*递归的边界条件*/
    else {
        mid = (low + high) / 2;
        if (k < data[mid]) return BinSearch2(low, mid-1, k);
        else if (k > data[mid]) return BinSearch2(mid+1, high, k); 
        else return mid;                   /*查找成功，返回序号*/
    }
}

平均查找长度

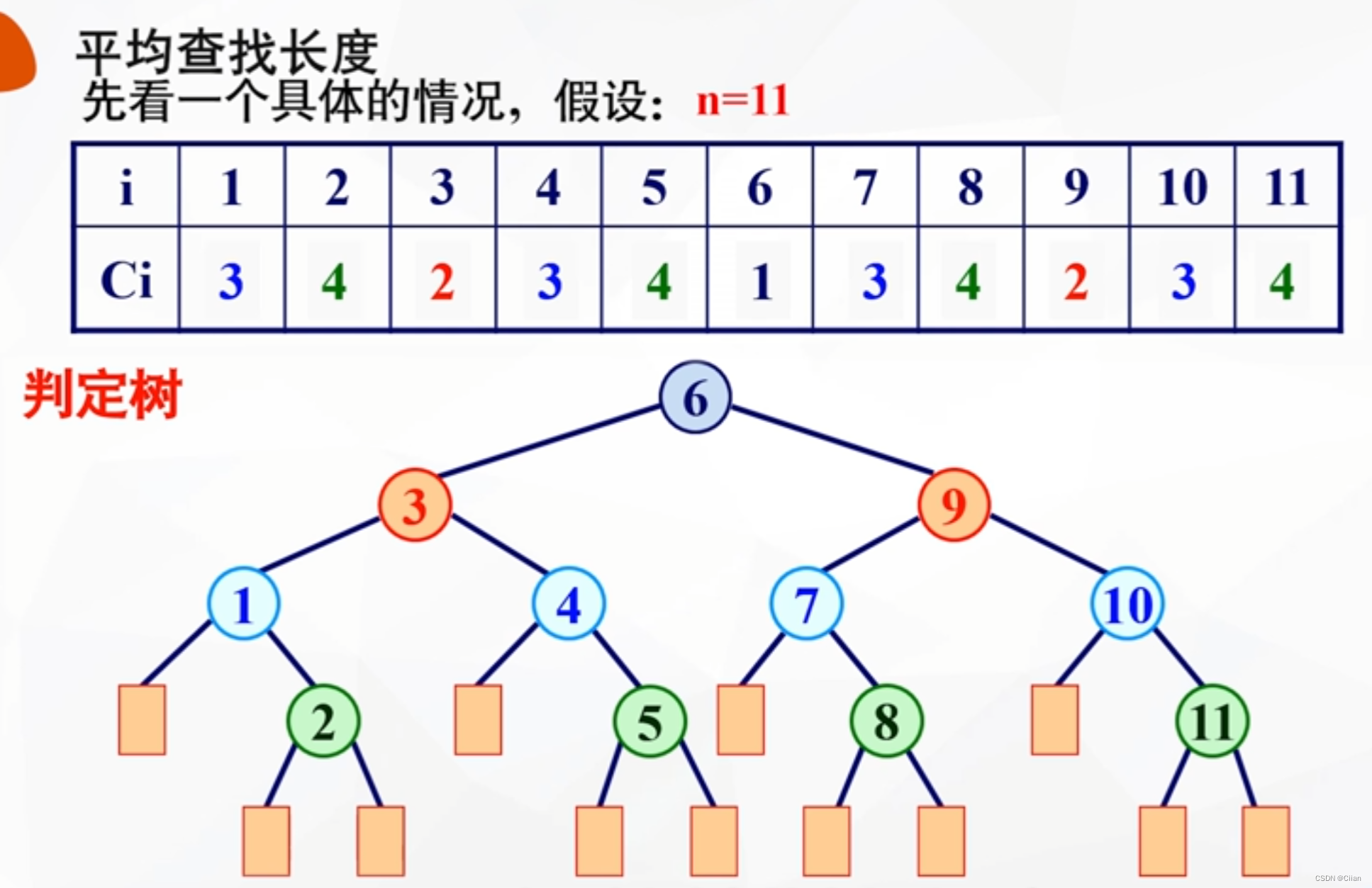
• 找到有序表中任一记录的过程就是走了一条从根结点到与该记录相应的结点的路径；
• 给定值进行比较的关键字个数恰是该结点在判定树上的层次数。

判定树

• 判定树（折半查找判定树）：描述折半查找判定过程的二叉树
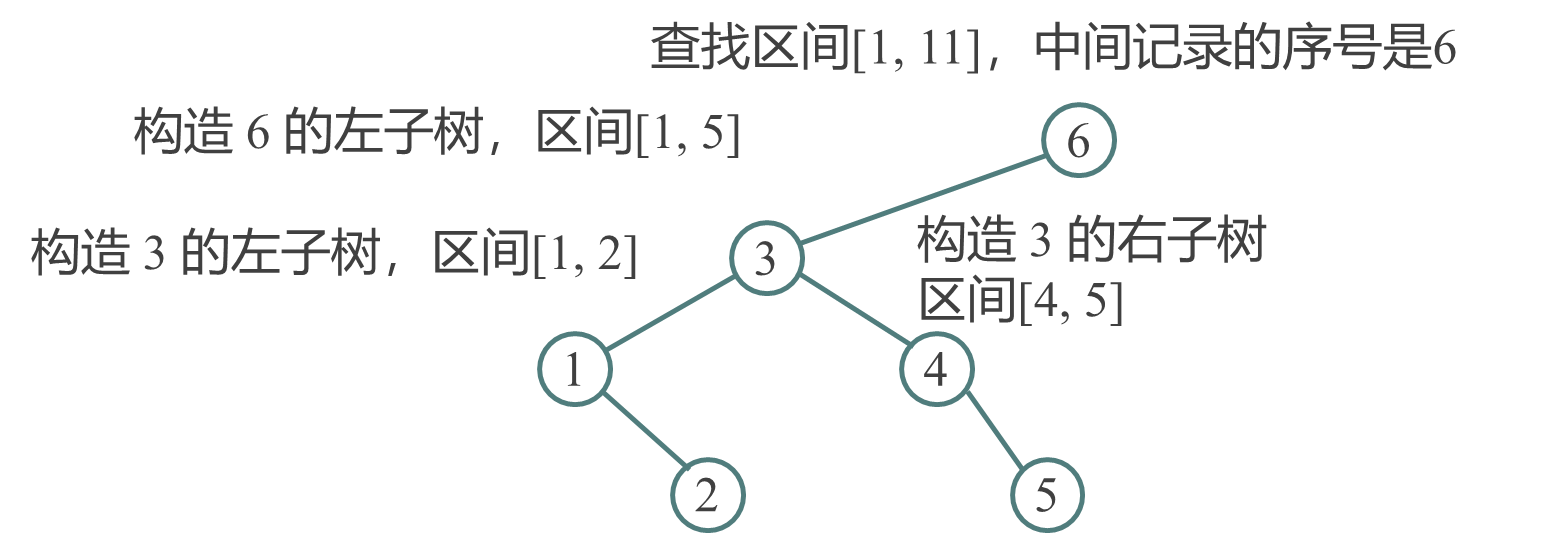
• 设查找区间是[low, high]，判定树的构造方法：
  （1）当low＞high时，判定树为空；
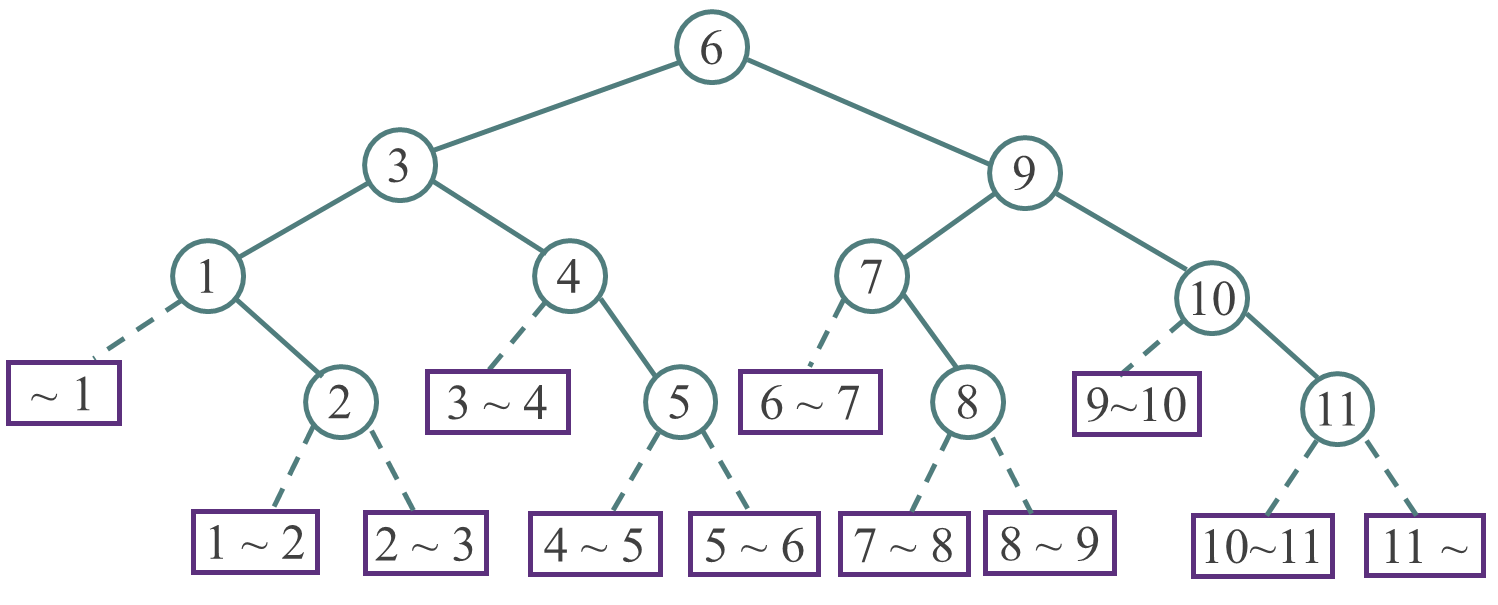
  （2）当low ≤ high时，判定树的根结点是有序表中序号为mid=(low+high)/2的记录，根结点的左子树是与有序表r[low]~r[mid-1]相对应的判定树，根结点的右子树是与有序表 r[mid+1] ~ r[high] 相对应的判定树。
• 例如，结点个数（查找集合的记录个数）为11的判定树
  

折半查找的性能分析

• 查找第 4 个元素比较多少次？
  折半查找任一记录的过程，即是判定树中从根结点到该记录结点的路径，和给定值的比较次数等于该记录结点在树中的层数
  
  
  假设n=2^h-1并且查找概率相等，则：在n>50时，可得近似结果≈log₂(n+1)-1
• 查找不成功的过程是从根结点到外部结点的路径，和给定值进行的比较次数等于该路径上内部结点的个数。
  查找成功的平均比较次数 = (1×1+2×2+3×4+4×4)/11 = 3
  查找不成功的平均比较次数 = (3×4+4×8)/12 = 11/3
  注意：当计算查找失败的平均长度时，层数需要依次减1，即原先第四层变为第三层，然后进行查找失败的次数的计算，
  
• 折半查找只适用于有序表，且限于顺序存储结构。

二叉排序树(动态查找)

树表的提出

• 如何在一个大型的数据集合上进行动态查找？
  • 顺序查找：不要求元素的有序性，插入、删除的性能是O(1)，查找性能是O(n)
  • 折半查找：查找性能是O(log2n)，为保证元素的有序性，插入、删除要移动元素，性能是O(n)
• 有没有一种查找结构，使得插入、删除、查找均具有较好效率？
  树表：将查找集合组织成树的结构 =》二叉排序树

二叉排序树的定义

• 二叉排序树（二叉查找树）：或者是一棵空的二叉树，或者是具有下列性质的二叉树：
  （1）若它的左子树不空，则左子树上所有结点的值均小于根结点的值
  （2）若它的右子树不空，则右子树上所有结点的值均大于根结点的值
  （3）它的左右子树也都是二叉排序树
• 二叉排序树的定义是一个递归定义的过程
  二叉排序树是记录之间满足某种大小关系的二叉树
• 二叉排序树不但拥有类似于折半查找的特性，又采用了链表作存储结构，因此是动态查找表的一种适宜表示。

二叉排序树的存储

二叉链表

二叉排序树的类定义

class BiSortTree                              
{
public:
     BiSortTree(int a[ ], int n);       
     ~ BiSortTree( ) {Release(root);} 
     BiNode<int> *InsertBST(int x) {return InsertBST(root, x);}
     void DeleteBST(BiNode<int> *p, BiNode<int> *f );      
     BiNode<int> *SearchBST(int k) {return SearchBST(root, k);}
private:
     BiNode<int> *InsertBST(BiNode<int> *bt , int x);             
     BiNode<int> *SearchBST(BiNode<int> *bt, int k);    
     void Release(BiNode<DataType> *bt);     
     BiNode<int> *root;                              
};

二叉排序树的实现——查找

在二叉排序树中查找给定值 k 的过程是
（1）若 bt 是空树，则查找失败；
（2）若k＝bt->data，则查找成功；
（3）若k＜bt->data，则在 bt 的左子树上查找；
（4）若k > bt->data，在 bt 的右子树上查找。
二叉排序树的查找效率在于只需查找二个子树之一

BiNode<int> * BiSortTree :: SearchBST(BiNode<int> *bt, int k)
{
      if (bt == nullptr) return nullptr;
      if (bt->data == k) return bt;
      else if (bt->data > k) return SearchBST(bt->lchild, k);
      else return SearchBST(bt->rchild, k);
}

• 在二叉排序树上进行查找，类似折半查找
  用链式存储
• 整个查找过程生成了一条查找路径：
  查找成功：从根结点出发，沿着左分支或右分支逐层向下直至关键字等于给定值的结点：
  查找不成功：从根结点出发，沿着左分支或右分支逐层向下直至指针指向空树为止。

二叉排序树的实现——插入

• " 插入"操作在查找不成功时才进行
• 若二叉排序树为空树，则新插入的结点为新的根结点；
  否则，新插入的结点必为一个新的叶子结点，其插入位置由查找过程得到。

BiNode<int> * BiSortTree::InsertBST(BiNode<int> *bt, int x)
{
     if (bt == nullptr) {                
          BiNode<int> *s = new BiNode<int>; s->data = x;
          s->lchild = s->rchild = nullptr;
          bt = s;
          return bt;
     }
     else if (bt->data > x) bt->lchild = InsertBST(bt->lchild, x);
     else bt->rchild = InsertBST(bt->rchild, x);
}

二叉排序树的实现——构造

• 通过升序序列可以构建有序的二叉排序树
  一个无序序列可以通过构造一棵二叉排序树而得到一个有序序列（中序序列）。
  中序遍历二叉排序树可得到关键字有序序列。
• （1）每次插入的新结点都是二叉排序树上新的叶子结点;
  （2）找到插入位置后，不必移动其它结点，仅需修改某个结点的指针；
  （3）在左子树/右子树的查找过程与在整棵树上查找过程相同；
  （4）新插入的结点没有破坏原有结点之间的关系。

BiSortTree::BiSortTree(int a[ ], int n)
{
     root = nullptr;
     for (int i = 0; i < n; i++)
          root = InsertBST(root, a[i]);
}

void CreateBST(BSTree *bst){
	KeyType key;
	*bst=NULL;
	scanf ("%d",&key);
	while(key！=ENDKEY)
	{
		InsertBST(bst,Key);
		scanf("%d",&key)
	}
}

二叉排序树的实现——删除

• 如何在二叉排序树中删除一个元素？
  （1）从二叉排序树中删除一个结点之后，要仍然保持二叉排序树的特性；
  （2）当删除分支结点时破坏了二叉排序树中原有结点之间的链接关系，需要重新修改指针，使得删除结点后仍为一棵二叉排序树。
• 不失一般性，设待删除结点为p，其双亲结点为f，且 p 是 f 的左孩子，
  • 情况 1——被删除的结点是叶子结点
    操作：将双亲结点中相应指针域的值改为空。
    f->lchild = nullptr;
  • 情况 2——被删除的结点只有左子树或者只有右子树
    操作：将双亲结点中相应指针域指向被删除结点的左子树（或右子树）
    f->lchild = p->rchild;
  • 情况 3——被删除的结点既有左子树也有右子树
    操作：以其左子树中的最大值结点替换之，然后再删除该结点

    BiNode *par = p, *s = p->lchild;  
    while (s->rchild != nullptr)
    {
        par = s;
        s = s->rchild;
    }
    p->data = s->data;
    par->rchild = s->lchild; 
    

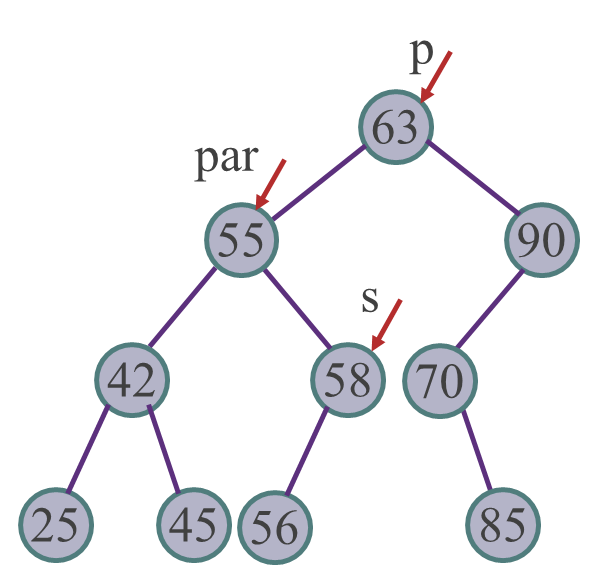
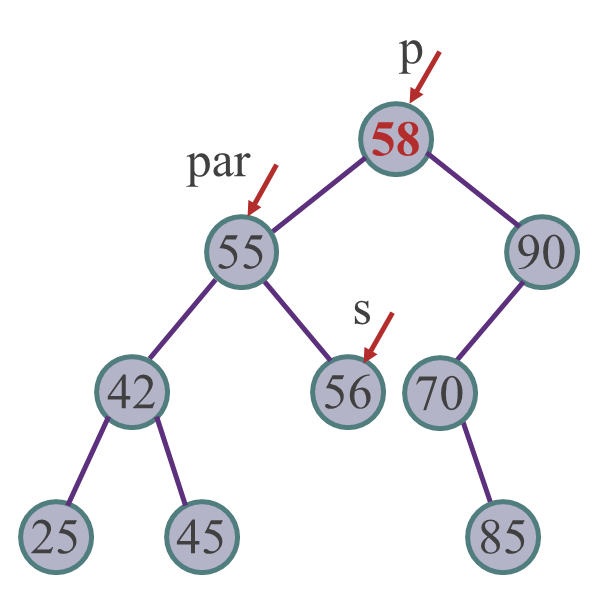
特殊情况：左子树中的最大值结点是被删结点的孩子
if (p == par) par->lchild = s->lchild;

template <typename DataTypa>
void BiSortTree::DeleteBST(BiNode<int> *p, BiNode<int> *f ) 
{
     if ((p->lchild == nullptr) && (p->rchild == nullptr)) {     //p为叶子
          f->lchild = NULL; delete p; return;
     }
     
     if (p->rchild == nullptr) {                 //p只有左子树
          f->lchild = p->lchild; delete p; return;
     }
     
     if (p->lchild == nullptr) {                 //p只有右子树
          f->lchild = p->rchild; delete p; return;
     }
     
     BiNode<int> *par = p, *s = p->lchild;              /*p的左右子树均不空*/
     while (s->rchild != nullptr)                      /*查找左子树的最右下结点*/
    {
        par = s;
        s = s->rchild;
    }
    p->data = s->data;
    if (par == p) par->rchild = s->lchild;  
    else par->lchild = s->lchild;             
    delete s;  
    
        /*查找右子树的最左下结点*/
    BiNode<int> *par = p, *s = p->rchild;    
    while (s->lchild != nullptr) 
    {
        par = s;
        s = s->lchild;
    }
    p->data = s->data;
    if (par == p) par->lchild = s->rchild;    
    else par->rchild = s->rchild;  
    delete s;           

二叉排序树的性能分析

• 1、中序遍历二叉排序树可以得到关键字的有序序列。
  2、在构造二叉排序树的时候，不需要移动其他结点。
  3、二叉排序树可以得到折半查找一样好的时间性能并且由于它是链式存储，所以二叉排序树的插入和删除相对的元素移动量都是非常少的。
• 比较次数不超过树的深度
• 插入、删除、查找的时间复杂度相同
  在二叉排序树中执行插入和删除操作-> 查找插入和删除的位置->修改相应指针
• 二叉排序树的深度
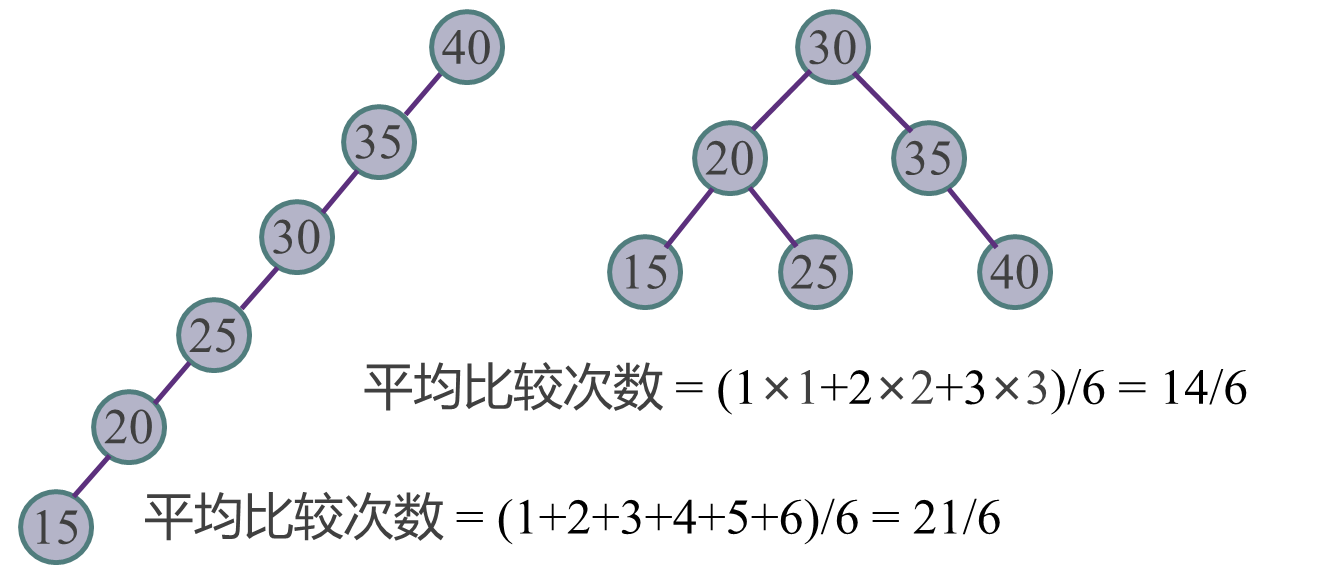
  最坏情况：退化为线性查找
  最好情况：相当于折半查找
  平均情况：O(n) ~ O(log₂n)
  

平衡二叉树

平衡二叉树的提出

二叉排序树的深度取决于给定查找集合的排列，即结点的插入顺序

• 具有 n 个结点的二叉排序树，最小深度是多少？有什么特征？
  • 完全二叉树的深度：
    
  • 左右子树的深度相同
• 平衡二叉树
  • 深度
    
  • 左右子树的深度相差 1

平衡二叉树（AVL树）的定义

AVL（由 Adelson-Velsky 和 Landis 共同发明）

• 平衡因子：该结点的左子树的深度减去右子树的深度
• 平衡二叉树：或者是一棵空的二叉排序树，或者是具有下列性质的二叉排序树：
  （1）根结点的左子树和右子树的深度最多相差 1;
  （2）根结点的左子树和右子树也都是平衡二叉树
  在平衡二叉树中， 结点的平衡因子是1、0 或 -1
• 最小不平衡子树
  最小不平衡子树：以距离插入结点最近的、且平衡因子的绝对值大于 1 的结点为根的子树
  
  且入且判断，一旦失衡立即调整
  只调整最小不平衡子树，并且不影响其他结点
• 如何调整最小不平衡子树呢？

算法：平衡调整
输入：平衡二叉树，新插入结点A
输出：新的平衡二叉树
         1.  找到最小不平衡子树的根结点 D
         2.  根据结点A和结点D之间的关系，判断调整类型
         3.  根据类型、遵循**扁担原理**和**旋转优先**原则进行相应调整
            （1）**LL型、RR型：调整一次**
            （2）**LR型、RL型：调整两次**

LL 顺时针
RR 逆时针
LR 先逆后顺
RL先顺后逆

平衡二叉树的平衡调整——LL型、RR型

• 例 1：设序列{40, 35, 20}，构造平衡二叉树
  
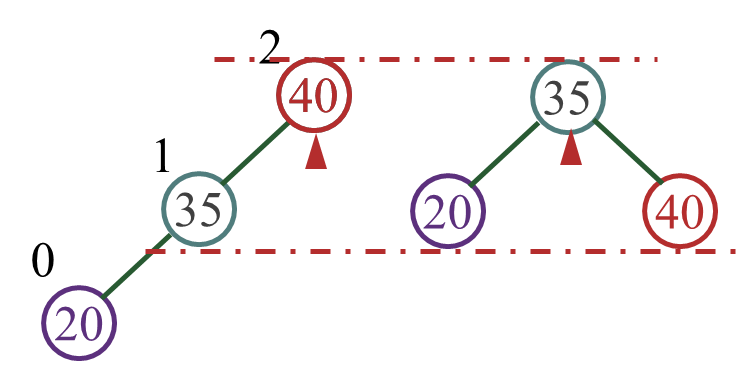
  新插入结点20和最小不平衡子树根结点40之间的关系——LL型，顺时针旋转
  扁担原理：将根结点看成是扁担中肩膀的位置

• 例 2：设序列{40, 35, 20,15, 25, 10}，构造平衡二叉树
  
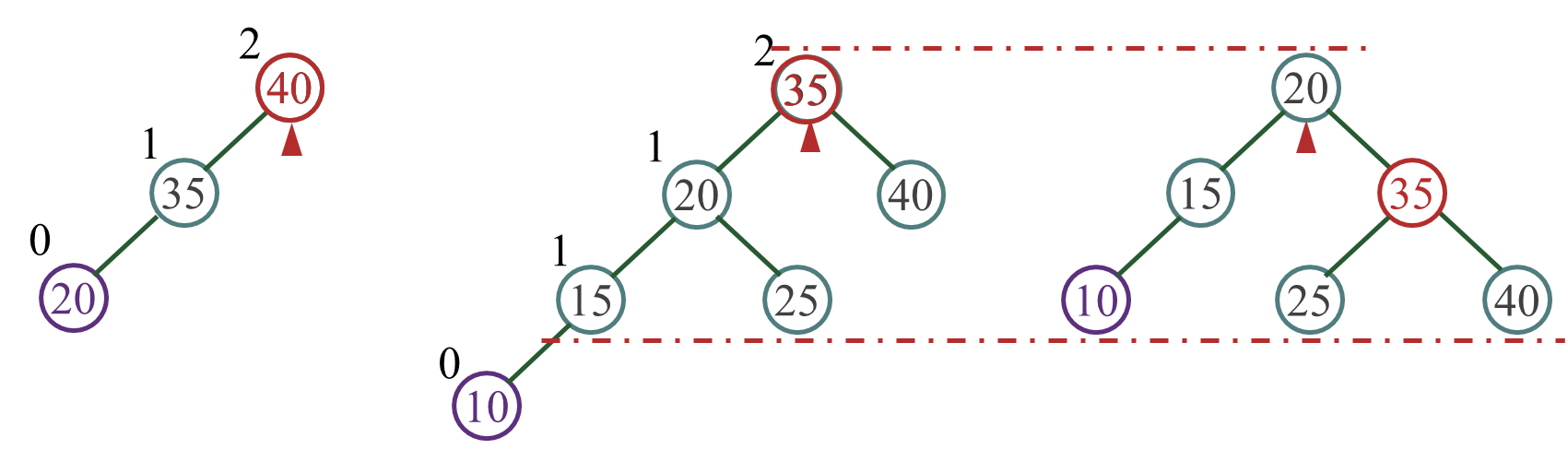
  新插入结点10和最小不平衡子树根结点35之间的关系——LL型
  扁担原理：将根结点看成是扁担中肩膀的位置
  旋转优先：旋转下来的结点作为新根结点的孩子

• 例 3：设序列{20, 35, 40}，构造平衡二叉树
  

新插入结点40和最小不平衡子树根结点20之间的关系——RR型，逆时针
扁担原理：将根结点看成是扁担中肩膀的位置

• 例 4：设序列{20, 35, 40, 38, 45, 50}，构造平衡二叉树
  
  新插入结点50和最小不平衡子树根结点35之间的关系——RR型
  扁担原理：将根结点看成是扁担中肩膀的位置
  旋转优先：旋转下来的结点作为新根结点的孩子

平衡二叉树的平衡调整——LR型、RL型

• 例 1：设序列{35, 40, 20, 15, 30, 25}，构造平衡二叉树

新插入结点25和最小不平衡子树根结点35之间的关系——LR型，先逆后顺

• 例 2：设序列{35, 20, 30}，构造平衡二叉树
  
  新插入结点30和最小不平衡子树根结点35之间的关系——LR型
• 例 3：设序列{35, 45, 20, 50, 40, 38} ，构造平衡二叉树
  
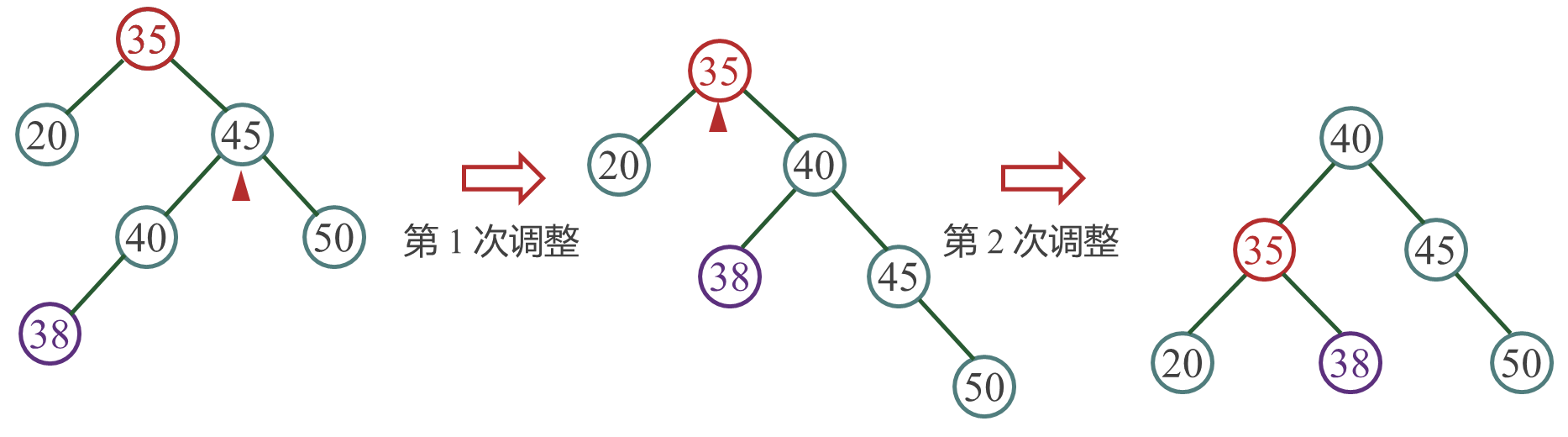
  新插入结点38和最小不平衡子树根结点35之间的关系——RL型，先顺后逆

哈希(动态查找)

B树

B树的定义及特征

B树：一棵m阶的B树 或者为空树，或者为满足下列特性的m叉树：
（1）每个结点至多有 m 棵子树；
（2）根结点至少有两棵子树；
（3）除根结点和叶子结点外，所有结点至少有? m/2 ?棵子树；

（4）所有结点都包含以下数据：
（n，A0，K1，A1，K2，…，Kn，An）
其中，n（?m/2? - 1≤n≤m -1）为关键码的个数，Ki（1≤i≤n）为关键码，且Ki ＜ Ki +1（1≤i≤n-1），Ai（0≤i≤n）为指向子树根结点的指针，且指针Ai 所指子树中所有结点的关键码均小于K _i+1 大于K_i 。

（5）叶子结点都在同一层；

B树的插入

假定在 m 阶 B 树中插入关键码key，设n=m-1，插入过程如下：
（1）定位：确定关键码key应该插入哪个终端结点并返回该结点的指针p。
若 p 中的关键码个数小于n，则直接插入关键码key；
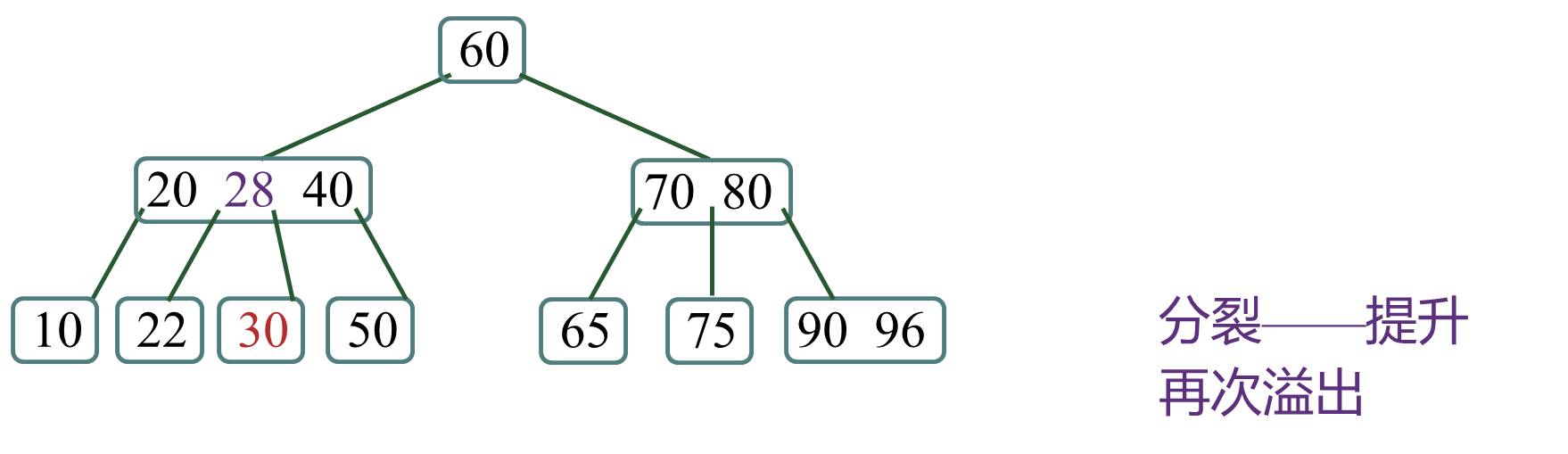
否则，结点 p 的关键码个数溢出，执行“分裂——提升”过程。


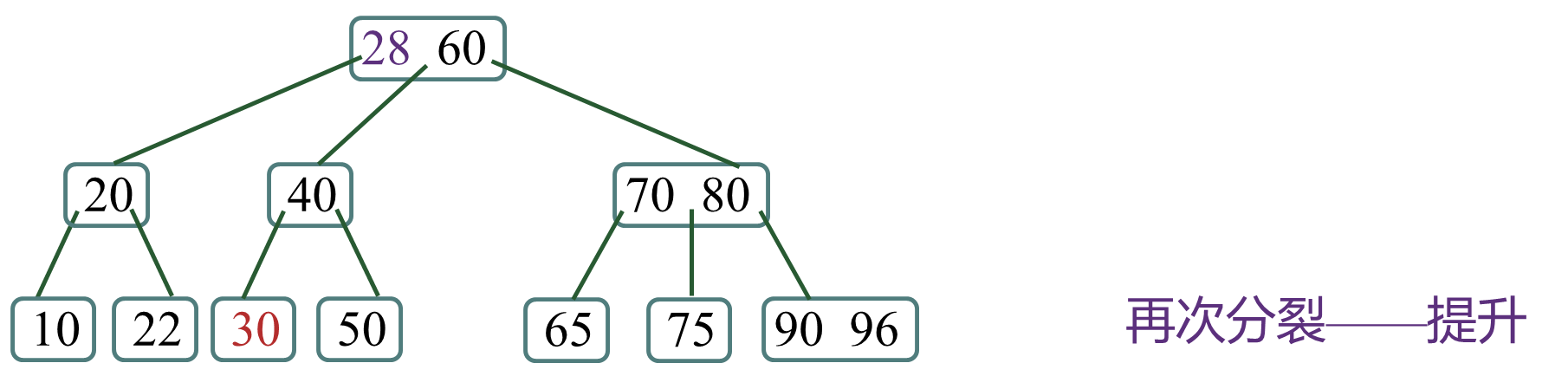
（2）分裂——提升：将结点 p“分裂”成两个结点，分别是p₁和p₂，把中间的关键码k“提升”到父结点，并且k的左指针指向p₁，右指针指向p₂。

如果父结点的关键码个数也溢出，则继续执行“分裂——提升”过程。显然，这种分裂可能一直上传，如果根结点也分裂了，则树的高度增加了一层。

B树的删除

• 如何删除二叉排序中的一个结点？
  情况 1——被删除的结点是叶子结点
  情况 3——被删除的结点既有左子树也有右子树

B树的删除

• （1）定位：确定关键码key在哪个结点并返回该结点的指针q。
  假定key是结点 q 中的第 i 个关键码Ki，有以下两种情况：
  1.1 若结点 q 是叶子结点，则删除key；
  1.2 若结点 q 不是叶子结点，则用 Ai(指向key的指针) 所指子树中的最小值 x 替换Ki；删除 x；
• （2）判断是否下溢
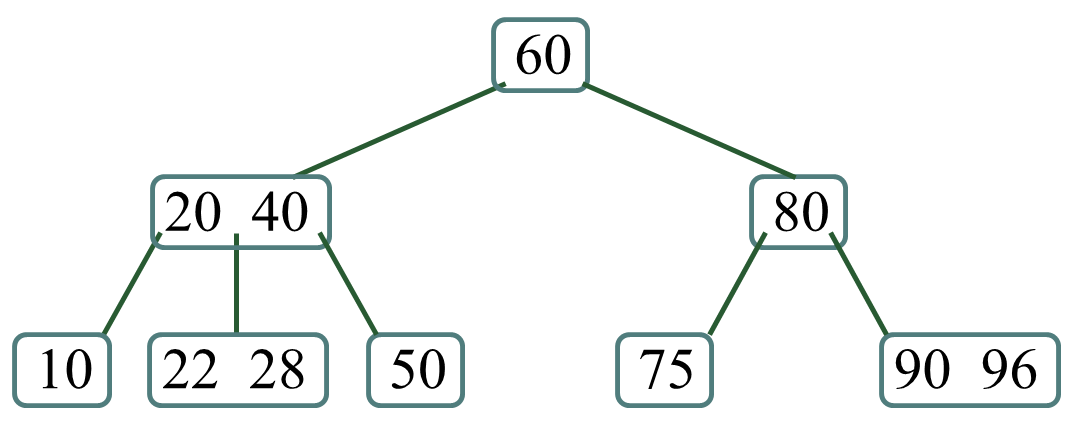
  • 2.1 如果叶子结点中关键码的个数大于 -1，则直接删除；
    
    
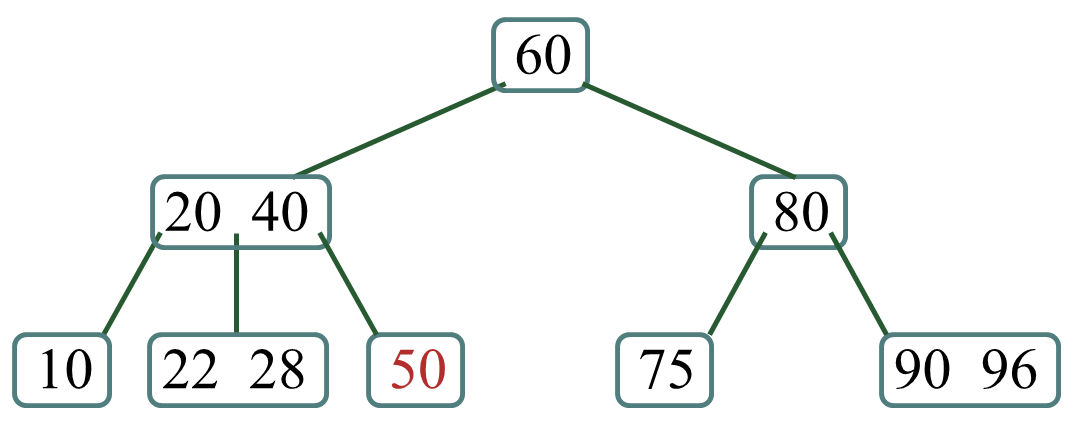
  • 2.2 否则，删除操作涉及到兄弟结点

    • 2.2.1 兄弟结点的关键码个数大于 ，则向兄弟结点借一个关键码，并且借来的关键码“上移”到双亲结点，双亲结点相应关键码“下移”；
      
      

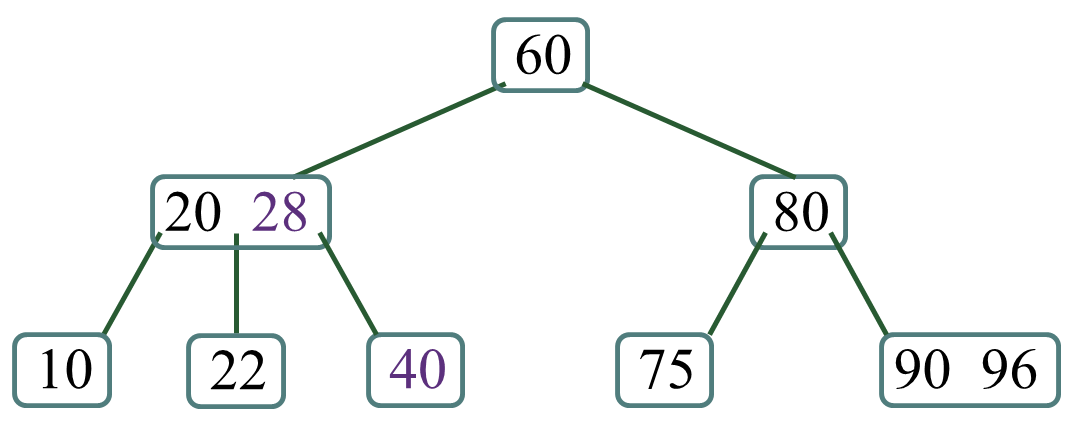
    • 2.2.2 兄弟结点的关键码个数不大于 ，则执行“合并”兄弟操作；
      删除空结点，并将双亲结点中的相应关键码“下移”到合并结点中；
      
      
      如果双亲结点的关键码个数发生下溢，则双亲结点也要进行借关键码或合并操作
      

B树的查找及查找性能

散列查找（哈希查找）

• 查找操作要完成什么任务？
  通过待查值k确定 k 在存储结构中的位置
• 前面学过哪些查找技术？这些查找技术有什么共性呢？
  （1）顺序查找 == 、!= O(n)
  （2）折半查找 <、==、> O(log2n)
  （3）二叉排序树查找 O(n) ~ (log2n)
  通过一系列的给定值与关键码的比较，查找效率依赖于查找过程中进行的给定值与关键码的比较次数
• 能否不用比较，通过关键码能够直接确定存储位置？
  在存储位置和关键码之间建立一个确定的对应关系
  设关键码key在存储结构中的位置是addr，则有addr = H(key)。
• 查找技术
  比较式查找
  计算式查找

散列的基本思想

散列的基本思想：在记录的关键码和存储地址之间建立一个确定的对应关系，通过计算得到待查记录的地址。
哈希函数是一个映象，即：将关键字的集合映射到某个地址集合上。

散列的基本概念

散列表：采用散列技术存储查找集合的连续存储空间
散列函数：将关键码映射为散例表中适当存储位置的函数。
散列地址：由散列函数所得的存储地址。

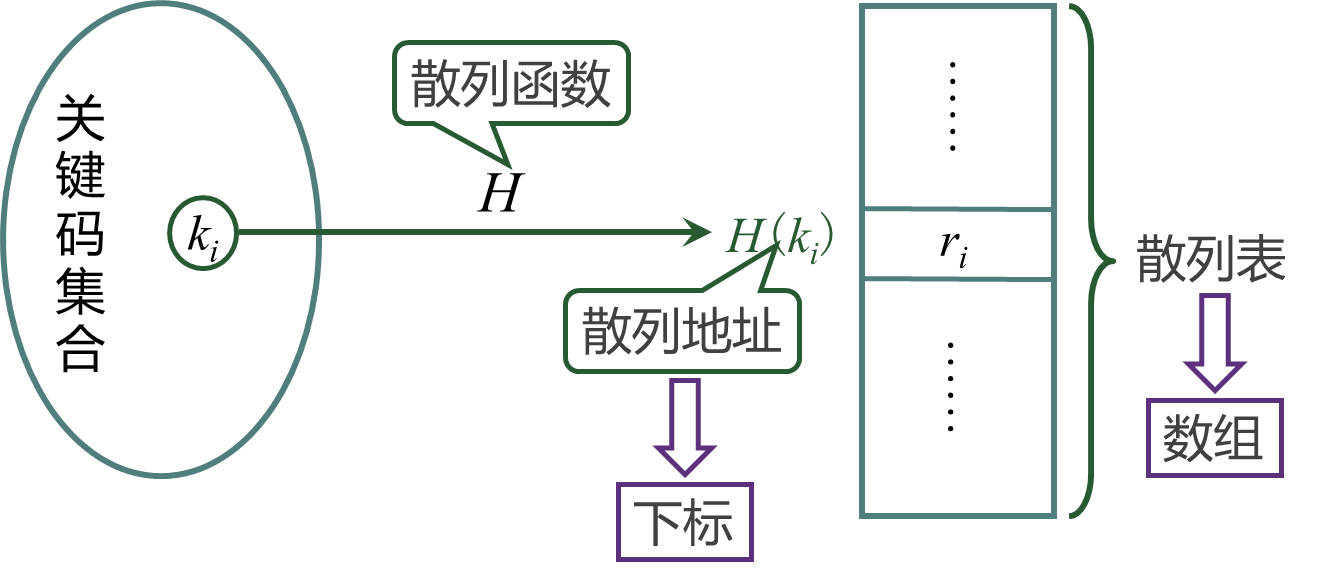
散列技术的关键问题

• 如何设计散列函数？如何解决冲突？
  冲突：对于两个不同关键码k_i≠k_j，有H(k_i)＝H(k_j)。
  同义词：k_i和 k_j 相对于H 称做同义词。
• 散列是一种完整的存储结构吗？
  散列只是通过记录的关键码定位该记录，没有完整地表达记录之间的逻辑关系，所以，散列主要是面向查找的存储结构
• 散列技术一般不适用于多个记录有相同关键码的情况，也不适用于范围查找
  散列技术最适合回答的问题是：如果有存在的话，找出哪个记录的关键码等于待查值

哈希表

根据设定的哈希函数H（key)和所选中的处理冲突的方法，将一组关键字映象到一个有限的、地址连续的地址集（区间）上，并以关键字在地址集中的“象”作为相应记录在表中的存储位置，如此构造所得的查找表称之为“哈希表”。

散列函数（哈希函数）

在一般情况下，需在关键字与记录在表中的存储位置之间建立一个函数关系，以f(key)作为关键字为key的记录在表中的位置，通常称这个函数f(key)为哈希函数。

散列函数的设计原则

很难找到一个不产生冲突的哈希函数。一般情况下，只能选择恰当的哈希函数，使冲突尽可能少地产生。
如何设计散列函数？
（1）计算简单。散列函数不应该有很大的计算量，否则会降低查找效率。
（2）地址均匀。函数值要尽量均匀散布在地址空间，保证存储空间的有效利用并减少冲突。
若是非数字关键字，则需先对其进行数字化处理。

几种常见的散列函数

• 直接定址法
  散列函数是关键码的线性函数，即：
  H(key) = a * key + b （a，b为常数）
  例 1：关键码集合为{10, 30, 50, 70, 80, 90}，选取的散列函数为H(key)=key/10，散列表构造过程如下：
  
  适用于：事先知道关键码，关键码集合不是很大且连续性较好
  
  关键字第一个字母/2再对应到此地址的内容。

• 数字分析法
  假设关键字集合中的每个关键字都是由S位数字组成(u₁,u₂,…,u_s),分析关键字集中的全体，并从中提取分布均匀的若干位或它们的组合作为地址。
  

• 平方取中法
  对关键码平方后，按散列表大小，取中间的若干位作为散列地址。
  例 3：散列地址为 2 位，设计平方取中法的散列函数。
  
  
  不同关键字会以较高的概率产生不同的哈希地址
  适用于：事先不知道关键码的分布且关键码的位数不是很大

• 折叠法
  ◆将关键字分割成若干部分，然后取它们的叠加和为哈希地址。
  例：当图书馆馆藏不到1000时，有图书编号为12360324711202065，那它对应的哈希地址应该为多少？
  

• 除留余数法
  H(key)=key MOD p
  表长是m,p是<=m的最大素数
  p小于等于表长（最好接近表长）的最大素数或不包含小于20质因子的合数
  
  适用于：最简单、最常用，不要求事先知道关键码的分布

处理冲突的方法

开放定址法

开放定址法的基本思想

• 对于给定的关键码key执行下述操作：
  （1）计算散列地址：j = H(key)
  （2）如果地址 j 的存储单元没有存储记录，则存储key对应的记录；
  （3）如果在地址 j 发生冲突，则寻找一个空的散列地址，存储key对应的记录；
  闭散列表：用开放定址法处理冲突得到的散列表
• 如何寻找一个空的散列地址呢？
  （1）线性探测法；（2）二次探测法；（3）随机探测法……

闭散列表的类定义

const int MaxSize = 100;
class HashTable1
{
public:
     HashTable1( );  
     ~HashTable1( );
     int Insert(int k);     
     int Delete(int k);    
     int Search(int k);    
private:
     int H( );                  
     int ht[MaxSize];     
};
HashTable1 :: HashTable1( )
{
     for (int i = 0; i < MaxSize; i++)
          ht[i] = 0;           
}
HashTable1 :: ~HashTable1( )
{
}

线性探测法

线性探测法：从冲突位置的下一个位置起，依次寻找空的散列地址。
设散列表的长度为m，对于键值key，发生冲突时，寻找空散列地址的公式为：
H_i=(H(key)＋d_i) % m （d_i=1，2，…，m-1）
例 1：设关键码集合为 {47, 7, 29, 11, 16, 92, 22, 8, 3}，散列表表长为11，散列函数为H(key)=key mod 11，用线性探测法处理冲突，散列表的构造过程如下：

堆积：非同义词对同一个散列地址争夺的现象

算法：Search
输入：闭散列表ht[ ]，待查值k
输出：如果查找成功，则返回记录的存储位置，否则返回查找失败的标志-1
      1. 计算散列地址 j；
      2. 探测下标i初始化：i = j；
      3. 执行下述操作，直到 ht[i] 为空：
           3.1 若 ht[i] 等于 k，则查找成功，返回记录在散列表中的下标；
           3.2 否则，i 指向下一单元；
      4. 查找失败，返回失败标志-1；

int HashTable1 :: Search(int k) 
{
     int i, j = H(k);                               //计算散列地址
     i = j;                                              //设置比较的起始位置
     while (ht[i] != 0)
     {
          if (ht[i] == k) return i;              //查找成功
          else i = (i + 1) % m;                 //向后探测一个位置
     }
     return -1;                                       //查找失败
}

二次探测法

• 二次探测法：以冲突位置为中心，跳跃式寻找空的散列地址。
• 设散列表的长度为m，对于键值key，发生冲突时，寻找空散列地址的公式为：
  H_i=(H(key)＋d_i) % m （d_i = 1²,-1²,2²,-2²,… , q²,-q²(q≤m/2)）
• 例 2：设关键码集合为 {47, 7, 29, 11, 16, 92, 22, 8, 3}，散列表表长为11，散列函数为H(key)=key mod 11，用二次探测法处理冲突，散列表的构造过程如下：
  
  

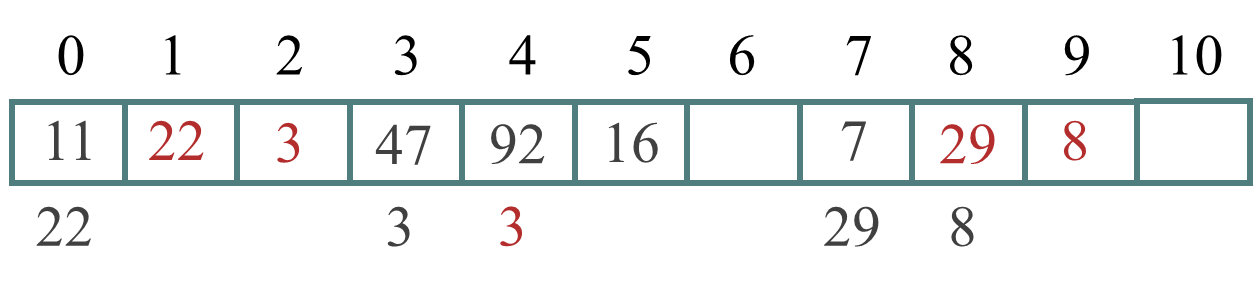
相对于线性探测法，二次探测法能够在一定程度上减少堆积

• 探测法处理冲突得到的闭散列表中，关键码11和22的散列地址相同，当删除11并把被删除单元清空时，同时也截断了与关键码11冲突的探测序列，再查找22就找不到了，所以删除不能简单地把被删除单元清空。解决方法是采用懒惰删除(lazy deletion),在被删除记录的位置上放一个特殊标记，标志一个记录曾经占用这个单元，但是现在已经不再占用了。如果沿着一个搜索序列查找时遇到一个标记，则查找过程应该继续进行下去。当在插入时遇到一个标记，那个单元就可以用于存储新记录。然而，为了避免插入相同的关键码，查找过程仍然要沿着探测序列查我下去。

拉链法

拉链法如何处理冲突？
对于给定的关键码key执行下述操作：
（1）计算散列地址：j = H(key)
（2）将key对应的记录插入到同义词子表 j 中；
同义词子表：所有散列地址相同的记录构成的单链表。
开散列表：用拉链法处理冲突得到的散列表。
开散列表中存储同义词子表的头指针，开散列表不会出现堆积现象

开散列表的类定义

const int MaxSize = 100;
class HashTable2
{
public:
     HashTable2( );  
     ~HashTable2( );
     int Insert(int k); 
     int Delete(int k);
     Node<int> * Search(int k);
private:
     int H( );                   
     Node<int> * ht[MaxSize];
};
HashTable2 :: HashTable2( )
{
      for (int i = 0; i < MaxSize; i++)
      {
           ht[i] = nullptr;
      } 
}

析构函数

HashTable2 :: ~HashTable2( )
{
      Node<int> *p = nullptr, *q = nullptr;
      for (int i = 0; i < MaxSize; i++)
      {
            p = q = ht[i];
            while (p != nullptr)
            {
                  p = p->next;
                  delete q;
                  q = p;
             }
      }
}

构造过程

例 1：设关键码集合为 {47, 7, 29, 11, 16, 92, 22, 8, 3}，散列表表长为11，散列函数为H(key)=key mod 11，用拉链法处理冲突，散列表的构造过程如下：

j = H(k);     
Node<int> *p = ht[j];
while (p != nullptr)
{
      if (p->data == k) break;
      else p = p->next;
}
if (p == null) {
     q = new Node<int>;   q->data = k;         
     q->next = ht[j]; ht[j] = q;
}

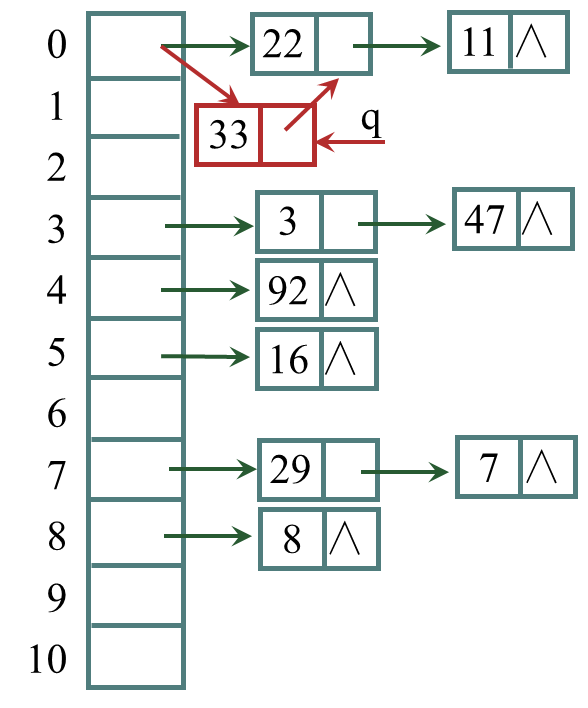
查找算法

Node<int> * HashTable2 :: Search(int k)
{
     int j = H(k);     
     Node<int> *p = ht[j];
     while (p != nullptr)
    {
          if (p->data == k) return p;
          else p = p->next;
     }
     return nullptr;            
}

散列查找的性能分析

• 散列技术的查找性能取决于什么？
  产生冲突后，仍然是给定值与关键码进行比较
• 影响冲突产生的因素有什么？
  （1）散列函数是否均匀
  （2）处理冲突的方法
• 例 1：设关键码集合为 {47, 7, 29, 11, 16, 92, 22, 8, 3}，散列表表长为11，散列函数为H(key)=key mod 11，用线性探测法和拉链法处理冲突，分析查找性能。
  
  
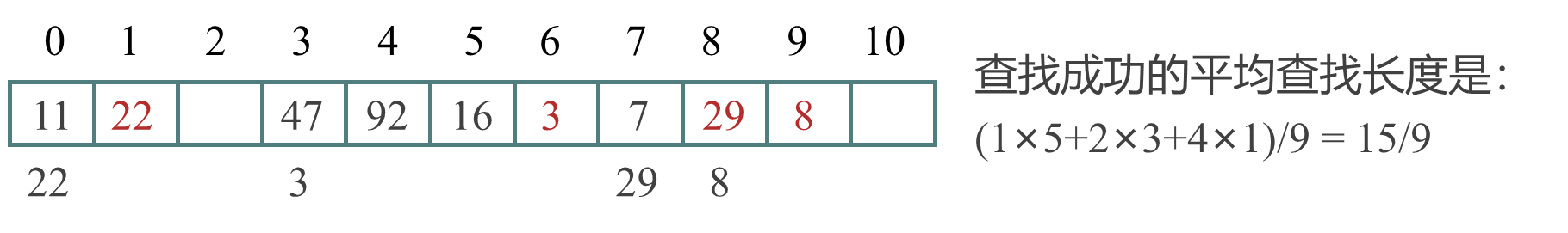
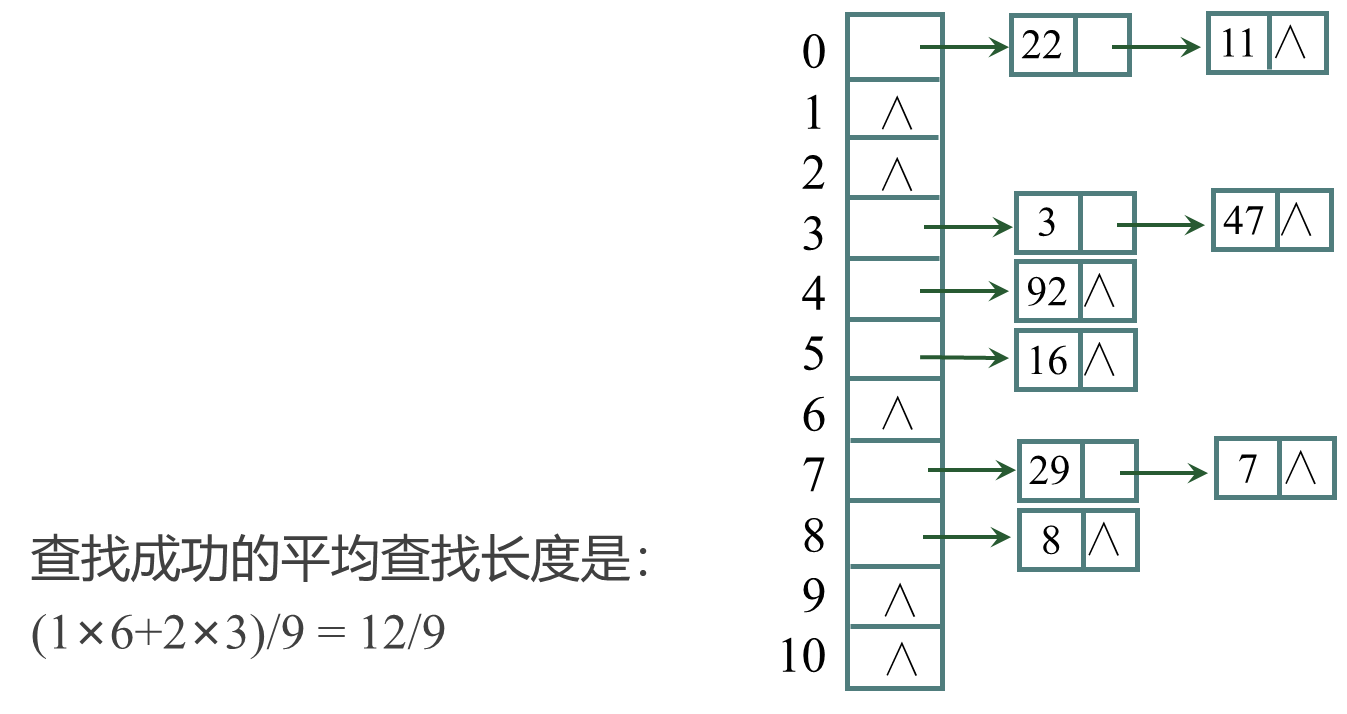
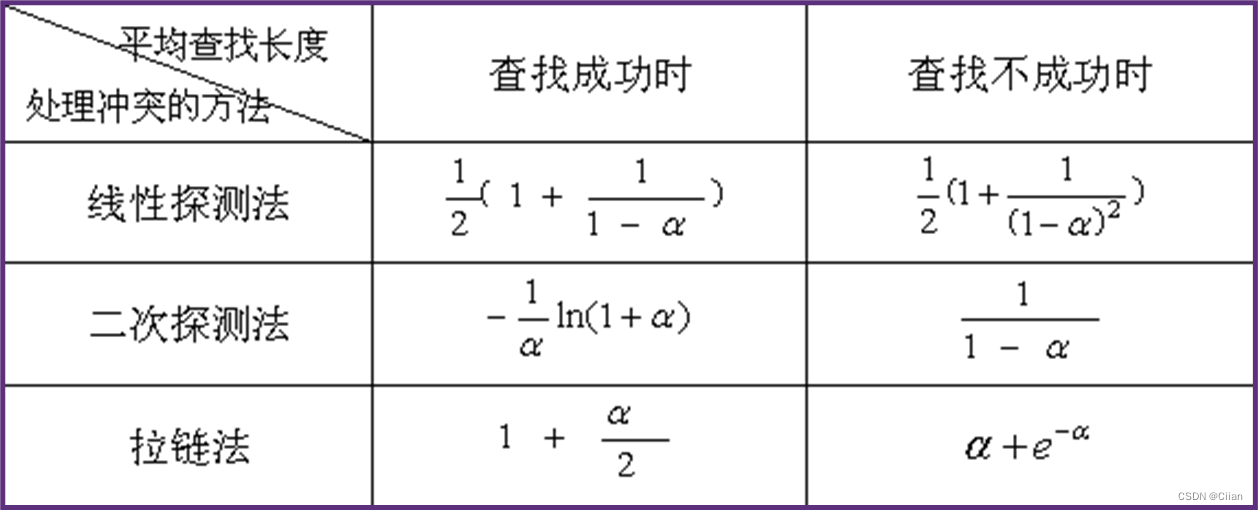
  （3）散列表的装填因子α
  
  散列表的平均查找长度是装填因子 α 的函数， 而不是查找集合中记录个数 n 的函数——O(1)！
  

闭散列表和开散列表的比较

闭散列表和开散列表的空间比较

闭散列表：
受数组空间限制，需要考虑存储容量
存储效率较高
开散列表：
没有记录个数的限制，但子表过长会降低查找效率
指针的结构性开销

闭散列表和开散列表的时间比较

• 闭散列表：
  有堆积现象，降低查找效率
  仅适用于静态查找
• 开散列表：
  不会产生堆积现象，效率较高
  适用于静态查找和动态查找

删除操作

开散列表的删除操作

例 1：设关键码集合{47, 7, 29, 11, 16, 92, 22, 8, 3}，散列表表长为 11，散列函数为H(key)=key mod 11，用拉链法处理冲突构造开散列表，删除元素 47。

int HashTable2 :: Delete(int k)
{
    int j = H(k);    
    Node<int> *p = ht[j], *pre = nullptr; 
    while ((p != nullptr) && (p->data != k) 
    {
        pre = p;  p = p->next;
    }
    if (p != nullptr) {
        if (pre == nullptr) ht[j] = p->next;
        else pre->next = p->next;
        return 1;
    } else 
        return 0;
}

闭散列表的删除操作

例 2：设关键码集合{47, 7, 29, 11, 16, 92, 22, 8, 3}，散列表表长为 11，散列函数为H(key)=key mod 11，用线性探测法处理冲突构造闭散列表，删除元素 47。

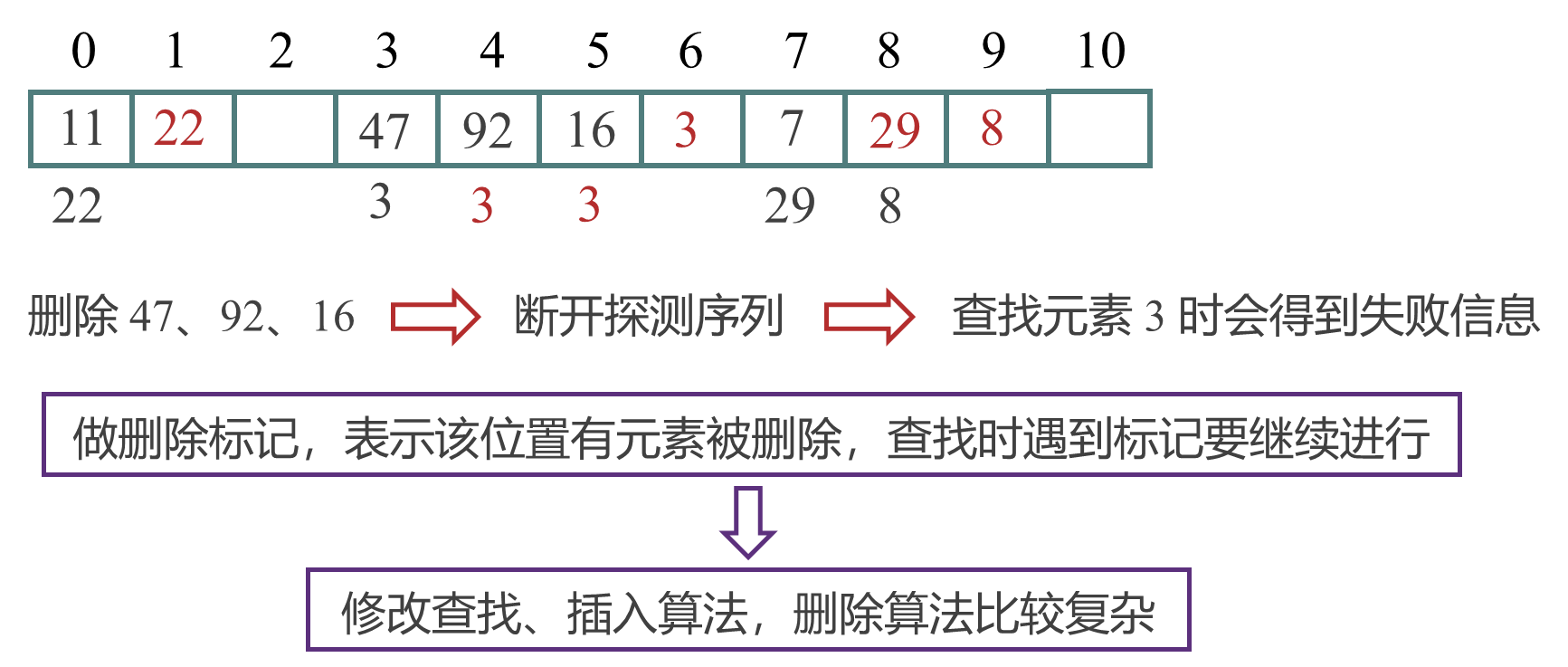
*7.5 各种查找方法的比较

顺序查找和其他查找技术相比，缺点是平均查找长度较大，特别是当查找集合很大时，查找效率较低。然而，顺序查找的优点也很突出：算法简单而且使用面广，它对表中记录的存储没有任何要求，顺序存储和链接存储均可应用；对表中记录的有序性也没有要求，无论记录是否有序均可应用。
相对于顺序查找来说，折半查找的查找性能较好，但是它要求线性表的记录必须有序，并且必须采用顺序存储。顺序查找和折半查找一般只能应用于静态查找。

与上述查找技术不同，散列查找是一种基于计算的查找方法，虽然实际应用中关键码集合常常存在同义词，但在选定合适的散列函数后，仅需进行少量的关键码比较，因此，散列技术的查找性能较高。在很多情况下，散列表的空间都比查找集合大，此时虽然浪费了一定的空间，但换来的是查找效率。

软考考点