环形链表Ⅱ 双指针 Java版本

---

题目

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。
示例 2：

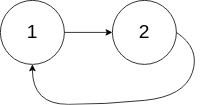
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。
示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

提示：

链表中节点的数目范围在范围 [0, 104] 内
-105 <= Node.val <= 105
pos 的值为 -1 或者链表中的一个有效索引

解题思路

设从起点到环的入口的距离为x，从入口到相遇点的距离为y，从相遇点到环的入口的距离为z
快指针步数是慢指针的二倍，所以用下图的x,y,z就可以得到一个表达式x+y+z+y=2*(x+y),表达式左侧是快指针走的步数，右侧是慢指针走的步数的二倍。
化简之后得到z=x，因此一个从起点开始走一个从相遇点开始走，两个指针再次相遇的地方就是环的入口

代码

public class Solution {
    public ListNode detectCycle(ListNode head) {
        //一个快指针一个慢指针，快指针每次走两步，满指针每次走一步
        ListNode fast=head;
        ListNode slow=head;
        while (fast!=null&&slow!=null){
            if (fast.next==null){
                return null;
            }
            fast=fast.next.next;
            slow=slow.next;
            if(fast==slow){
                //如果快慢指针相遇了，则证明有环，但是这里并不一定是相遇的地方，有可能是环内的某个位置
                //一个指针从相遇的位置出发，一个指针同时从头节点开始出发，再次相遇的时候就是环的起点
                fast=head;
                while (fast!=slow){
                    fast=fast.next;
                    slow=slow.next;
                }
                return fast;
            }

        }
        //如果已经走到null，则证明是没有环的
        return null;
    }
}