代码+视频R语言3组以上倾向评分逆概率加权(IPTW)

基于 PS （倾向评分）的IPTW 法首先由Ｒosenbaum作为一种以模型为基础的直接标准化法提出，属于边际结构模型。简单来说，就是把许多协变量和混杂因素打包成一个概率并进行加权，这样的话，我只用计算它的权重就可以了，方便了许多。那么，如何将多个协变量的影响用一个倾向评分值来表示呢? 即如何估计倾向评分值呢? 根据 Rosen-baum 和 Rubin 的定义:倾向评分值为在给定一组协变量(X i )条件下，研究对象 i(i =1，2，…N)被分配到某处理组或接受某暴露因素(Z i =1)的条件概率。理论上，所有可计算得到该条件概率的方法均可用于估计倾向评分值。

采用 logistic 回归模型估计倾向评分值具有模型
简单、容易实现、可直接得到倾向评分值、结果易于解释等显著优势。
我们拿logistic 回归做例子：
logistic 回归是最早提出的估计倾向评分值的方法，由于其原理为人们所熟悉且容易实现，也是目前最常用的估计方法。logistic 回归模型如下:

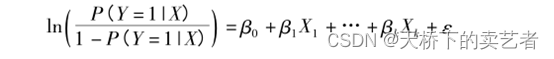
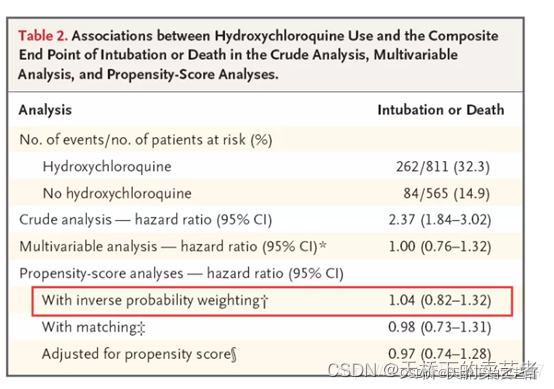
假设为二元logistic 回归，右边一系列混杂因素的方程会生成一个0-1之间的目标事件时间发生的概率，概率越大代表事件发生的可能性越大，这样就等于把多个混杂因素做成了一个综合评分来表示。用1除以这个概率就会得到一个权重，所以就叫做逆概率加权，逆概率加权（IPTW）是利用倾向性评分的倒数来处理数据间混杂的一种方法。Robins等给出的加权系数(形)计算方法是：处理组观察单位的权数Wt=1／PS，对照组观察单位的权数Wc=1／(1一PS)。PS为观察单位的倾向评分值。但此方法得到的人群往往与原来人群的数量不同，因此虚拟人群各变量的方差大小可有变化，而且有较低 PS 的处理组对象与有较高 PS 的非处理组对象将会获得很大的权重。由于非常大的权重会诱导不稳定性。Heman等人对计算方法进行调整，将整个研究人群的处理率和非处理率加入公式调整后得到稳定权数(stabilized weights)。具方法是：处理组观察单位的权数Wt=Pt／PS，对照组观察单位的权数Wc=(1–Pt)／(1–PS)。 目前蛮多文章使用稳定权重。
综上所述：倾向评分加权法首先将多个主要混杂变量的信息综合为一个变量倾向评分 ,然后将倾向评分作为需要平衡的混杂因素 ,通过标准化法的原理加权,使各对比组中倾向评分分布一致 ,则达到使各混杂因素在各比较组分布一致的目的。
下图所示，经过处理后，各项数据的分布基本上被配平了，更有利于做时候比较分析，有点起到RCT的效果。

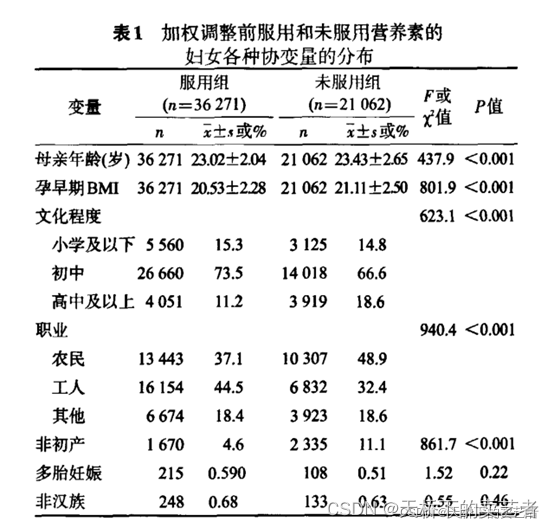
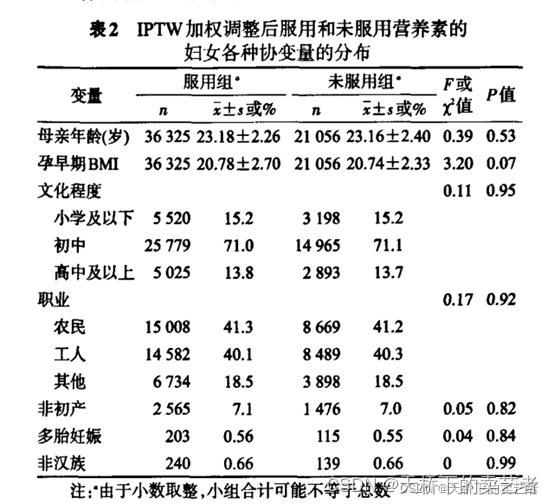
既往我们已经演示了R语言进行倾向评分逆概率加权（IPTW）。后台有粉丝问，怎么使用R进行3组以上的倾向评分逆概率加权（IPTW），看了上面内容我们就明白，只要知道每组数据的倾向评分（也就是概率），根据公式转成权重数就可以了，和做两组的步骤基本一样，今日咱们来演示一下语言3组以上倾向评分逆概率加权(IPTW)。

代码：

#导入数据
bc<-read.csv("E:/r/test/zaochan.csv",sep=',',header=TRUE)
bc <- na.omit(bc)

# 这是一个关于早产低体重儿的数据（公众号回复：早产数据，可以获得该数据），低于2500g被认为是低体重儿。
# 数据解释如下：low 是否是小于2500g早产儿，age 母亲的年龄，lwt 末次月经体重，race 种族，
# smoke 孕期抽烟，ptl 早产史（计数），ht 有高血压病史，ui 子宫过敏，ftv 早孕时看医生的次数bwt：新生儿体重数值

#分类变量转成因子
bc$race<-ifelse(bc$race=="black",1,ifelse(bc$race=="white",2,3))
bc$smoke<-ifelse(bc$smoke=="nonsmoker",0,1)
bc$low<-factor(bc$low)
bc$race<-factor(bc$race)
bc$ht<-factor(bc$ht)
bc$ui<-factor(bc$ui)

# 假设我们想比较不同种族对生早产低体重儿有无影响，
# 我们先建立没有加权的模型看看，在这里设定种族中1是黑人，2是白人，3是其他人种。

fit<-glm(low ~ age + lwt + race + smoke + ptl + ht + ui + ftv,
         family = binomial("logit"),
         data = bc)
summary(fit)
exp(confint(fit))
exp(coef(fit))  #race2：0.2803461  白人

library(ipw)
# exposure这里放入结局变量，也就是你要分组的变量。
# 3分组的话对应的family是multinomial，如果二分组对应的family是binomial，
# 如果是连续数据对应的family是gaussian。Numerator这里填入权重的分子，
# 如果按照Robins的算法这里填入1，属于不稳定权重，denominator这里吧需要调整的变量填入就可以了。

w1 <- ipwpoint(
  exposure = race,
  family = "multinomial",
  numerator = ~ 1,
  denominator = ~age + lwt+ smoke + ptl + ht + ui + ftv,
  data = bc)



#生成权重后我们把它提到数据里
bc$w1<-w1$ipw.weights

fit1.IPTW<-glm(low ~ age + lwt + race + smoke + ptl + ht + ui + ftv,family = binomial("logit"),data = bc,weights = w1)
summary(fit1.IPTW)
exp(confint(fit1.IPTW))
exp(coef(fit1.IPTW))