机器学习-KNN算法

一、k-近邻算法

• 通过计算距离来判断样本之间的相似程度

• 距离越近两个样本约相似，就可以规划到一个类别中

二、KNN算法思想

如样本在特征空间中的k个最相似的样本中的大多数属于一个类别，则该样本也属于这个类别。

k值：通过离该样本最近的K个样本(欧式距离最小的K个)。

• 比如当K = 3时, 我们就选择离这个样本最近的3个样本

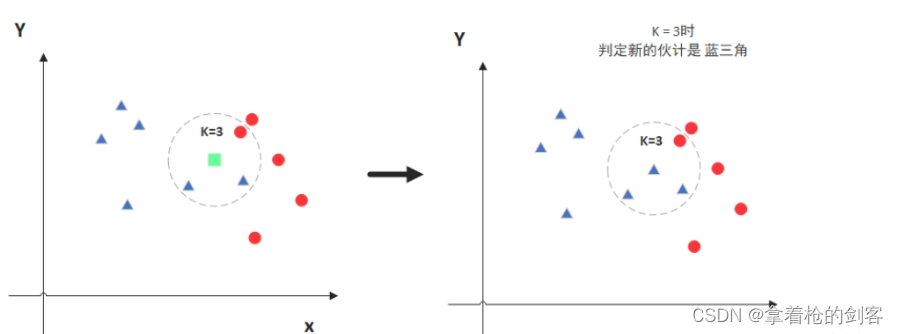
k值的影响

当k值过小时：

• 容易受到数据中噪声的影响

• 模型越复杂

当k值过大时：

• 容易受到数据分布的影响

• 模型变得简单，k等于样本个数时，新加入的所有样本值会变成一样的

KNN算法解决问题：分类问题、回归问题。

分类问题：如文本分类、图像分类等，通过比较待分类数据与已知数据点之间的相似性，KNN可以将新的数据分配到最相似的类别中。

回归问题：如房价预测、股票预测等，通过计算最近邻数据点的平均值，KNN可以以预测代分类数据的数值属性。

分类流程：

1. 计算未知样本到每一个训练样本的距离

2. 将训练样本根据距离大小升序排序

3. 取出距离最近的K个训练样本

4. 进行多数表决，统计K个样本中那个类别的样本个数最多

5. 将未知的样本归属到出现次数最多的类别

回归流程：

1. 计算未知样本到每一个训练样本的距离

2. 将训练样本根据距离大小升序排序

3. 取出距离最近的K个训练样本

4. 把这个K个样本的目标值计算其平均值

5. 作为将未知的样本预测的值

案例一(分类问题)：

#导包
from sklearn.neighbors import KNeighborsClassifier,KNeighborsRegressor
#特征值
x = [[0,2,3], [2,6,4],[1,5,8],[7,2,8],[3,4,1]]
#目标值
y = [0,0,1,1,1]
#创建算法对象，k近邻的分类器
knn = KNeighborsClassifier(n_neighbors=2)
#算法模型对象，调用fit模型训练
knn.fit(x, y)
#使用训练好的模型进行预测
knn.predict([[1,1,4]])

案例二(回归问题)：

#特征值
x = [[0,2,3], [2,6,4],[1,5,8],[7,2,8],[3,4,1]]
#目标值
y = [1,2,3,4,5]
#创建算法对象，k近邻的回归器
knn = KNeighborsRegressor(n_neighbors=2)
#算法模型对象，调用fit模型训练
knn.fit(x, y)
#使用训练好的模型进行预测
knn.predict([[1,3,0]])

三、距离的计算

欧氏距离：两点之间的直线距离。

曼哈顿距离： 也称为“城市街区距离”(City Block distance)，曼哈顿城市特点：横平竖直。

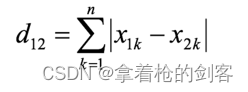
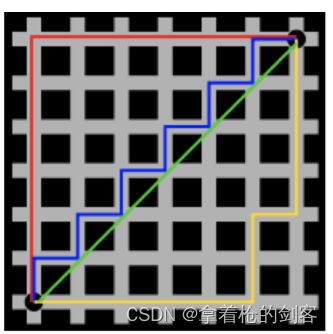
切比雪夫距离：国际象棋中，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻8个方格中的任意一个。 国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？这个距离就叫切比雪夫距离。

闵可夫斯基距离 多种距离的总的表示公式

• p = 1 曼哈顿

• p = 2 欧氏距离

• p = ∞ 切比雪夫距离

• sklearn KNN API 默认使用的是欧式距离

四、特征预处理

• 为什么要做归一化和标准化

特征的单位或者大小相差比较大，或者某个特征的方差相比其他的特征要大出几个数量级，容易影响目标结果，使得一些模型无法学习到其他的特征。

特征缩放

归一化：

• 如果出现异常点，影响了最大值和最小值，结果会发生改变

• 适合传统精确小数据的场景

标准化：

• 如果出现异常点，少量的异常点对于平均值的影响不大

• 适合现代嘈杂大数据场景

归一化

#导包，处理后的值在[0,1]之间
from sklearn.preprocessing import MinMaxScaler
#数据
x = [[90, 2, 10, 40], [60, 4, 15, 45], [75, 3, 13, 46]]
#创建对象
scaler = MinMaxScaler()
#计算每列的最大值和最小值，保存到对象中
scaler.fit(x)
#利用上一步计算出来的 最大最小值, 作用到原始数据上, 得到缩放之后的结果
scaler.transform(x)

标准化

#导包，标准化没有固定的取值范围
from sklearn.preprocessing import StandardScaler
#数据
x = [[90, 2, 10, 40], [60, 4, 15, 45], [75, 3, 13, 46]]
#创建对象
scaler = StandardScaler()
#计算每列的均值和方差
scaler.fit(x)
#利用上一步计算出来的均值和方差, 作用到原始数据上, 得到缩放之后的结果
scaler.transform(x)

五、KNN算法：鸢尾花案例

#导包
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
import pandas as p
import seaborn as sns
?
#加载数据集
iris = load_iris()
#特征名字
iris.feature_names
#目标值
iris.target_names
#特征数据
iris.data
#目标值数据
iris.target
#return_X_y=True 只会返回特征值和目标值
X, y = load_iris(return_X_y=True)
?
#数据可视化，散点图
iris_df = p.DataFrame(iris.data, columns=iris.feature_names)
iris_df['label'] = iris.target
iris_df
# hue 传入类别型取值的特征列  fit_reg默认生成一条直线
sns.lmplot(data=iris_df, x='sepal length (cm)', y='petal length (cm)', fit_reg=False, hue='label')
?
?
# X 数据集的特征， y 数据集的目标，test_size 测试集的比例， random_state 随机数种子
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=21)
#特征工程 标准化
scaler = StandardScaler()
#计算均值 方差
scaler.fit(X_train)
#标准化计算，测试集使用训练集的结果
X_train_scaler = scaler.transform(X_train)
X_test_scaler = scaler.transform(X_test)
iris_df
#模型训练
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train_scaler, y_train)
#用训练好的模型对训练集和测试集进行分类
y_train_pred = knn.predict(X_train_scaler)
y_test_pred = knn.predict(X_test_scaler)
#准确率，和真实标签进行比较。
accuracy_score(y_train, y_train_pred)
accuracy_score(y_test, y_test_pred)

数据散点图