8.1分发饼干（LC455-E）

算法：

局部最优：大尺寸的饼干既可以满足胃口大的孩子也可以满足胃口小的孩子，那么就应该优先满足胃口大的。局部最优就是大饼干喂给胃口大的，充分利用饼干尺寸喂饱一个。

全局最优：喂饱尽可能多的小孩。

为什么局部最优能推出全局最优？

贪心算法没必要用数学方法去证明，如果想不出明显的反例，那就用贪心算法试试好了。

举个例子理解：

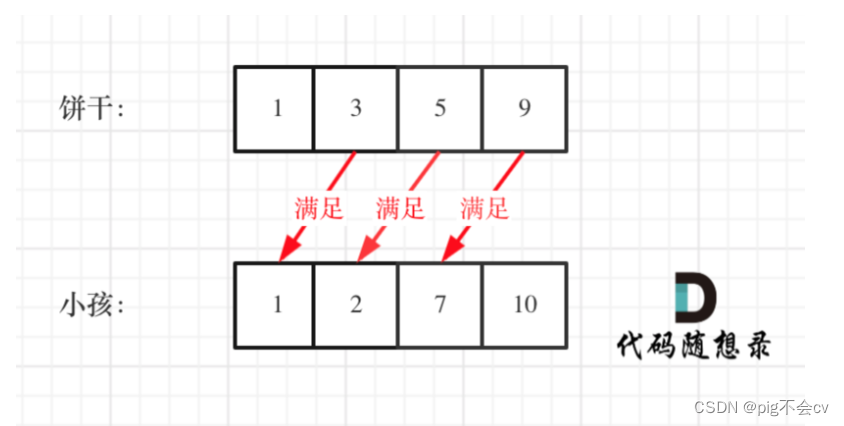
这个例子可以看出饼干 9 只有喂给胃口为 7 的小孩，这样才是整体最优解（输出3），并想不出反例，那么就可以撸代码了。

代码思路：

1.先把g和s排序

局部最优是大饼干喂给胃口大的，那怎么找出哪个大呢？所以要先排序！

2.要遍历胃口和饼干，那就要用for循环

注意顺序：先遍历胃口g（for循环），再遍历饼干s（在for循环里用if控制），若s[i] >= g[i]，则满足一个输出，结果result++

可不可以 先遍历 饼干，再遍历胃口呢？

不可以。

试一下，如果 for 控制的是饼干， if 控制胃口，就会出现如下情况 ：

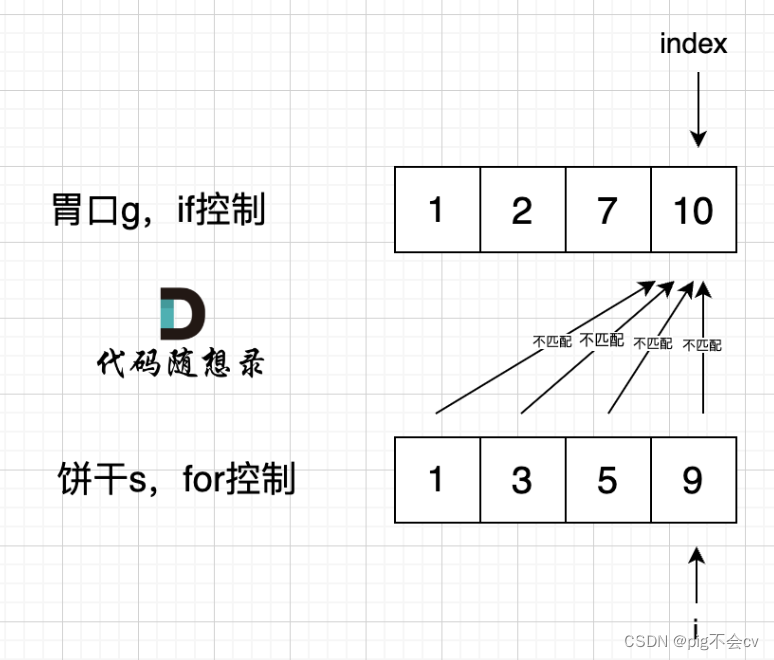
if 里的 index 指向 胃口 10， for 里的 i 指向饼干 9，因为 饼干 9 满足不了 胃口 10，所以 i 持续向前移动，而 index 走不到s[index] >= g[i]?的逻辑，所以 index 不会移动，那么当 i 持续向前移动，最后所有的饼干都匹配不上。

所以 一定要 for 控制 胃口，里面的 if 控制饼干。

调试过程：

第一次调试：

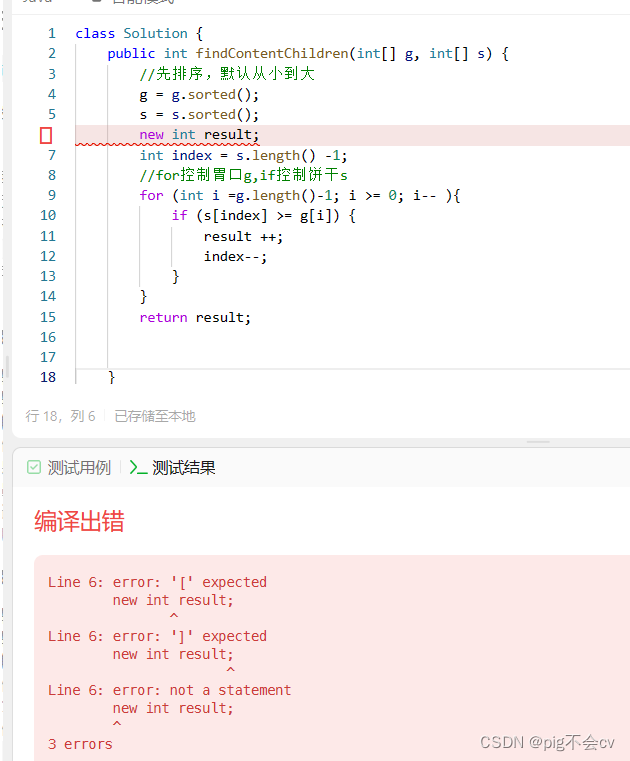
原因：

int result初始化没有赋值。

????????int result = 0;

int类型的length是属性，不用括号；而String的length是方法，需要括号

????????s.length

????????g.length

在 Java 中，数组并没有名为?`sorted`?的方法。要对数组进行排序，可以使用?`Arrays.sort`?方法。

????????Arrays.sort(g);

????????Arrays.sort(s);

第二次调试：

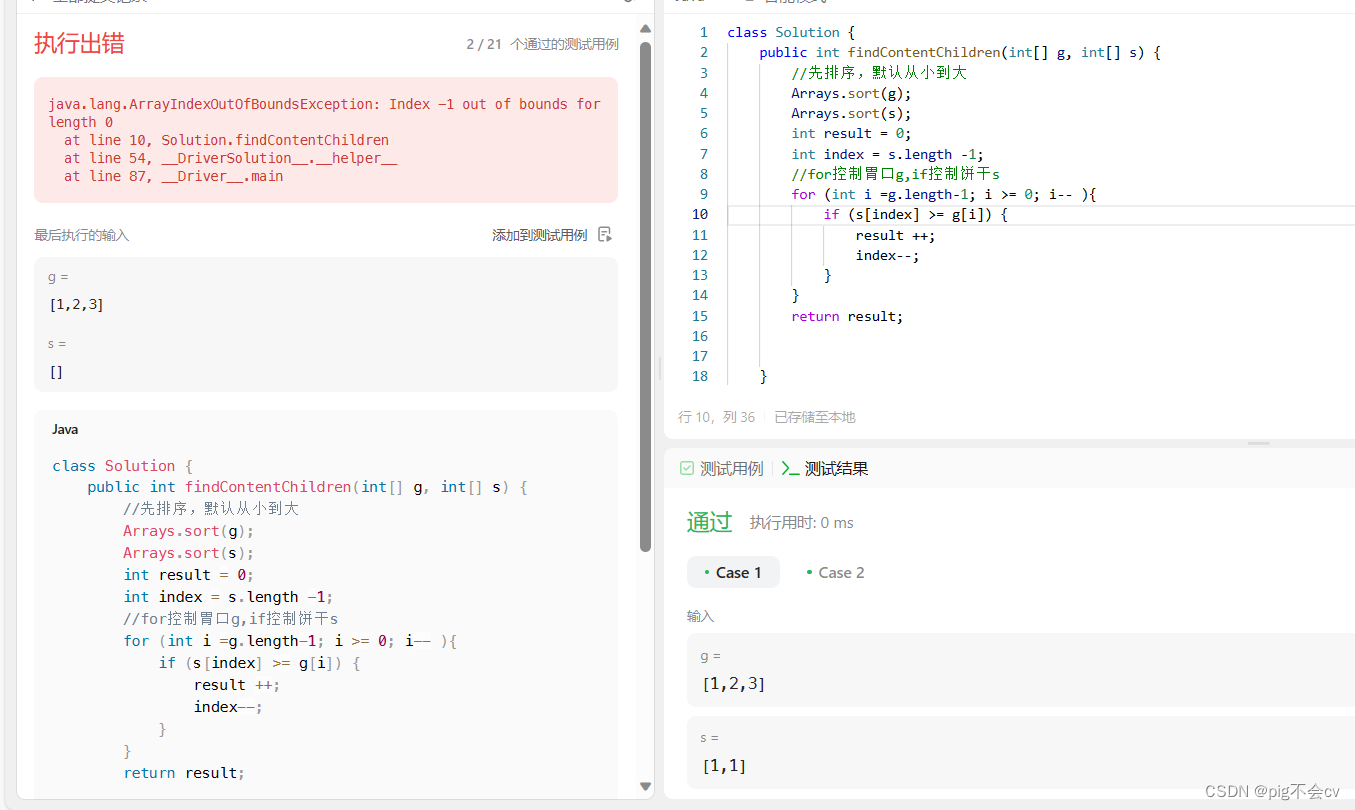
原因：

在写s[index] >= g[i]时，index不一定合法，比如s为空时，index=-1，为负值，无法作为索引

所以应改为：

if (index >=0 && s[index] >= g[i]) 

正确代码：

class Solution {
    public int findContentChildren(int[] g, int[] s) {
        //先排序，默认从小到大
        Arrays.sort(g);
        Arrays.sort(s);
        int result = 0;
        int index = s.length -1;
        //for控制胃口g,if控制饼干s
        for (int i =g.length-1; i >= 0; i-- ){
            if (index >=0 && s[index] >= g[i]) {
                result ++;
                index--;
            }
        }
        return result;


    }
}

时间空间复杂度：

时间复杂度分析

• 排序数组?`g`?和?`s`?的时间复杂度为O(nlog?n)，其中?n?是数组的长度。
• 遍历数组?`g`?的时间复杂度为?O(n)，其中?n?是数组的长度。
• 在最坏的情况下，我们需要遍历数组?`g`?一次，因此总体时间复杂度为O(nlog?n)。

空间复杂度分析

• 算法的空间复杂度为?O(1)，因为它只使用了常数级别的额外空间来存储一些变量，与输入的规模无关。