伴随矩阵定义和计算

发布时间：2024年01月12日

一、伴随矩阵定义

1）代数余子式

$A{ij} = (-1)^{i+j} * M_{ij}$

代数余子式也很好理解，在余子式的基础上多了一个-1的次方而已。

2)余子式

$M_{ij}$ ?

余子式很好理解，就是除了这个元素，出去该行该列剩下的行列式的值。

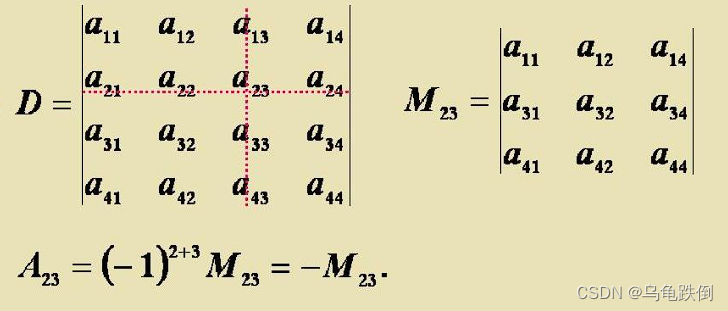
求每个元素的代数余子式，按行求，按列放。也就是说按照原位置求出每个元素的代数余子式之后，还需要转置。

任意矩阵都有伴随矩阵，很好理解，因为对于每个矩阵的每一个元素都可以求其代数余子式，也就自然一定存在伴随矩阵。

二、核心公式

AA = AA = |A|E

$\left | A^{*} \right | = \left | A \right |^{n-1}$ ?

$\left | A^{*}A \right | = \left | A^{*} \right | \left |A \right |$

$\left | \left | A \right |E \right | = \left | A \right |^{n} \left | E \right | = \left | A \right |^{n}$