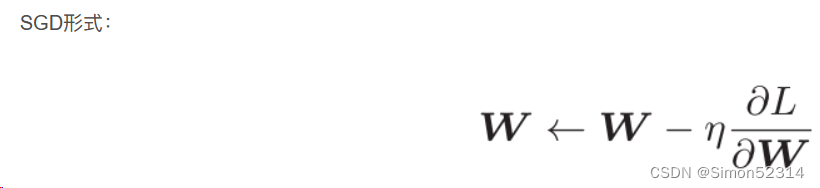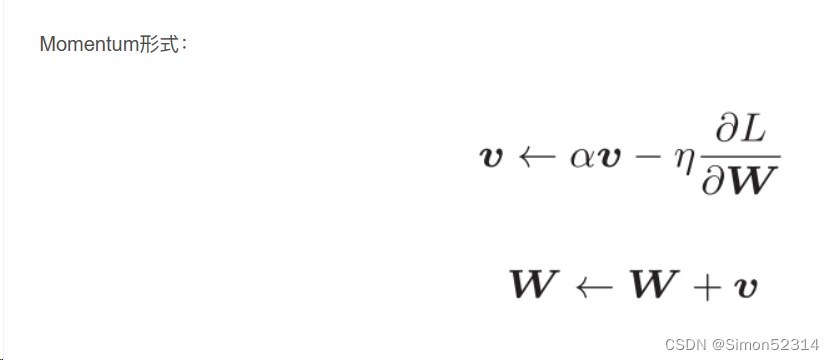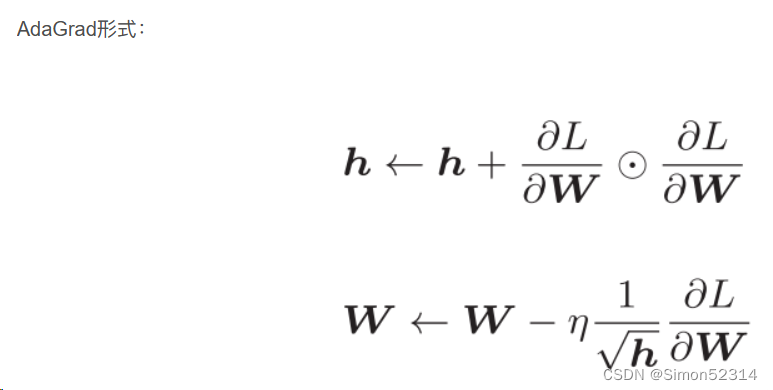优化算法2D可视化的补充

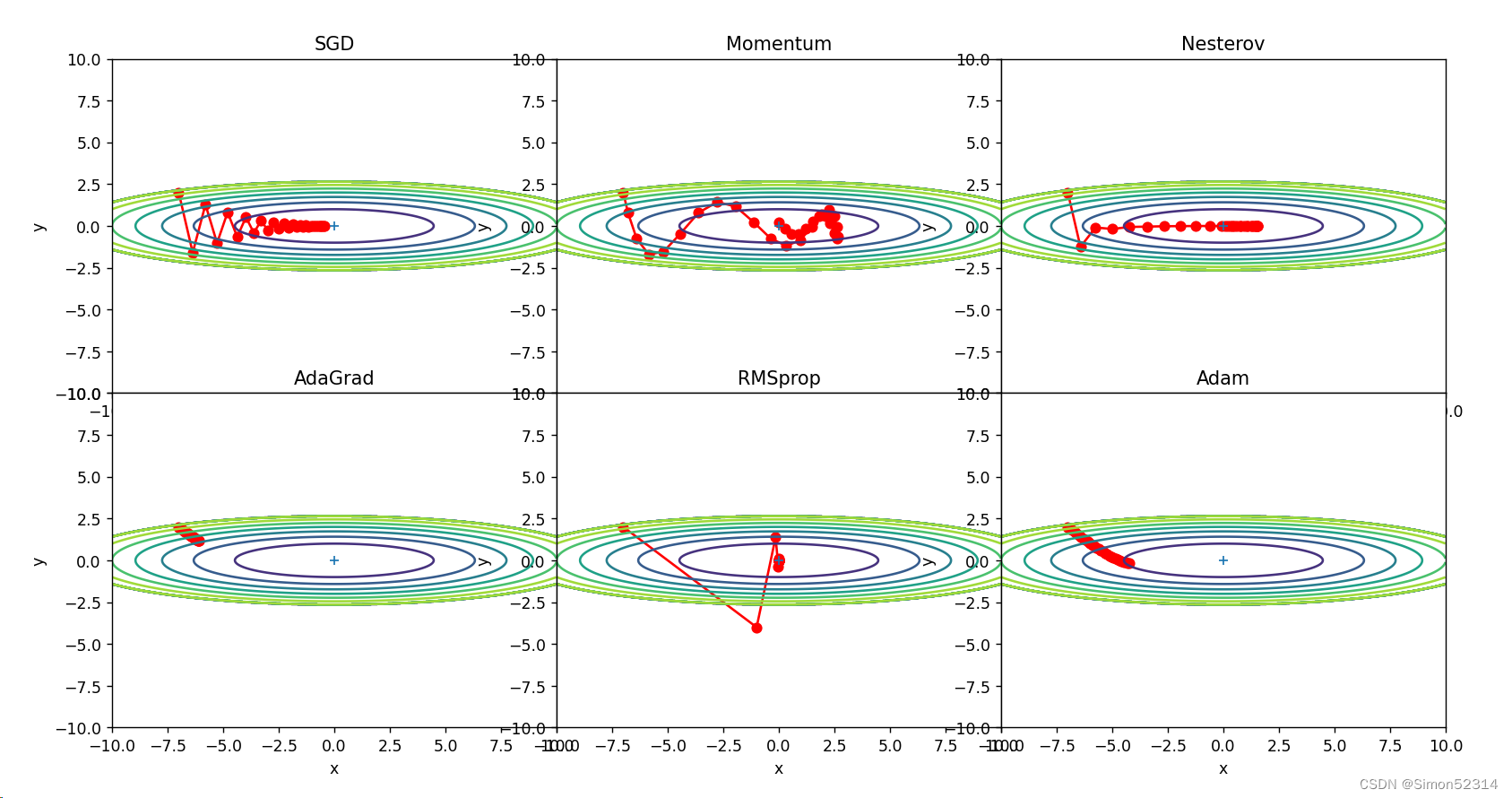
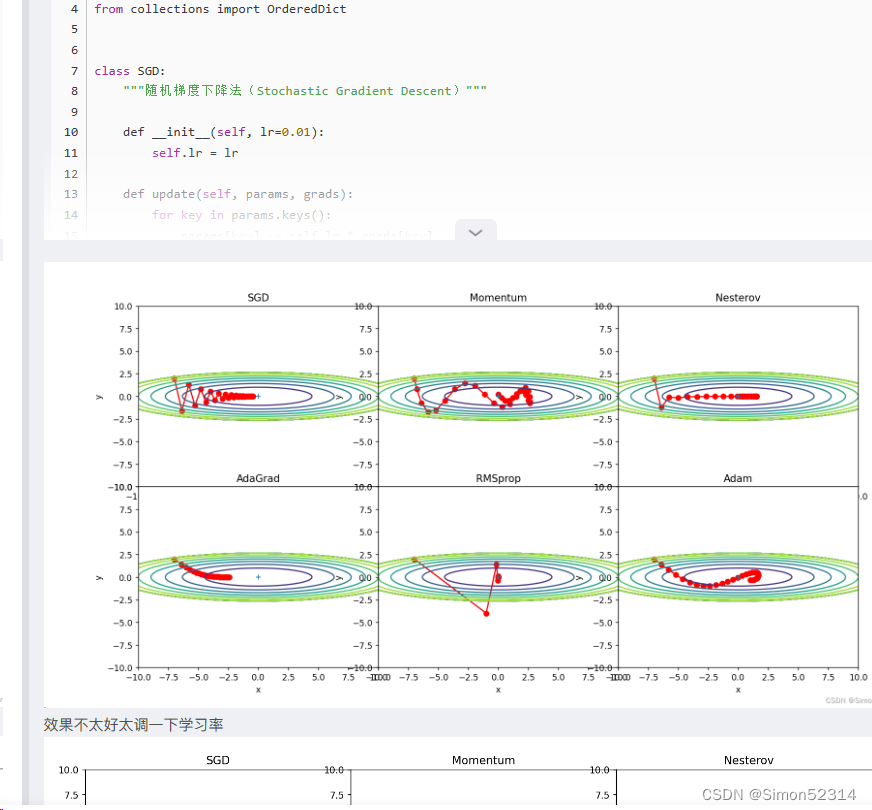
4. 分析上图，说明原理（选做）

1、为什么SGD会走“之字形”？其它算法为什么会比较平滑？

? ? ? 之所以会走"之字形"，是因为它在每次更新参数时只考虑当前的样本梯度。这导致参数更新非常不稳定，每个样本的梯度方向不一致，从而产生了"之字形"的更新路径。

? ? ?其他算法相对比较平滑的原因是它们引入了不同的策略来平衡参数更新的稳定性和速度。

例如，Momentum算法引入了动量概念，它在更新参数时考虑了之前更新的方向和速度。通过积累之前梯度的指数衰减平均值，动量算法可以在梯度方向一致时加速收敛，并减少参数更新的震荡，从而使得更新路径更加平滑。Adagrad和RMSprop算法引入了自适应学习率的概念。它们通过梯度的历史信息对学习率进行调整，可以根据梯度值的大小对参数的不同方向分配不同的学习率。这样可以使得梯度大的方向学习率减小，梯度小的方向学习率增大，从而更加平滑地更新参数。Adam算法在Momentum和RMSprop的基础上进一步改进，结合了二者的优点。Adam算法不仅考虑了动量对更新路径的影响，还引入了关于梯度平方的一阶矩量和二阶矩量的估计，通过对梯度的偏移和峰值信息进行动态调整，进一步提高更新路径的平滑性。

2、Momentum、AdaGrad对SGD的改进体现在哪里？速度？方向？在图上有哪些体现？

? ? Momentum算法在更新时，引入了动量的概念，考虑了之前梯度更新的方向和速度。通过积累之前梯度的指数衰减平均值，动量算法可以在梯度方向一致时加速收敛，并减少参数更新的震荡。它在速度方面对SGD的改进的体现在:相当于增加了更新方向的平滑性。在图上，这个改进体现为更新路径会比SGD更加平滑，能够加速收敛。

??

? ? ?Adagrad，它通过历史梯度信息对每个参数自适应地调整学习率。Adagrad的学习率随着时间步的增加而不断衰减，在每个参数那里都单独调整。这对于处理非平稳、强烈相关的数据具有很好的效果。在速度方面对SGD的改进的体现在：可以自适应地调整每个参数的学习率，以更贴合各自的梯度，能够让更新更快速及早达到收敛。在图上，这个改进体现为更新路径更加平缓而且每个维度更新幅度差异不大。

3.仅从轨迹来看，Adam似乎不如AdaGrad效果好，是这样么？

? ?轨迹上来看，是这样，因为此时Adam和AdaGrad的学习率并不相同，并且Adam和AdaGrad选择的均是一个恰当的学习率。

但是图中的学习率都是调整过的，我们随机换一个相同的学习率(0.1)

由上可见：Adam优于Adagrad

所以上述观点错误，没有一个模型会永远由于另一个，知识参数不对而已。

5、调整学习率、动量等超参数，轨迹有哪些变化？

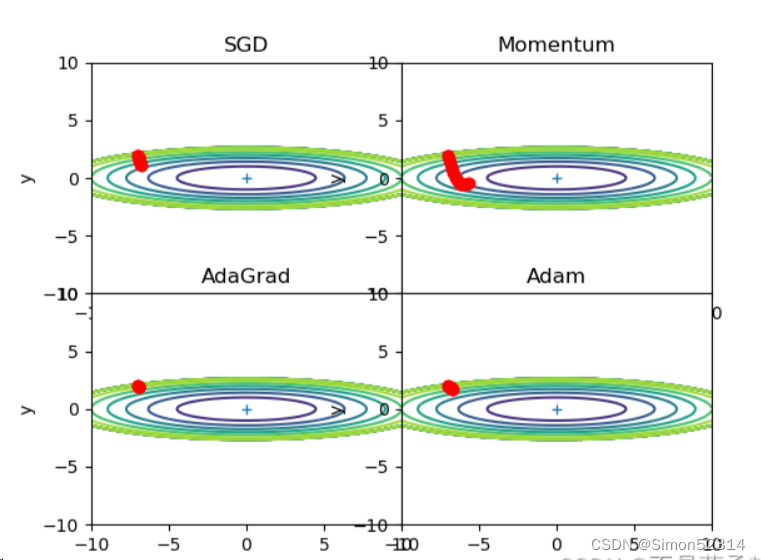
lr=0.01时：

?lr太小，30次根本不够搜索的，改为1000次

这次Momentum找到了最小点，Adam马上找到，而其他两种算法还差得多

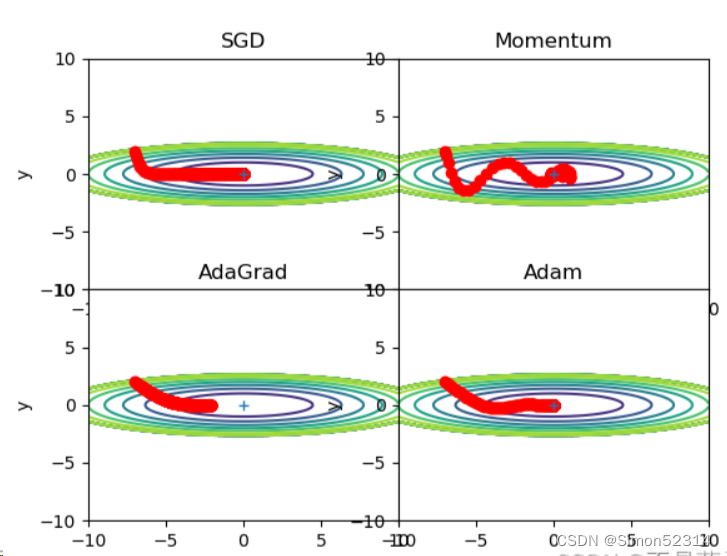
lr=0.1，搜索1000次

只有AdaGrad没有找到最小点?

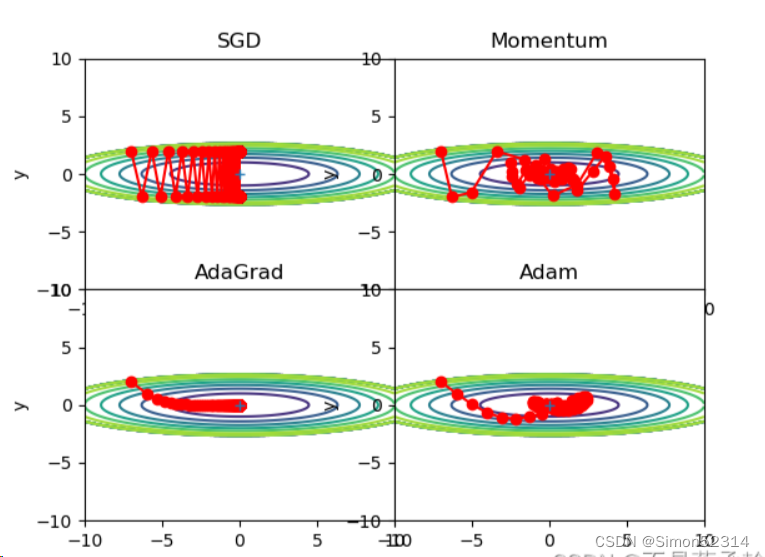
?lr=1，搜索1000次

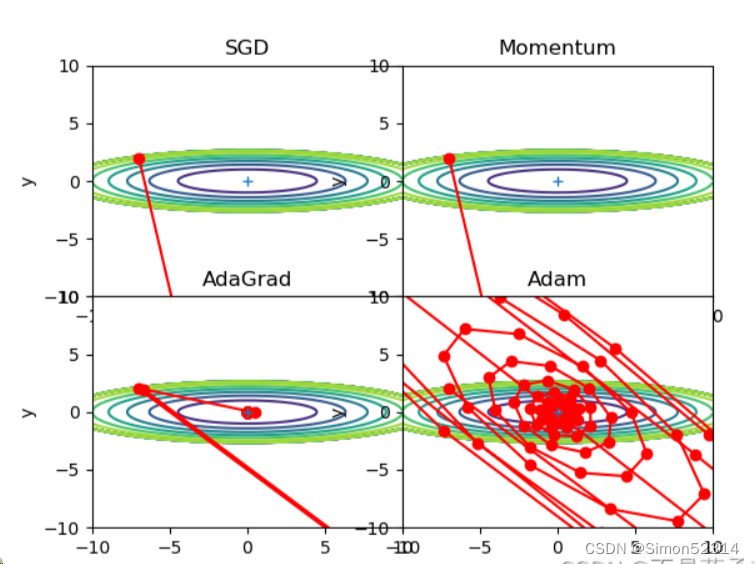
r=100，搜索100次?

?可以发现，SGD和Momentum很容易错过全局最小值，Adam需要较长的时间和较多的搜索次数来找到全局最小值，AdaGrad效果最好。

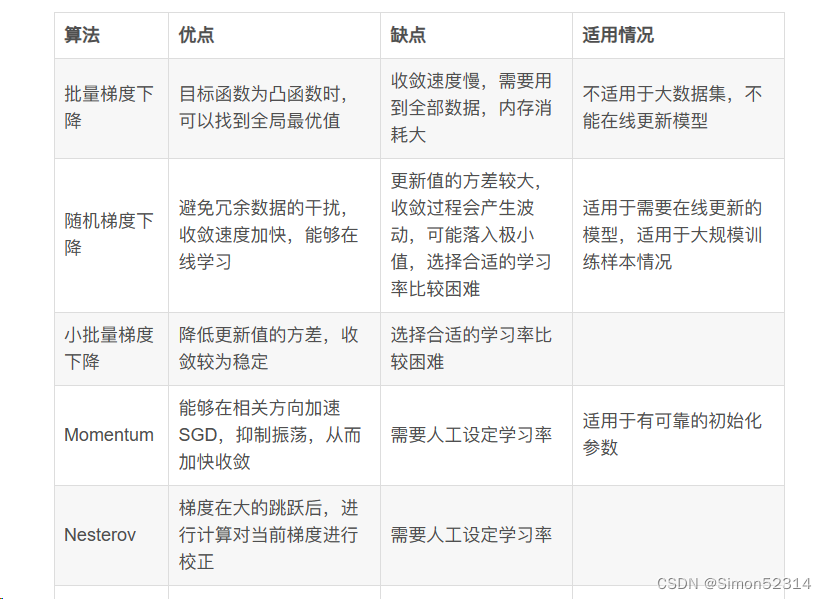
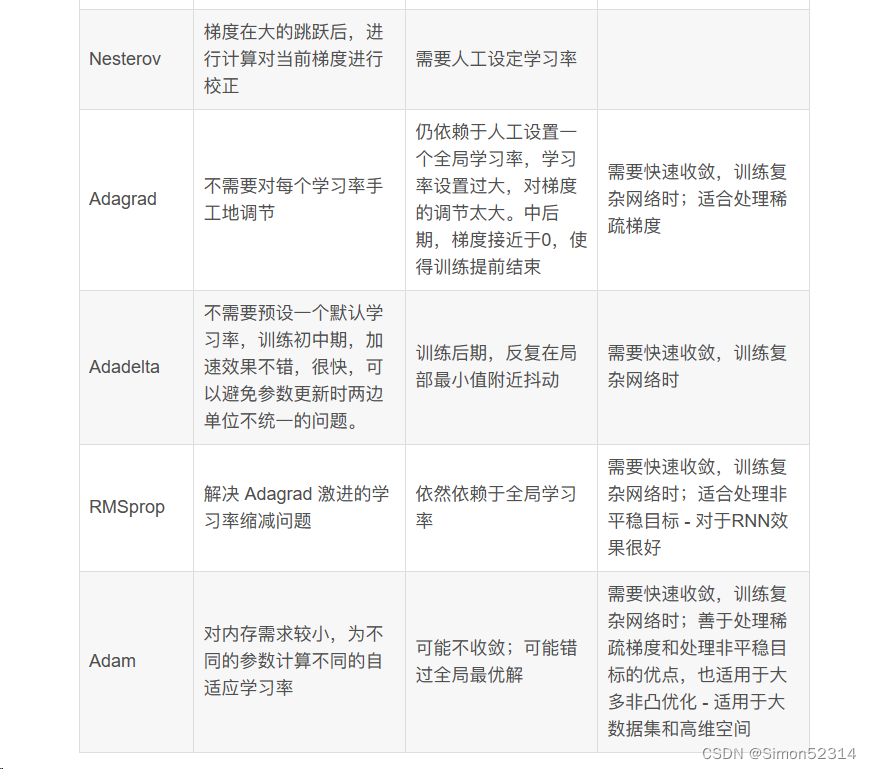
5. 总结SGD、Momentum、AdaGrad、Adam的优缺点

上个博客有

但是我发现学长总结更直观

6. Adam这么好，SGD是不是就用不到了？?

? ? SGD最大的缺点是下降速度慢，而且可能会在沟壑的两边持续震荡，停留在一个局部最优点。SGD没有用到二阶动量，因此学习率是恒定的（实际使用过程中会采用学习率衰减策略，因此学习率递减）。AdaGrad的二阶动量不断累积，单调递增，因此学习率是单调递减的。因此，这两类算法会使得学习率不断递减，最终收敛到0，模型也得以收敛。

但AdaDelta和Adam则不然。二阶动量是固定时间窗口内的累积，随着时间窗口的变化，遇到的数据可能发生巨变，使得可能会时大时小，不是单调变化。这就可能在训练后期引起学习率的震荡，导致模型无法收敛。

? ?并且Adam有两大罪状

? 谈到现在，到底Adam好还是SGD好？这可能是很难一句话说清楚的事情。去看学术会议中的各种paper，用SGD的很多，Adam的也不少，还有很多偏爱AdaGrad或者AdaDelta。可能研究员把每个算法都试了一遍，哪个出来的效果好就用哪个了。

? ? ? 而从这几篇怒怼Adam的paper来看，多数都构造了一些比较极端的例子来演示了Adam失效的可能性。这些例子一般过于极端，实际情况中可能未必会这样，但这提醒了我们，理解数据对于设计算法的必要性。优化算法的演变历史，都是基于对数据的某种假设而进行的优化，那么某种算法是否有效，就要看你的数据是否符合该算法的胃口了。

7. 增加RMSprop、Nesterov算法

上个博客有

对比Momentum与Nesterov

两个算法都是动量优化法，Nesterov项是momentum的改进，在梯度更新时做一个校正，让之前的动量直接影响当前的动量，避免前进太快，同时提高灵敏度。

对比AdaGrad与RMSprop

两个都是自适应学习率优化法，RMSprop解决了对历史梯度一直累加而导致学习率一直下降的问题，适合处理非平稳目标，对于RNN效果很好，但RMSprop依然依赖于手动选择全局学习率。

8.?基于MNIST数据集的更新方法的比较

# coding: utf-8
import os
import sys

import numpy as np

from jiwang.Server import SGD, Momentum, AdaGrad, Adam

sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import matplotlib.pyplot as plt
from nndl4.dataset import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import *

# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000

# 1:进行实验的设置==========
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
# optimizers['RMSprop'] = RMSprop()

networks = {}
train_loss = {}
for key in optimizers.keys():
    networks[key] = MultiLayerNet(
        input_size=784, hidden_size_list=[100, 100, 100, 100],
        output_size=10)
    train_loss[key] = []

# 2:开始训练==========
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    for key in optimizers.keys():
        grads = networks[key].gradient(x_batch, t_batch)
        optimizers[key].update(networks[key].params, grads)

        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)

    if i % 100 == 0:
        print("===========" + "iteration:" + str(i) + "===========")
        for key in optimizers.keys():
            loss = networks[key].loss(x_batch, t_batch)
            print(key + ":" + str(loss))

# 3.绘制图形==========
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()

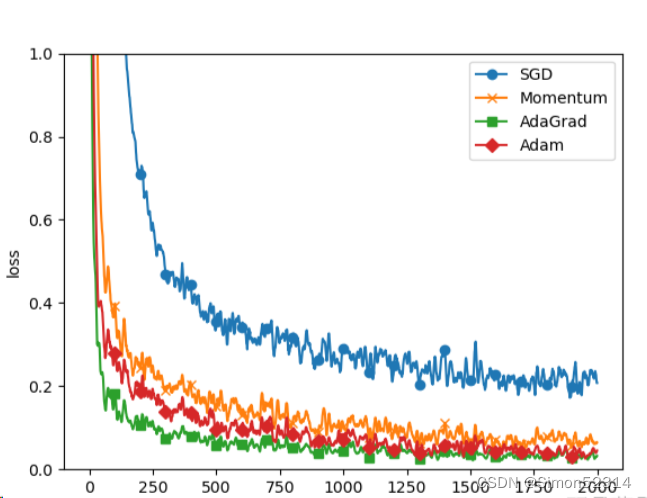
从结果中可知，与SGD相比，其他3种方法学习得更快，而且速度基本相同，仔细看的话，AdaGrad的学习进行得稍微快一点。这个实验需要注意的地方是，实验结果会随学习率等超参数、神经网络的结构（几层深等）的不同而发生变化。不过，一般而言，与SGD相比，其他3种方法可以学习得更快，有时最终的识别精度也更高。

---

总结：

1、本来觉得自己上个博客总结的还不错，看了上届学长的总结，觉得更直观，更好，直接盗了

2、每个优化算法在不同的模型上的表现是不一样的，而且会因为学习率等参数的不同，引起效果的不同。

3、今天24考研结束，作为25考研的我感觉天都黑了，没人在前面挡着了。

参考链接：

NNDL 作业11：优化算法比较_基于mnist数据集的更新方法-CSDN博客?

NNDL 作业11：优化算法比较_"ptimizers[\"sgd\"] = sgd(lr=0.95) optimizers[\"mo-CSDN博客

HBU-NNDL 作业11：优化算法比较_adam不收敛-CSDN博客