ZKP Sigma Protocol

Sigma Protocol

Introduction

Sigma protocols are a specific type of interactive zero-knowledge proof (ZKP) that are known for their efficiency and simplicity.
They involve three distinct phases between a prover and a verifier:

• Prover: $P(x,y)$
• Verifier: $V(y)$
• Commitment: The prover sends an initial commitment $t$ to the verifier, often involving a secret value.
• Challenge: The verifier responds with a random challenge $c$.
• Response: The prover calculates a response $z$ based on the challenge and their secret knowledge and sends it to the verifier.
• Evaluation: Upon receiving prover’s response $z$, the verifier outputs either accept or reject, which must be computed strictly as a function of the statement $y$ and the conversation $(t,c,z)$. In particular, the verifier does not make any random choices other than the selection of the challenge: all other computations are completely deterministic.

Example: Okamoto’s protocol

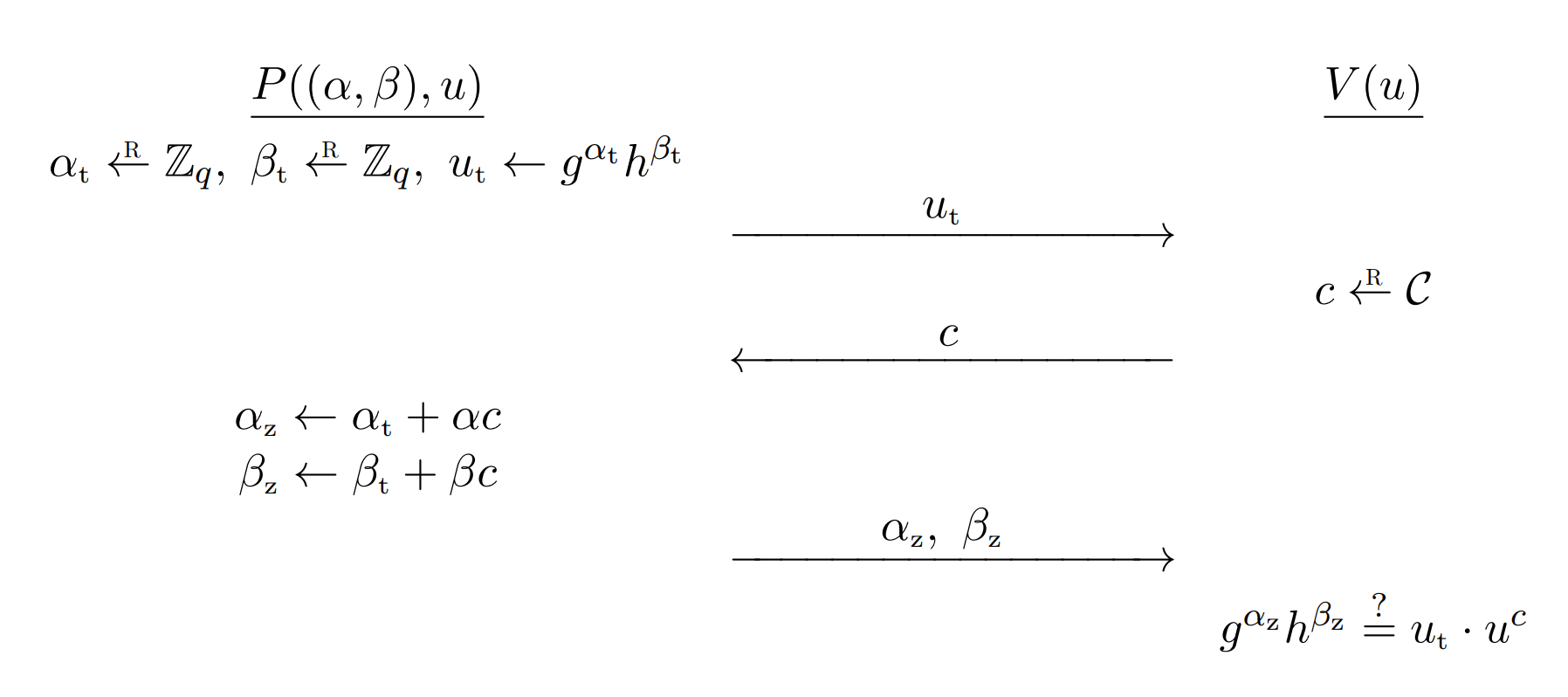
Okamoto’s protocol allows a prover to convince a skeptical verifier that he “knows” a representation of a given $u\in \mathbb{G}$, without revealing anything about that representation to the verifier.

A witness for the statement $u\in \mathbb{G}$ is $(\alpha ;\beta )\in {\mathbb{Z}}_q^2$such that $g^{\alpha }{h}^{\beta }=u$, i.e., a representation of $u$. Thus, in this example, every statement has many witnesses.

• Prover: $P((\alpha ,\beta ),u)$
• Verifier: $V(u)$
• The prover computes ${\alpha }_t\leftarrow \mathbb{G}$, ${\beta }_t\leftarrow \mathbb{G}$, $u_t\leftarrow g^{{\alpha }_t}{h}^{{\beta }_t}$ and sends the commitment $u_t$ to the verifier.
• The verifier computes a random $c$ and sends the challenge $c$ to the prover.
• The prover computes ${\alpha }_z\leftarrow {\alpha }_t+\alpha c\in {\mathbb{Z}}_q$, ${\beta }_z\leftarrow {\beta }_t+\beta c\in {\mathbb{Z}}_q$ and sends the response $({\alpha }_z,{\beta }_z)$ to the verifier.
• The verifier checks if $g^{{\alpha }_z}{h}^{{\beta }_z}=u_t?u^c$. if so, the verifier outputs “accept”; otherwise, the verifier outputs “reject”.