图文证明费马,罗尔,拉格朗日,柯西

发布时间：2024年01月01日

图文证明罗尔,拉格朗日,柯西

费马引理和罗尔都比较好证,不过多阐述,看图即可:

费马引理:

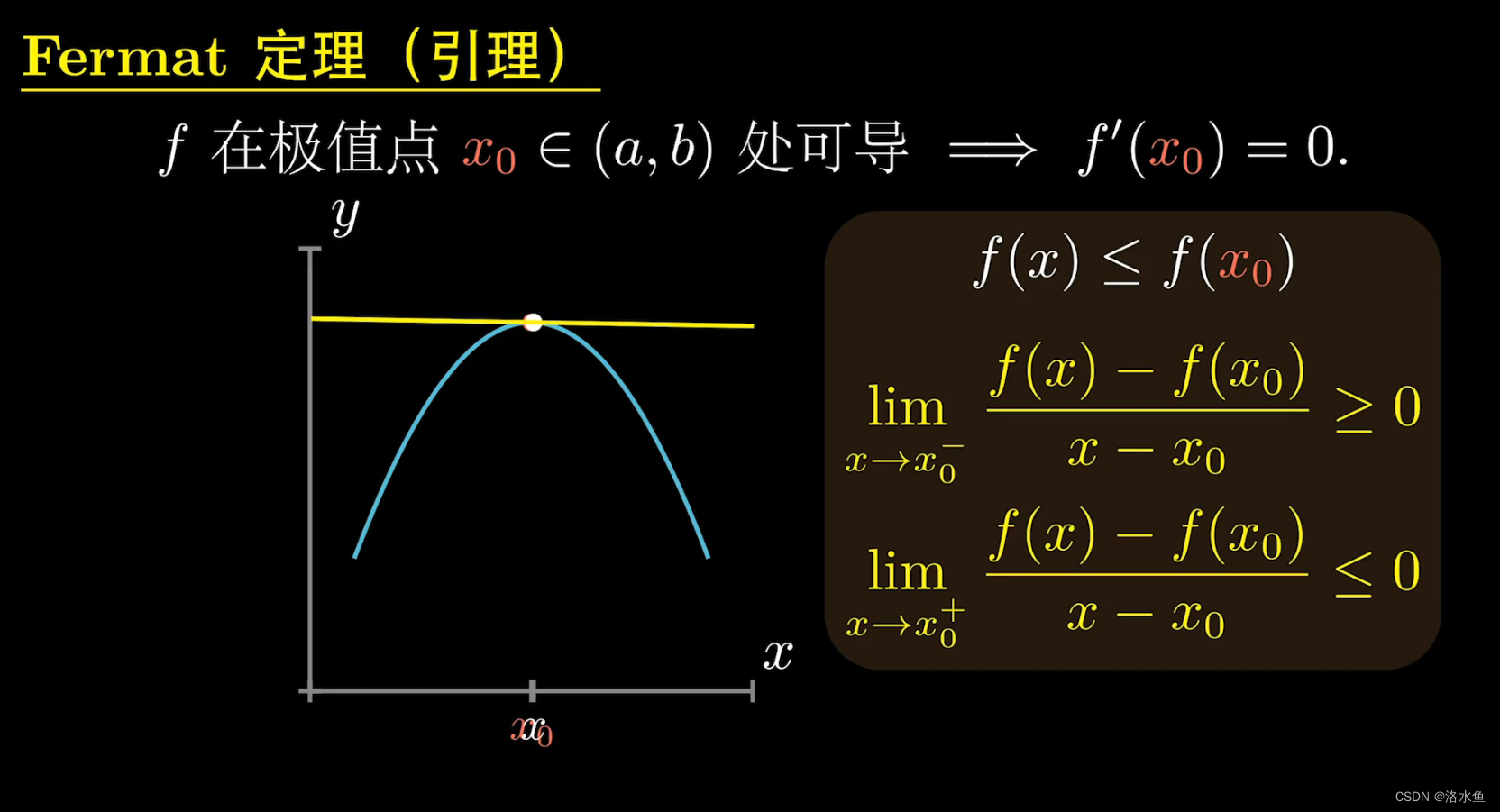
在这里插入图片描述

罗尔定理:

在这里插入图片描述
重点来证明拉格朗日和柯西

拉格朗日:

在这里插入图片描述
我认为不需要去看l(x)的那一行更好推:
详细的推理过程:

$\quad \text{因为} \; a, b \; \text{两点为交点}, \; f(a) = l(a), \; f(b) = l(b),$

$\text{所以} \; h(a) = h(b) = 0. \quad \text{根据罗尔定理}, \; \exists \, c \in (a, b) \; \text{使得} \; h'(\xi ) = 0.$

$\text{因为} \; h(\xi ) = f(\xi ) - l(\xi ), \; \text{我们有} \; h'(\xi ) = f'(\xi ) - l'(\xi ). \quad \text{因此}, \; h'(\xi ) = f'(\xi ) - l'(\xi ) = 0.$

$\text{由此得出} \; f'(\xi ) = l'(\xi ).$

$\text{根据两点式得:} \; l'(\xi ) = \frac{{f(b)-f(a)}}{{b-a}}$

$\text{由于已知} \; f'(\xi ) = l'(\xi ), \; \text{你可以使用这个信息进一步推导出} \; \ f'(x) = l'(x) = \frac{{f(b)-f(a)}}{{b-a}}.$

柯西:

在这里插入图片描述
$\text{给定两个函数} \; f(x) \; \text{和} \; g(x) \;$
$\text{在区间} \; [a, b] \; \text{上，其中} \; f(x) \neq g(x) \; \text{。根据拉格朗日中值定理，存在} \; c \in (a, b) \; \text{使得}$

$f'(\xi ) = \frac{f(b) - f(a)}{b - a}, \quad g'(\xi ) = \frac{g(b) - g(a)}{b - a}.$

$\text{现在，我们使用换元法，将} \; f'(\xi ) \; \text{的} \; (b - a) \; \text{替换为} \; \frac{g(b) - g(a)}{g'(\xi )}$

$\frac{f(b) - f(a)}{\frac{g(b) - g(a)}{g'(c)}}.$

$\text{通过简化得到} \; f'(c) = \frac{f(b) - f(a)}{g(b) - g(a)} \cdot g'(c).$

发现一个看一眼就明了的列子

拉格朗日：如果你一小时跑了5km，你的平均速度就是5km/h。那么在这一小时以内，要么一直保持5km/h，要么一部分比这个速度快，一部分比这个速度慢。在快慢转换的点，你的速度就是5km/h。

柯西：我一小时跑了5km，你一小时跑了20km。要么你的速度一直是我的20/5=4倍，要么你一部分比我四倍还快，一部分比我四倍慢，在这转换的这一点，你的速度是我的四倍。

参考视频:

罗尔、拉格朗日、柯西【中值定理】证明

文章来源:https://blog.csdn.net/L2489754250/article/details/135318792
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！

图文证明 费马,罗尔,拉格朗日,柯西