Python算法例29 统计比给定整数小的数

1. 问题描述

给定一个整数数组（数组长度为n，元素的取值范围为0~10000），以及一个查询列表。每一个查询都会给出一个整数，本例将返回数组中小于该给定整数的元素数量。

2. 问题示例

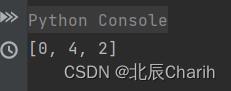
对于数组[1，2，7，8，5]，查询[1，8，5]，返回[0，4，2]。

3. 代码实现

采用线性搜索的方法实现

def count_elements(arr, queries):
    result = []
    for query in queries:
        count = 0
        for num in arr:
            if num < query:
                count += 1
        result.append(count)
    return result

# 示例测试
arr = [1, 2, 7, 8, 5]
queries = [1, 8, 5]
print(count_elements(arr, queries))

这段代码首先定义了一个count_element函数，接受一个整数数组arr和一个查询列表queries作为参数。然后，对于每个查询query，使用一个嵌套的循环遍历数组arr，统计小于该查询的元素数量，并将结果添加到结果列表result中。最后，返回结果列表。

这个算法的时间复杂度为，其中是数组长度，是查询列表的长度。由于每个查询需要遍历整个数组，所以时间复杂度较高。

使用排序和二分查找的方法实现

from bisect import bisect_left

def count_elements(arr, queries):
    arr.sort()  # 对数组进行排序
    result = []
    for query in queries:
        index = bisect_left(arr, query)  # 使用二分查找找到第一个大于等于查询值的元素的索引
        result.append(index)
    return result

# 示例测试
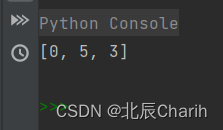
arr = [1, 2, 7, 9, 7,3]
queries = [1, 8, 5]
print(count_elements(arr, queries))

这段代码首先使用sort()函数对数组arr进行排序。然后，对于每个查询query，使用bisect_left()函数进行二分查找，找到数组中第一个大于等于查询值的元素的索引。由于数组已经有序，可以使用二分查找来提高查找效率。最后，将索引添加到结果列表result中。

这个算法的时间复杂度为，其中是数组长度，是查询列表的长度。排序的时间复杂度为，而每次二分查找的时间复杂度为。