前缀和算法模板
发布时间:2024年01月06日
一维前缀和
算法用途:快速求出数组中某一连续区间的和
一维前缀和算法模板
1、预处理出一个 dp 数组
要求原数组存储在 n + 1 的空间大小中,其中后 n 个空间存数据。
dp数组,数组开 n + 1个空间,dp[i] 表示 [ 1, i ] 区间内所有元素的和。
处理方法:? dp[ i ] = dp[ i - 1 ] + arr[ i ]?
2、使用前缀和数组
区间 l 到 r 的和:? sum = dp[ r ] - dp[ l - 1 ]?
复杂度分析
处理前缀和数组,需要 O(N) 的空间复杂度和空间复杂度,求一次区间 l 到 r 的和,需要 O(1) 的时间复杂度,如果需要求 q 次和,则时间复杂度就是 O(q) + O(N)
二维前缀和
算法用途:快速求出某个子矩阵的和
二维前缀和算法模板
1、预处理出一个 前缀和矩阵(二维数组 dp)
假设原矩阵有 m 行,n列,那么这个前缀和矩阵的二维数组 dp 要开 m+1 行, n+1 列的空间,第一行,第一列的数据都为 0,?dp[ i ][ j ] 表示 [ 1, i ]?行,[ 1, j ] 列包含的这个矩阵的数据和
处理方法:dp[ i ][ j ] = dp[ i - 1 ][ j ] + dp[ i ][ j - 1 ] - dp[ i - 1 ][ j - 1 ] + arr[ i ][ j ]
2、使用前缀和矩阵
[ x1, y1 ] ~ [ x2, y2 ] = dp[ x2, y2] - dp[ x1- 1 ][ y2 ] - dp[ x2 ][ y2?- 1 ] + dp[ x1 ][ y1 ]
二维数组前缀和的建立和使用图解

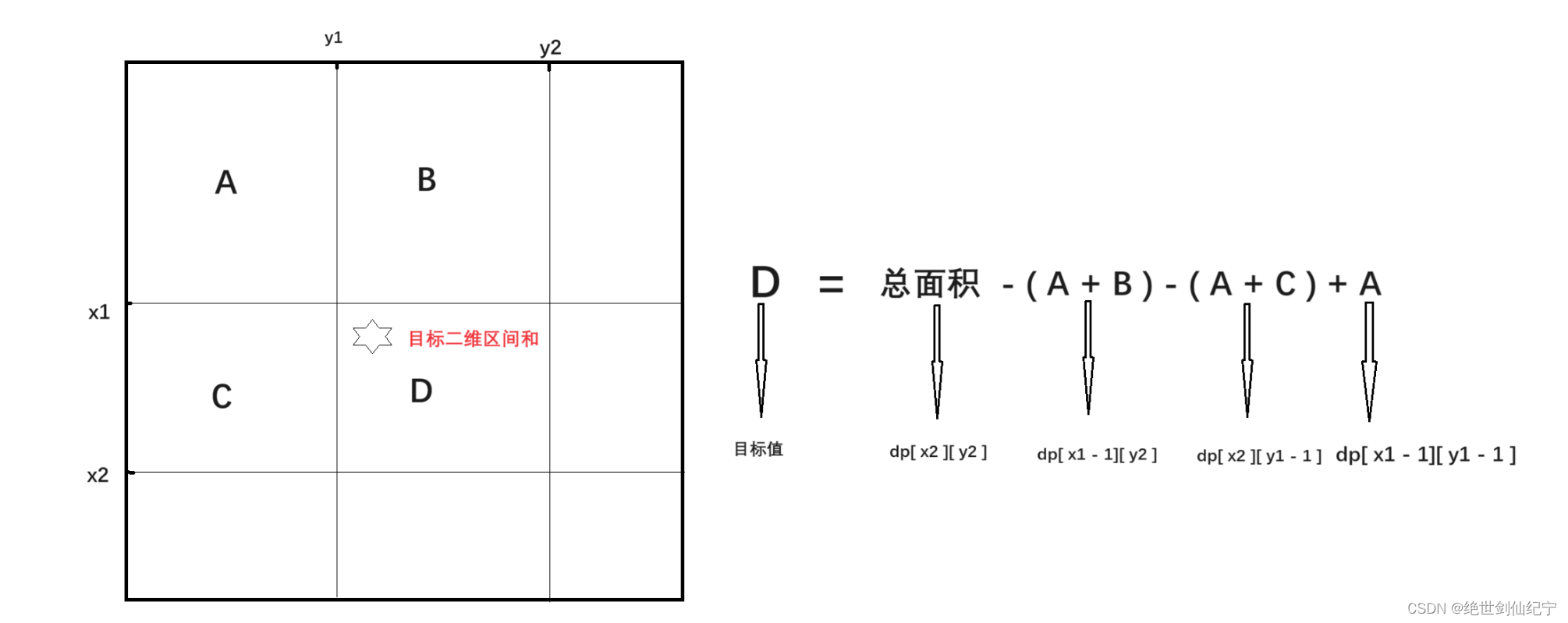 ?
?
文章来源:https://blog.csdn.net/zyb___/article/details/135419101
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- SQLite 安装与使用
- 领域驱动设计解决汉诺塔问题-文风批评(1)
- 51-14 Retentive Network,RetNet 多尺度保留机制序列建模论文精读
- 提前避坑Anzo Capital总结浮动差价的3个缺点
- 算法学习系列(十四):并查集
- nodejs搭建服务
- Python如何操作RabbitMQ实现fanout发布订阅模式?有录播直播私教课视频教程
- 【EI会议征稿】第五届机械仪表与自动化国际学术会议(ICMIA 2024)
- 09 STM32 - PWM
- Pillow和OpenCV的Python图像处理库你都用过了吗?