小白水平理解排序题目leetcode 54 Spiral Matrix (螺旋矩阵I)

54 Spiral Matrix I (螺旋矩阵 I)

题目属于Array类题目，主要用到矩阵，数组，和模拟。对于Array题目，可以暴力解法，二分查找，双指针，滑动窗口，递归算法）。

原题描述：

给定一个 m x n 矩阵，按螺旋顺序返回矩阵的所有元素。

这题一上来描述贼少，但是图型描述可不少。直接扔出两个矩阵便于广大怨种理解，好了，是难办的数据矩阵一类。遥想当年还是在大学，坐在教室后排在上着线性代数，同时看长发飘飘女同学时候。。。啪！继续看题！

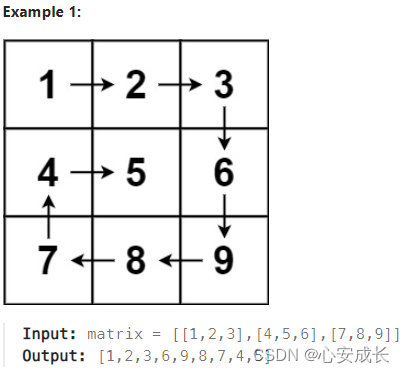
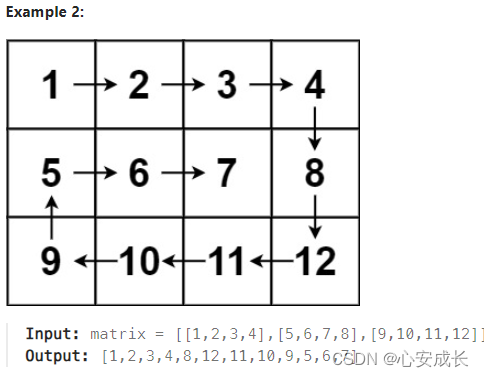
这里我个人小白理解分析：

思考1：如果只有一行，那就好办了，两维结构如何处理，第一行走到头了怎么改变方向？

思考2：第一行走到最右边时候，需要开始往下走，也就是箭头方向顺时针90°；
当走完第一行之后，剩余部分，可以继续采用顺时针旋转90°，继续遍历，这里就可以用递归解决。
这里用[r, c]记录当前位置，也就是row与column。下一个位置为[r’, c’] = [r + dr, c + dc], dr与dc分别为不同方向的行与列变化。

Index	Direction	dr	dc
0	Right	0	1
1	Down	1	0
2	Left	0	-1
3	Up	-1	0

遍历的方向为 Right ? Down ? Left ? Up

这里就又要想到那个教室线性代数课，和那个黑长直了。

数学上来说，[dr, dc]的斜率用dr/dc来表示，垂直于它的斜率则为-dr/dc，用[-dr, dc]或[dr, -dc]来表示。[-dr, dc]因为是向上，对Right来说即是逆时针转90°，[dr, -dc]也就是顺时针转90°。

思考3：遍历完一边并改变遍历方向后，如何计算剩余的答案？

如果改变了方向，那么去掉第一行的矩阵，整个转移，咱们拿第一个case举例

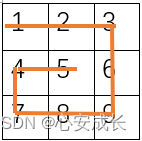
遍历完第一行后，变为

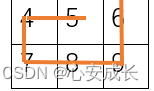
我们的递归方式，重新对矩阵进行处理，矩阵变换为

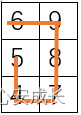
原始矩阵为m * n 新矩阵为n * (m - 1). 我们实际上不需要创建另外一个旋转矩阵，因为方向变化是由变量[dr, dc]处理的，到这里我们基本思路算是走完了。

代码实现步骤

定义函数 spiral(matrix, m, n, result, r, c, dr, dc)

1. matrix 是完整的矩阵输入。
2. m 和 n 是 matrix 的维度，在每次后续递归调用中从 m x n 更改为 n x (m - 1) 。
3. result 是正在完善最终结果数组。
4. r 和 c 表示我们当前所处的位置。最开始，我们将站在 [r, c] = [0, -1] 处，就在矩阵外部，面向 [0, 0] 。
5. dr 和 dc 表示遍历的方向。最初它将是 right = [dr, dc] = [0, 1] ，在每个后续递归调用中从 [dr, dc] 更改为 [dc, -dr] 。

public class spiralMatrix {
    private static void spiral(int[][] matrix, int nr, int nc, List<Integer> result, int r, int c, int dr, int dc) {
        if (nr == 0 || nc == 0) {
            return;
        }
        for (int i = 0; i < nc; i++) {
            r += dr; 
            c += dc;
            result.add(matrix[r][c]);
        }
        spiral(matrix, nc, nr - 1, result, r, c, dc, -dr);
    }

    public static List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> result = new ArrayList<>();
        spiral(matrix, matrix.length, matrix[0].length, result, 0, -1, 0, 1);
        return result;
    }
}

递归算法可以参考递归算法，你真的理解了吗？

递归的确有些复杂，慢慢理解，与君共勉。

曾经听说小明正在写一个递归算法，突然他停下来问自己：“我到底在做什么？”

隔壁老王回答：“你正在调用自己。”

小明说：“我知道，但是我为什么要这么做？”

老王回答：“因为你不知道如何不这样做。”