机器学习——线性模型
发布时间:2023年12月26日
【说明】文章内容来自《机器学习——基于sklearn》,用于学习记录。若有争议联系删除。
????????线性模型是在实践中广泛应用的一种模型,它利用输入特征的线性函数进行预测。
1、线性回归简介
????????在机器学习领域,常见的线性模型有线性回归、逻辑回归、岭回归等。其中,线性回归是利用数理统计中的回归分析来确定两种或两种以上变量相互依赖的定量关系的一种统计分析方法。线性回归有简单线性回归和多元线性回归两个主要类型。简单线性回归使用一个自变量通过拟合最佳线性关系来预测因变量的变化情况,因变量和自变量的关系用一条直线表示,其数学表达式如下:
其中,?是直线的斜率,b是截距。
![]()
1.1 线性回归实现
(1)绘制两个点的直线并输出直线方程。
#绘制经过两个点的直线并输出其方程
#两个点的坐标是(1,3)和(4,5)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
x = [[1],[4]]
y = [3,5]
lr = LinearRegression().fit(x,y)
z = np.linspace(0, 5, 20)
plt.scatter(x, y, s = 80)
plt.plot(z, lr.predict(z.reshape(-1, 1)), c = 'k')
plt.title('straight Line')
plt.show()
print('直线方程式:')
print('y = {:.3f}'.format(lr.coef_[0]), 'x', '+{:.3f}'.format(lr.intercept_))
#coef_o为回归系数(斜率),intercept_为截距【运行结果】
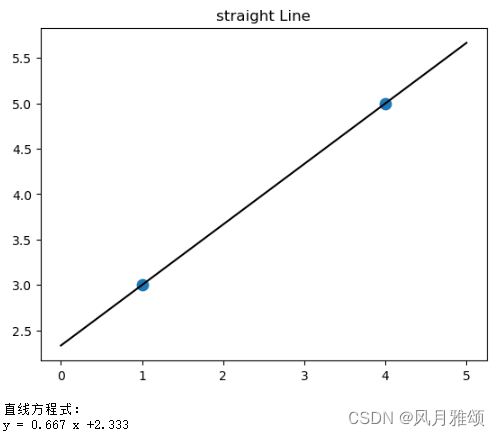
经过两个点的直线采用linear_model模块的LinearRegression 函数绘制,语法:
sklearn.linear_model.LinearRegression(fit_intercept = True)【参数说明】fit_intercept表示是否计算截距,默认为True。
(2)绘制三个点确定直线
#增加一个点(3,3)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
x = [[1],[4],[3]]
y = [3,5,3]
lr = LinearRegression().fit(x,y)
z = np.linspace(0, 5, 20)
plt.scatter(x, y, s = 80)
plt.plot(z, lr.predict(z.reshape(-1, 1)), c = 'k')
plt.title('straight Line')
plt.show()
print('直线方程式:')
print('y = {:.3f}'.format(lr.coef_[0]), 'x', '+{:.3f}'.format(lr.intercept_))【运行结果】

【结果分析】由于3个点不在一条直线上,故直线没有经过3个点中的任何一个点,而是与3个点的距离之和最小。
2、最小二乘法
????????最小二乘法(least square method)也称最小平方法,是回归分析中最简单、最经典的性模型,是基于均方误差最小化的模型求解方法。
最小二乘法的数学公式如下:
参数说明如下:
:第i个训练样本的真实值。
:第i个训练样本特征值组合预测函数。
2.1 线性回归用于披萨价格预测
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
x = [[6],[8],[10],[14],[18]]
y = [7,9,13,17.5,18]
lr = LinearRegression().fit(x, y)
z = np.linspace(-3, 20, 10)
plt.scatter(x, y, s = 50)
plt.plot(z, lr.predict(z.reshape(-1, 1)), c = 'k')
plt.axis([0, 20, 0, 20])
plt.xlabel('diameter')
plt.ylabel('money')
plt.grid(True)
plt.show()
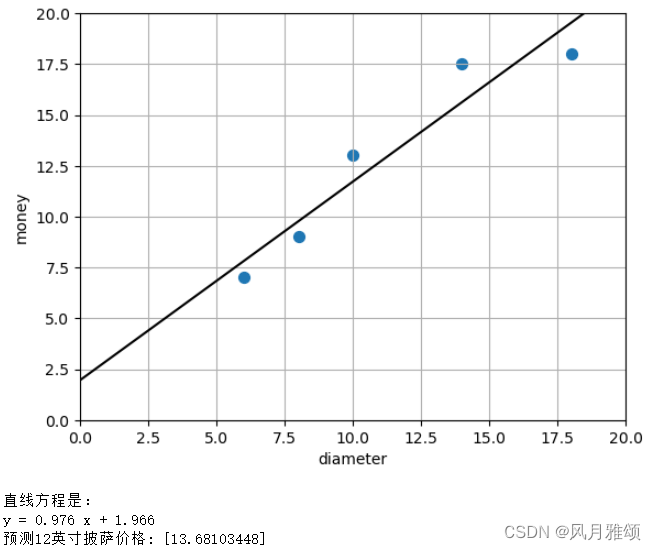
print('直线方程是:')
print('y = {:.3f}'.format(lr.coef_[0]), 'x', '+ {:.3f}'.format(lr.intercept_))
a = lr.predict([[12]])
print('预测12英寸披萨价格:',a)【运行结果】
3、逻辑回归
3.1 简介
????????逻辑回归(logistic regression)用于解决二分类问题,使用 Sigmoid函数(S形函数)进行分类,将连续实数值转化为0或1。Sigmoid函数的公式如下
单位阶跃函数与 Sigmoid函数如图所示。

linear_model 模块提供了LogisticRegression函数用于实现逻辑回归,语法如下:
model_LogisticRegression(penalty='l2', C=1.0)【参数说明】
- penalty:使用指定正则化项,默认为l2
- C:正则化力度。其值越小。损失函数越小,正则化强度越大,模型对损失函数惩罚越严重。
3.2 逻辑回归应用乳腺癌预测
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_breast_cancer
breast_cancer = load_breast_cancer()
print('特征:\n',breast_cancer.data.shape)
#划分数据集
x_train, x_test, y_train, y_test = train_test_split(breast_cancer.data, breast_cancer.target,
random_state = 33, test_size = 0.25)
#特征工程,标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
#逻辑回归预估器,重要参数为penalty 和 C
#max_iter 为梯度下降最大值
estimator = LogisticRegression(penalty = 'l2', solver = 'liblinear', C = 0.5, max_iter = 1000)
esimator = estimator.fit(x_train, y_train)
#coef_可以查看每个特征对应的参数
print('逻辑回归——权重系数为:\n', estimator.coef_)
print('逻辑回归——偏置为:\n',estimator.intercept_)
#模型评估
# 方法1:直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print(y_predict)
print('比对真实值和预测值:\n', y_test == y_predict)
#计算准确率
score = estimator.score(x_test, y_test)
print('准确率:\n',score)【运行结果】

文章来源:https://blog.csdn.net/qq_41566819/article/details/135219902
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- “Softechcl“app Tech Support(URL)
- 外包干了1个月,技术退步一大半。。。
- 优优嗨聚集团美团代运对外卖市场的影响与作用
- 利用cv2.rectangle和cv2.putText将标注框绘制到图片上,以便随时查看类别样子
- PC端微信公众号文章采集
- 双指针——移动零
- 相对布局RelativeLayout
- 关于 Redis 与传统关系型数据库的选择
- 快快销ShopMatrix 分销商城多端uniapp可编译5端 - 升级申请(可自定义申请表单)
- 从 Context 看 Go 设计模式:接口、封装和并发控制