自动控制原理——数学模型建立

目标

1.数学模型概念

描述系统输入、输出变量以及内部个变量之间的关系的数学表达式

2.建模方法

解析法（机理解析法）:

根据系统工作所依据的物理定律写运动方程

实验法（系统辨识法）：

给系统施加某种测试信号，记录输出响应，并用适当的数学模型去逼近系统的输入输出特性

（PID）看曲线调参就是这种？？？？

??

判断系统是否是线性时变系统：
是否线性看变量，是否时变看系数

结构图：（可用的数学关系）

?复数的概念

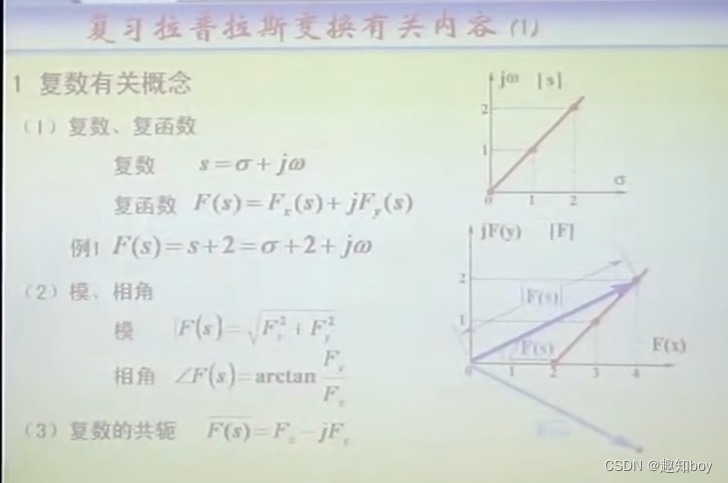
拉普拉斯变换

其中f(-1)是积分

现在主要是应用与（线性定常系统的分析

拉普拉斯反变换

相函数——部分分式

?

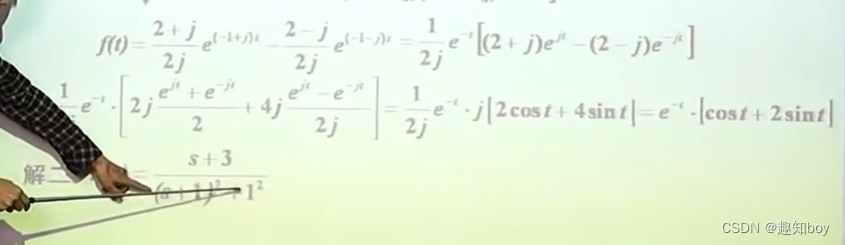
影响系统响应的因素

2.3.1 传递函数的定义

?

用尾一标准型，系统系数为增益? （此时为1）

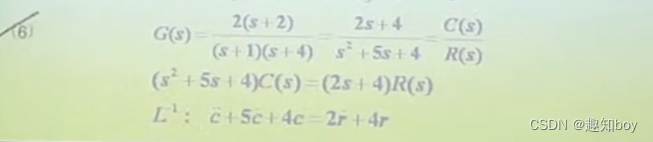
有初条件需要在L（s）到时域t后再用

初始条件引起的响应就是求时域时的齐次方程的解（忽略R（s ））

传递函数适用情况（零初始条件下、单输入单输出系统、线性定常系统）

梅逊增益公式

典型环节

闭环系统的开环传递函数？
就是输入的误差，输出的是反馈信号，这两个的关系

输入和扰动? 分别对应输出和误差

?

?