DropBlock

一、Dropout和DropBlock

在2D的数据中，dropout的效果并不好(图像具有空间局部依赖，在局部范围内，少量的像素特征值被drop掉，并不太影响整个模型的预测)

就是说，dropout只能随机的把多处的某一点神经元给丢掉，但是图像附近删除某一点，在其范围内，因为相似的比较多，在大范围看来，丢失的这一点对模型没什么影响，不会影响模型的预测，就像把一个小狗身上好多点，也不会影响别人知道他是一条小狗，DropBlock 不是随机地丢弃单个神经元，而是丢弃相邻的一整块神经元，就像一个小狗，可能把重要的一些一整块特征扔掉，就不太能认出来，如下图例子：

dropout的示例图：

DropBlock 示例图

DropBlock参考论文：
https://arxiv.org/abs/1810.12890

二、算法过程

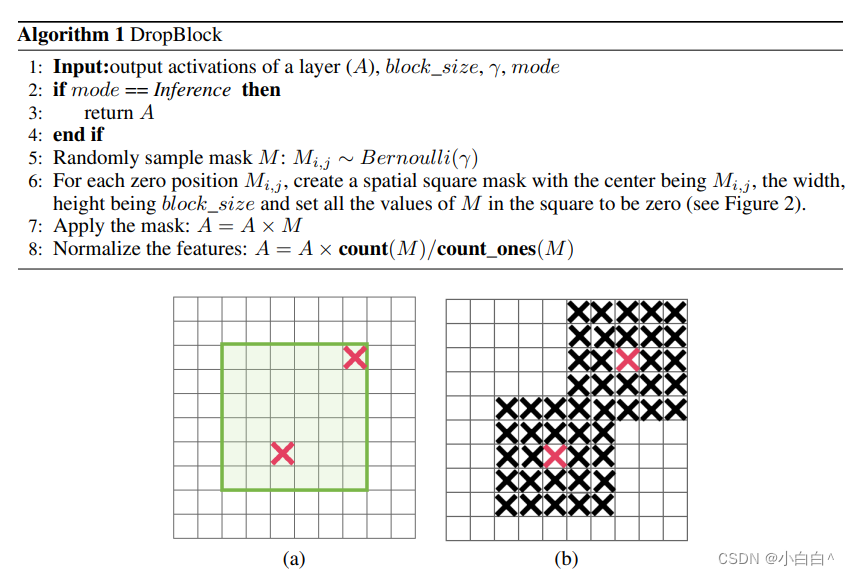
1 DropBlock 算法步骤解释

????????1.输入:

• • A: 神经网络层的输出激活值。
  • block_size: 决定丢弃块的大小。
  • γ (gamma): 控制每个特征图上将被丢弃的激活数量的参数。
  • mode: 指示当前是否为训练模式或推理模式。

????????2.模式判断:

• • 如果是推理模式，算法不会更改激活值，直接返回原始的 A。

????????3.随机采样遮罩 M:

• • 对于激活值矩阵 A 的每个元素，以 γ 作为概率进行伯努利随机采样，生成一个同样大小的遮罩矩阵 M。在 M 中，1表示保持激活值，0表示该位置的激活值将被丢弃。

????????4.生成丢弃块:

• • 对于遮罩 M 中的每个零值，围绕该点创建一个大小为 block_size 的正方形，将正方形内的所有值设置为零。这模拟了丢弃特征图上连续区域的过程。6

????????5.应用遮罩到激活值:

• • 将生成的遮罩 M 应用到激活值 A 上，通过逐元素乘法操作来丢弃相应的激活值。

????????6.特征标准化:

• • 最后，为了保持激活值的总量不变，使用比例因子 count(M)/count_ones(M) 对激活值 A 进行标准化。这里 count(M) 表示遮罩 M 中所有元素的数量，count_ones(M) 表示 M 中值为1的元素的数量。

2?γ（gamma）

在上述算法中，γ（gamma）的值是通过一个计算得到的，该计算考虑了希望丢弃的特征比例以及特征图的大小和Block的大小。γ 的计算确保了实际丢弃的激活值数量期望接近于预定义的丢弃率。

通常，γ 的计算涉及以下步骤：

1. 确定你希望在特征图上丢弃多少比例的激活值，即设定丢弃率 p。
2. 计算特征图的总激活值数目，即宽度 W 乘以高度 H。
3. 考虑到Block的大小，计算能够放置Block的起始点的数量。由于Block的边缘不能超出特征图的边界，因此能够放置Block的起始点的数量实际上少于特征图的总激活值数目。这通常通过 (H - block_size + 1) * (W - block_size + 1) 来计算。
4. 最后，γ 计算为希望的丢弃概率 p 除以能够放置Block的激活值数目，并乘以总激活值数目。

通过这种方式计算出的 γ，在每个激活值上应用伯努利分布进行采样，可以得到期望中大约有 p 比例的激活值被丢弃。这样的计算考虑到了Block的空间特性，使得在实际应用中，丢弃的激活值的比例与期望的丢弃率相匹配。

三、详细实现代码

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch import Tensor


class DropBlock2D(nn.Module):
    def __init__(self, p: float = 0.1, block_size: int = 7, inplace: bool = False):
        super(DropBlock2D, self).__init__()
        if p < 0 or p > 1:
            raise ValueError("DropBlock probability has to be between 0 and 1, "
                             "but got {}".format(p))
        if block_size < 1:
            raise ValueError("DropBlock block size必须大于0.")
        if block_size % 2 != 1:
            raise ValueError("当前代码实现的并不是特别完善，要求drop的区域大小必须是奇数")
        self.p = p
        self.inplace = inplace
        self.block_size = block_size

    # noinspection PyShadowingBuiltins
    def forward(self, input: Tensor) -> Tensor:
        if not self.training:
            return input

        N, C, H, W = input.size()
        mask_h = H - self.block_size + 1
        mask_w = W - self.block_size + 1
        gamma = (self.p * H * W) / ((self.block_size ** 2) * mask_h * mask_w)
        mask_shape = (N, C, mask_h, mask_w)
        # bernoulli:伯努利数据产生器，取值只有两种：0或者1；底层每个点会产生一个随机数，随机数小于等于gamma的，对应位置就是1；否则就是0
        mask = torch.bernoulli(torch.full(mask_shape, gamma, device=input.device))
        # 在 mask 的四个边界上添加填充。这里 [self.block_size // 2] * 4 产生了一个长度为4的列表，
        # 每个元素都是 self.block_size // 2 的值。在 PyTorch 的 F.pad 中，
        # 这个列表定义了填充的大小，格式为 [左, 右, 上, 下]
        mask = F.pad(mask, [self.block_size // 2] * 4, value=0)  # 当前0表示保留，1表示删除
        mask = F.max_pool2d(mask, (self.block_size, self.block_size), (1, 1), self.block_size // 2)

        mask = 1.0 - mask  # 最终的drop mask产生了， 0删除，1保留

        # .numel() 方法用于返回一个张量（Tensor）中元素的总数
        normalize_scale = mask.numel() / (1e-6 + mask.sum())  # 为了保证训练和推理的数据一致性

        if self.inplace:
            input.mul_(mask * normalize_scale)
        else:
            input = input * mask * normalize_scale
        return input