洛谷 P1364 医院设置

题目描述

设有一棵二叉树，如图：

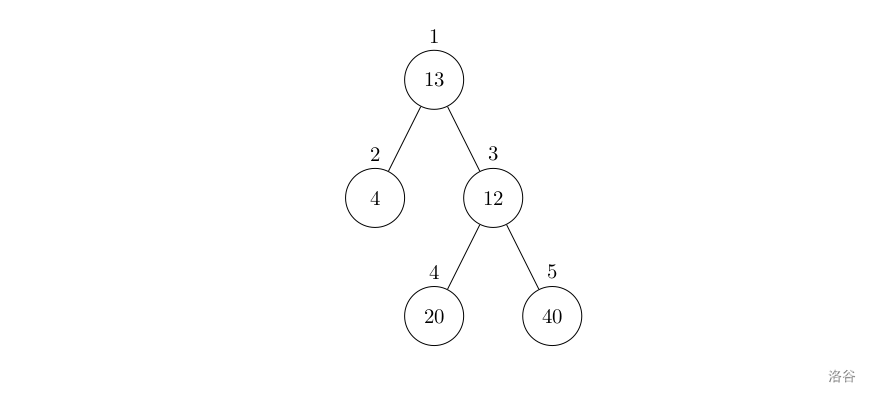
其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为?11。如上图中，若医院建在?11?处，则距离和?=4+12+2×20+2×40=136；若医院建在?3?处，则距离和=4×2+13+20+40=81。

输入格式

第一行一个整数?n，表示树的结点数。

接下来的?n?行每行描述了一个结点的状况，包含三个整数 w,u,v，其中?w?为居民人口数，u?为左链接（为?0?表示无链接），v?为右链接（为0?表示无链接）。

输出格式

一个整数，表示最小距离和。

输入输出样例

输入 #1

5						
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0

输出 #1

81

说明/提示

数据规模与约定

对于?100%的数据，保证 1≤n≤100，0≤u,v≤n，1≤w≤10^5。

?解题思路

本题求距离和最短，可以用广搜，首先一重循环遍历以不同点为终点，再嵌套一重循环，遍历每一个起点，求所以起点到终点的距离之和，每次更新最小值，我们知道二叉树的每个结点有三个去向父节点，左孩子，右孩子，题目已经要求输入每个点的左右孩子，所以只要求出每个点的父节点就行了，具体操作看代码。

#include<stdio.h>
struct nb {//2叉树结点
	int data;//每个结点的人数
	int f;//父节点
	int lchild, rchild;//左右孩子
}a[110];
struct nm {//列队用于广搜
	int x;//编号
	int s;//步数
}b[100100];
int n, book[110];//book数组用于标记 
void dfs(int x,int y)//求父节点 x为编号，y为父节点
{
	if (x == 0)//没有孩子，结束递归
		return;
	a[x].f = y;
	dfs(a[x].lchild, x);//往左孩子走
	dfs(a[x].rchild, x);//往右孩子走
	return;
}
int main()
{
	int i, j, min = 1e9;
	scanf("%d", &n);
	for(i=1;i<=n;i++)//
		scanf("%d %d %d", &a[i].data, &a[i].lchild, &a[i].rchild);
	dfs(1, 0);//从根结点开始
	for (i = 1; i <= n; i++)//分别以每一个点为终点
	{
		int sum = 0;
		for (j = 1; j <= n; j++)//遍历每一个起点
		{
			if (i == j)//起点终点重合直接跳过
				continue;
			for (int q = 1; q <= n; q++)//初始化标记数组
				book[q] = 0;
			//列队插入起点
			int hard = 1, tail = 1, flag = 0;
			b[tail].x = j; b[tail].s = 0;
			book[j] = 1; tail++;
			while (hard < tail)
			{
				for (int q = 1; q <= 3; q++)//往三个方向走，父节点，左孩子，右孩子
				{
					int t;
					if (q == 1)
						t = a[b[hard].x].f;//往父节点走
					else if (q == 2)
						t = a[b[hard].x].lchild;//往左孩子
					else
						t = a[b[hard].x].rchild;//往右孩子
					if (t == 0)//没有子节点或父节点
						continue;
					if (book[t] == 0)//如果第一次来这个点
					{
						//入队操作
						b[tail].x = t; book[t] = 1;
						b[tail].s = b[hard].s + 1; tail++;
						if (t == i)//如果找到终点
						{
							flag = 1;
							break;
						}
					}
				}
				if (flag == 1)
				{
					sum += a[j].data * b[tail - 1].s;//计算路程
					break;
				}
				hard++;
			}
		}
		if (min > sum)//更新最小值
			min = sum;
	}
	printf("%d", min);//打印结果
	return 0;
}