排序算法之七:归并排序(非递归)
发布时间:2024年01月15日
1.非递归实现思路
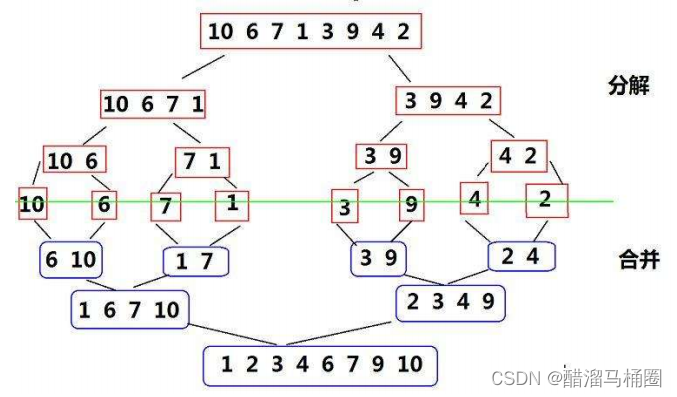
我们之前学习了递归实现的归并排序,是分治的思想,即先分解,再归并
这篇文章我们讲一下非递归的实现
非递归实现的思路是模拟递归的过程,在递归过程中,我们找key将数组分成左右数组,然后递归子数组,知道该数组剩一个元素,然后归并:两个两元素数组归并为四元素数组,两个四元素数字归并为八元素数组
而非递归的实现不需要递归子数组进行分解,我们可以将n个元素的数组看作n个数组,直接进行下面的合并

我们先设gap为1,表示先控制一个元素的数组进行归并,malloc一个临时数组tmp,归并到tmp数组;一整趟归并结束后gap*=2,同时将归并完成的数组拷贝到原数组,继续控制两元素的数组进行归并,直到gap>=n则停止归并,此时原数组已经有序了
2.图示归并
归并的过程和递归方式的归并排序一样
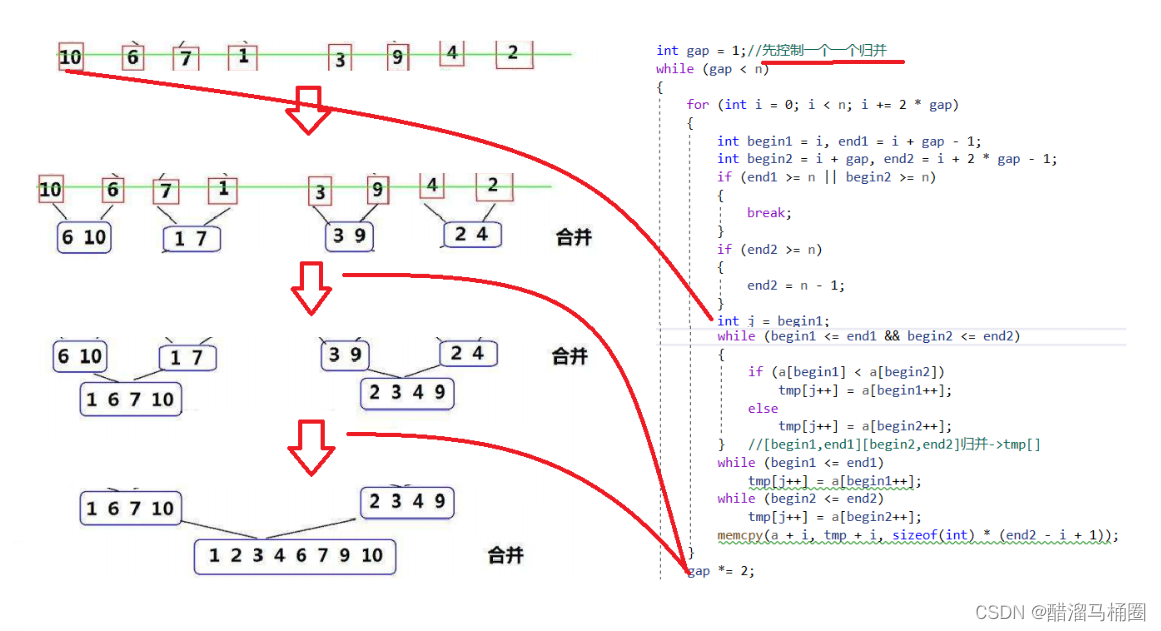
每次归并的时候,两个数组中找小的排到前面,排空一个数组之后将另外一个数组尾插到后面即可
3.代码展示
函数代码和测试代码如下
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail!");
return;
}
int gap = 1;//先控制一个一个归并
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
if (end1 >= n || begin2 >= n)
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}
int j = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
tmp[j++] = a[begin1++];
else
tmp[j++] = a[begin2++];
} //[begin1,end1][begin2,end2]归并->tmp[]
while (begin1 <= end1)
tmp[j++] = a[begin1++];
while (begin2 <= end2)
tmp[j++] = a[begin2++];
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
gap *= 2;
}
free(tmp);
}
int main()
{
int i = 0;
int a[] = { 10,10,2,5,7,9,3,4,5,4,1,0 };
int n = sizeof(a) / sizeof(a[0]);
for (i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
MergeSortNonR(a, n);
for (i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
return 0;
}
文章来源:https://blog.csdn.net/m0_74722801/article/details/135609511
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!