单相电压二重化逆变电路的仿真

所谓多重化就是用几个逆变器，使它们输出相同频率的矩形波在相位上移开一定的角度进行叠加，以减小谐波，从而获得接近正弦的阶梯波形。电压型逆变器和电流型逆变器都可以实现多重化。

在Simulink中搭建单相电压二重化逆变电路

二重单相电压型逆变电路由两个单相全桥逆变电路组成，二者输出通过变压器串联起来，两个单相逆变电路的输出都是矩形波，其中包含所有的奇次谐波。把两个单相逆变器导通的相位错开φ=60°，则对于两个单项逆变器输出电压中的3次谐波来说，它们就错开了3×60°=180°，通过变压器串联合成后，两者中所含3次谐波相互抵消，所得到的总输出电压中就不含3次谐波。

所搭建的三相桥式整流电路仿真模型如下图所示。

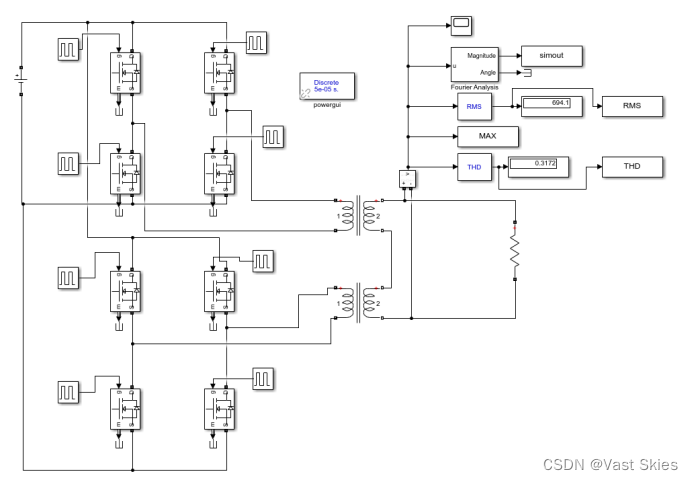
从仿真模型可知，它由主电路和控制电路组成，主电路是两个单相桥，使用4个MOSFET构成。控制电路由脉冲触发器构成。

先加入直流电源（DC Voltage Source），设置电压值为400。加入变压器模块（Linear Transformer），把频率改为50Hz，并且把Three windings transformer ?前面的复选框中的“√”去掉，成为两绕组的变压器。

给每一个MOSFET接入一个脉冲触发器，统一设置参数为：峰值为1，周期T为0.02s，脉冲宽度为50。给上面一组设置相位延迟时间分别为：0s，0.02/360*(a)，0.02/360*(180)，0.02/360*(a+180)，a就是需要改变的参数，即内部移相角θ。给下面一组设置相位延迟时间分别为：0.02/360*30，0.02/360*(30+a)，0.02/360*(30+180)，0.02/360*(30+180+a)，30就是加上的变流器之间的外移相角φ=30°，a就是需要改变的参数，即内部移相角θ。

连接完整电路，加上R=8Ω的电阻负载，设置好电流与电压的测量环节，加入傅里叶分解模块，设置Harmonic numbers为[1 3 5 6 7 9]。随后即可开始单次仿真。

在MATLAB中编写代码实现改变参数的多次循环仿真

代码编写

clear;clc;

%% 循环遍历

n=180;
results = zeros(n+1, 8);

for a=0:n
sim('Ti_Mu_1_Mo_Xing');
b=a+1;
results(b, 1) = max(MAX); % 幅值
results(b, 2) = RMS(end); % 有效值
results(b, 3) = THD(end); % 畸变率
results(b, 4) = simout(end,2)/simout(end,1); % 3次谐波含量
results(b, 5) = simout(end,3)/simout(end,1); % 5次谐波含量
results(b, 6) = simout(end,4)/simout(end,1); % 6次谐波含量
results(b, 7) = simout(end,5)/simout(end,1); % 7次谐波含量
results(b, 8) = simout(end,6)/simout(end,1); % 9次谐波含量
end
save Ti_Mu_1_Shu_Jv.mat results

代码说明

在这样执行之后，即可产生从0度到180的各项数据，包括输出电压幅值、有效值、输出电压畸变率，3、5、6、7、9次谐波含量。

最后，保存至一个数据文件以便绘图使用。

仿真结果说明

单个逆变器的时序波形及输入输出电压关系

内部移相角θ为180°时

输出电压的波形图如下。

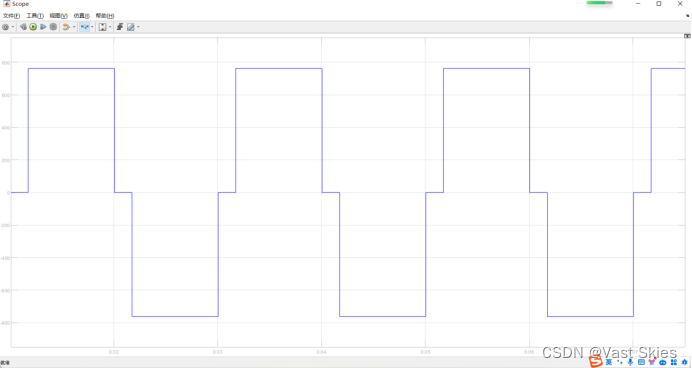
内部移相角θ为60°时

输出电压的波形图如下。

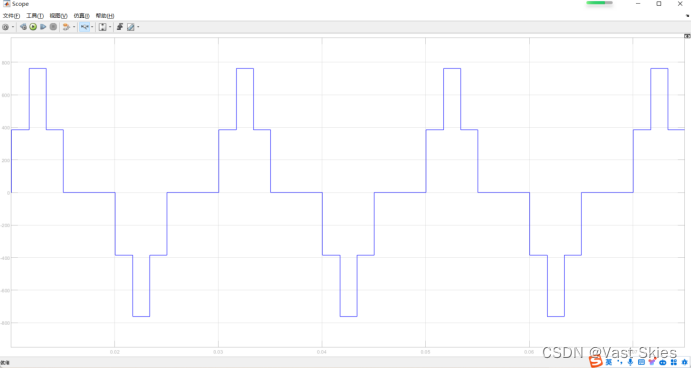
内部移相角θ为30°时

输出电压的波形图如下。

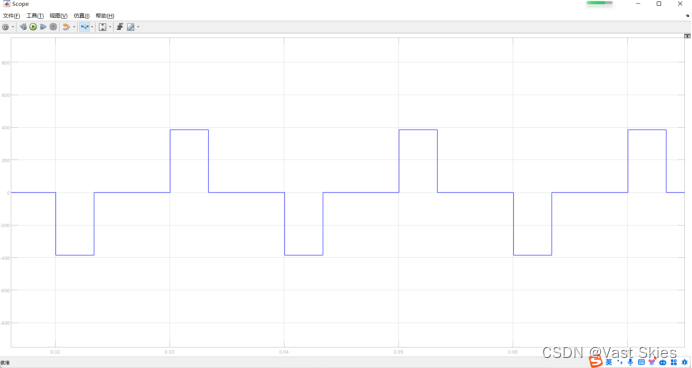
输出电压幅值、有效值、输出电压畸变率，3、5、6、7、9次谐波含量与相位角的关系

根据刚才循环得到的数据即可绘制这些关系图。

代码编写

%% 绘制图像
load Ti_Mu_1_Shu_Jv.mat
figure
subplot(1,3,1)
plot(0:180,results(1:end, 1)')
xlabel('内部移相角θ')
ylabel('幅值/V')

subplot(1,3,2)
plot(0:180,results(1:end, 2)')
xlabel('内部移相角θ')
ylabel('有效值/V')

subplot(1,3,3)
plot(1:180,results(2:end, 3)')
xlabel('内部移相角θ')
ylabel('畸变率')

figure
title("谐波含量")
subplot(2,3,1)
plot(1:180,results(2:end, 4)')
xlabel('内部移相角θ')
ylabel('3次谐波含量')

subplot(2,3,2)
plot(1:180,results(2:end, 5)')
xlabel('内部移相角θ')
ylabel('5次谐波含量')

subplot(2,3,3)
plot(1:180,results(2:end, 6)')
ylim([-0 0.5])
xlabel('内部移相角θ')
ylabel('6次谐波含量')

subplot(2,3,4)
plot(1:180,results(2:end, 7)')
xlabel('内部移相角θ')
ylabel('7次谐波含量')

subplot(2,3,5)
plot(1:180,results(2:end, 8)')
xlabel('内部移相角θ')
ylabel('9次谐波含量')

结果说明

通过绘图，我们得到这些量和内部移相角θ的关系。

首先得到相位角与输出电压幅值、有效值、输出电压畸变率的关系。

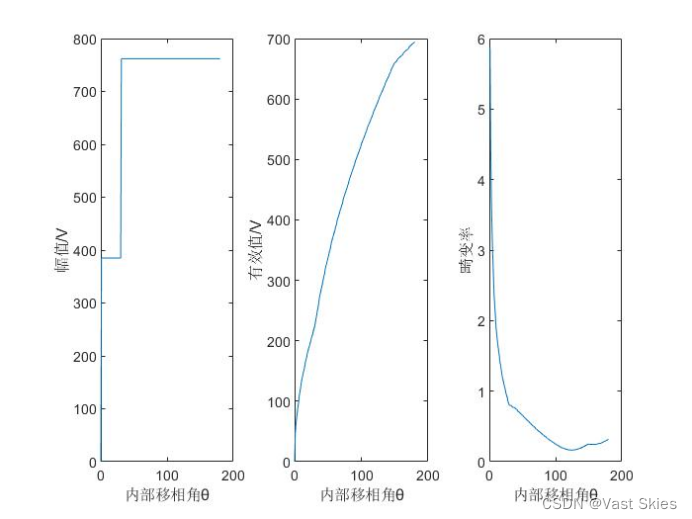
随后可以得到3、5、6、7、9次谐波含量与相位角的关系。

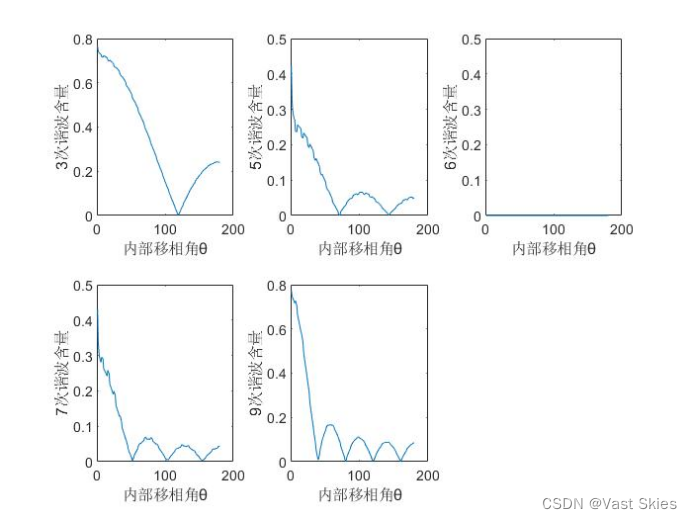
其中，6次谐波在所有角度情况下都是不包含的。