MATLAB - 比较 DDPG Agent 和 LQR 控制器

发布时间：2024年01月19日

系列文章目录

前言

本示例展示了如何训练深度确定性策略梯度（DDPG）Agent，以控制 MATLAB? 中建模的二阶线性动态系统。该示例还将 DDPG Agent 与 LQR 控制器进行了比较。

有关 DDPG 代理的更多信息，请参阅深度确定性策略梯度 (DDPG) 代理。有关如何在 Simulink? 中训练 DDPG agent 的示例，请参阅训练 DDPG agent 向上摆动并平衡摆锤。

一、双积分器 MATLAB 环境

本例的强化学习环境是一个具有增益的二阶双积分器系统。训练目标是通过施加力输入来控制二阶系统中质量的位置。

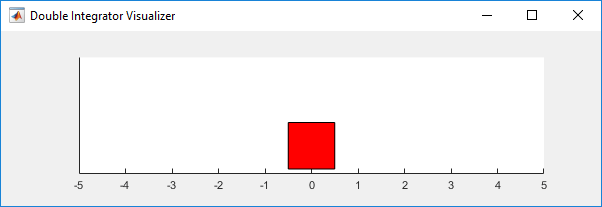
对于这种环境：

质量从-4 或 4 个单位的初始位置开始。
从环境中观测到的是质量的位置和速度。
如果质量从初始位置移动超过 5 米，或者∣x∣<0.01，则事件结束。
每个时间步提供的奖励 $r_t$ 是 r(t) 的离散化： $r(t)=-(x(t)^{'}Qx(t)+u(t)^{'}Ru(t))$

这里

x 是质量的状态矢量。
u 是施加在质量上的力。
Q 是控制性能的权重矩阵；Q=[10 0;0 1]。
R 是控制力度的权重；R=0.01。

有关该模型的更多信息，请参阅负载预定义控制系统环境。

在本例中，环境是一个线性动态系统，环境状态可直接观测，奖励是观测和行动的二次函数。因此，寻找使长期累积奖励最小化的行动序列问题是一个离散时间线性 - 二次方最优控制问题，已知最优行动是系统状态的线性函数。这个问题也可以使用线性 - 二次方调节器（LQR）设计来解决，在示例的最后部分，您可以将 Agent 与 LQR 控制器进行比较。

二、创建环境界面

为双积分系统创建预定义的环境界面。?

env = rlPredefinedEnv("DoubleIntegrator-Continuous")

env = 
  DoubleIntegratorContinuousAction with properties:

             Gain: 1
               Ts: 0.1000
      MaxDistance: 5
    GoalThreshold: 0.0100
                Q: [2x2 double]
                R: 0.0100
         MaxForce: Inf
            State: [2x1 double]

界面上有一个连续的动作空间，Agent 可以对质量施加从-Inf 到 Inf 的力值。采样时间存储在 env.Ts，连续时间成本函数矩阵分别存储在 env.Q 和 env.R。

从环境界面获取观察和行动信息。

obsInfo = getObservationInfo(env)

obsInfo = 
  rlNumericSpec with properties:

     LowerLimit: -Inf
     UpperLimit: Inf
           Name: "states"
    Description: "x, dx"
      Dimension: [2 1]
       DataType: "double"

actInfo = getActionInfo(env)

actInfo = 
  rlNumericSpec with properties:

     LowerLimit: -Inf
     UpperLimit: Inf
           Name: "force"
    Description: [0x0 string]
      Dimension: [1 1]
       DataType: "double"

重置环境并获取其初始状态。

x0 = reset(env)

修复随机发生器种子，实现可重复性。

rng(0)

三、创建 DDPG Agent

DDPG Agent 使用 Q 值函数批判器逼近折现的长期累积奖励。Q 值函数批判器必须接受一个观察结果和一个行动作为输入，并返回一个标量（估计的折现长期累积奖励）作为输出。要在批判器中近似地计算 Q 值函数，可以使用神经网络。已知最优策略的价值函数是二次函数，因此使用一个包含二次层（如 quadraticLayer 所述，输出二次单项式向量）和全连接层（提供输入的线性组合）的网络。

将每个网络路径定义为层对象数组，并从环境规范对象中获取观察空间和动作空间的维度。为网络输入层指定名称，这样就可以将它们连接到输出路径，之后再将它们与相应的环境通道明确关联。由于不需要偏置项，请将偏置项设置为零（Bias=0）并防止其发生变化（BiasLearnRateFactor=0）。

有关创建值函数近似值的更多信息，请参阅创建策略和值函数。

% Observation and action paths
obsPath = featureInputLayer(obsInfo.Dimension(1),Name="obsIn");
actPath = featureInputLayer(actInfo.Dimension(1),Name="actIn");

% Common path
commonPath = [
    concatenationLayer(1,2,Name="concat")
    quadraticLayer
    fullyConnectedLayer(1,Name="value", ...
        BiasLearnRateFactor=0,Bias=0)
    ];

% Add layers to layerGraph object
criticNet = layerGraph(obsPath);
criticNet = addLayers(criticNet,actPath);
criticNet = addLayers(criticNet,commonPath);

% Connect layers
criticNet = connectLayers(criticNet,"obsIn","concat/in1");
criticNet = connectLayers(criticNet,"actIn","concat/in2");

查看评论家网络配置。

figure
plot(criticNet)

转换为 dlnetwork 并显示权重数。?

criticNet = dlnetwork(criticNet);
summary(criticNet)

   Initialized: true

   Number of learnables: 7

   Inputs:
      1   'obsIn'   2 features
      2   'actIn'   1 features

使用 criticNet、环境观测和动作规范以及分别与环境观测和动作通道连接的网络输入层名称创建评论家近似器对象。更多信息，请参阅 rlQValueFunction。

critic = rlQValueFunction(criticNet, ...
    obsInfo,actInfo, ...
    ObservationInputNames="obsIn",ActionInputNames="actIn");

用随机观察和行动输入来检查评论家。

getValue(critic,{rand(obsInfo.Dimension)},{rand(actInfo.Dimension)})

ans = single
    -0.3977

DDPG agent 使用参数化的连续确定性策略，该策略由连续确定性行动者学习。该行为体必须接受一个观察结果作为输入，并返回一个行动作为输出。要在行为体内部逼近策略函数，可以使用神经网络。在本例中，已知最优策略与状态呈线性关系，因此使用一个具有全连接层的浅层网络来提供两个网络输入的线性组合。

将网络定义为层对象数组，并从环境规范对象中获取观察空间和行动空间的维度。由于不需要偏置项，就像对评论家所做的那样，将偏置项设为零（Bias=0）并防止其改变（BiasLearnRateFactor=0）。有关行为体的更多信息，请参阅创建策略和价值函数。

actorNet = [
    featureInputLayer(obsInfo.Dimension(1))
    fullyConnectedLayer(actInfo.Dimension(1), ...
        BiasLearnRateFactor=0,Bias=0)
    ];

转换为 dlnetwork 并显示权重数。

actorNet = dlnetwork(actorNet);
summary(actorNet)

   Initialized: true

   Number of learnables: 3

   Inputs:
      1   'input'   2 features

使用 actorNet 以及观察和动作规范创建演员。更多信息，请参阅 rlContinuousDeterministicActor。

actor = rlContinuousDeterministicActor(actorNet,obsInfo,actInfo);

用随机观测输入检查演员。

getAction(actor,{rand(obsInfo.Dimension)})

ans = 1x1 cell array
    {[0.3493]}

使用演员和评论家创建 DDPG Agent。更多信息，请参阅 rlDDPGAgent。

agent = rlDDPGAgent(actor,critic);

使用点符号指定 Agent 的选项，包括评论家的训练选项。或者，也可以在创建 Agent 之前使用 rlDDPGAgentOptions 和 rlOptimizerOptions 对象。

agent.AgentOptions.SampleTime = env.Ts;
agent.AgentOptions.ExperienceBufferLength = 1e6;
agent.AgentOptions.MiniBatchSize = 32;
agent.AgentOptions.NoiseOptions.StandardDeviation = 0.3;
agent.AgentOptions.NoiseOptions.StandardDeviationDecayRate = 1e-7;
agent.AgentOptions.ActorOptimizerOptions.LearnRate = 1e-4;
agent.AgentOptions.ActorOptimizerOptions.GradientThreshold = 1;
agent.AgentOptions.CriticOptimizerOptions.LearnRate = 5e-3;
agent.AgentOptions.CriticOptimizerOptions.GradientThreshold = 1;

四、初始化 Agent 参数

演员执行的策略是 $u=K_1x_1+K_2x_2=Kx$ ，其中反馈增益 K 1 和 K 2 是演员网络的两个权重。可以看出，如果这些增益为负值，闭环系统就会稳定，因此，将它们初始化为负值可以加快收敛速度。

Q 值函数的结构如下：

$Q(x,u)=W_1x_1^2+W_2x_1x_2+W_3x_2^2+W_4x_1u+W_5x_2u+W_6u^2$

其中 W i 是全连接层的权重。或者，以矩阵形式表示

$Q(x,u)=\begin{bmatrix}x_1&x_2&u\end{bmatrix}\begin{bmatrix}W_1&\frac{W_2}{2}&\frac{W_4}{2}\\W_2&W_3&\frac{W5}{2}\\\frac{W_4}{2}&\frac{W5}{2}&W6\end{bmatrix}\begin{bmatrix}x_1\\x_2\\u\end{bmatrix}=\begin{bmatrix}x^T&u\end{bmatrix}W\begin{bmatrix}x\\u\end{bmatrix}$

对于固定的 u=Kx 政策，长期累积奖励（即政策的价值）变为

$V(x)=Q(x,Kx)=\\\\x^T\begin{bmatrix}I&K^T\end{bmatrix}W\begin{bmatrix}I\\K\end{bmatrix}x=\\\\x^TPx$

由于奖励总是负值，要正确近似累积奖励，P 和 W 必须都是负定值。因此，为了加快收敛速度，应初始化评论家网络权重 Wi，使 W 为负定值。

% Create diagonal matrix with negative eigenvalues
W = -single(diag([1 1 1])+0.1)

W = 3x3 single matrix

   -1.1000   -0.1000   -0.1000
   -0.1000   -1.1000   -0.1000
   -0.1000   -0.1000   -1.1000

% Extract indexes of upper triangular part of a 3 by 3 matrix
idx = triu(true(3))

idx = 3x3 logical array

   1   1   1
   0   1   1
   0   0   1

% Update parameters in the actor and critic
par = getLearnableParameters(agent);
par.Actor{1} = -single([1 1]);
par.Critic{1} = W(idx)';
setLearnableParameters(agent,par);

用随机观测输入检查 Agent。

getAction(agent,{rand(obsInfo.Dimension)})

ans = 1x1 cell array
    {[-1.2857]}

五、训练 Agent

要训练 Agent，首先要指定训练选项。本例中使用以下选项。

在训练会话中最多运行 5000 个集，每个集最多持续 200 个时间步。
在剧集管理器对话框中显示训练进度（设置 Plots 选项），并禁用命令行显示（Verbose 选项）。
当 Agent 获得的移动平均累积奖励大于-66 时，停止训练。此时，Agent 可以用最小的控制力控制质量的位置。

更多信息，请参阅 rlTrainingOptions。

trainOpts = rlTrainingOptions(...
    MaxEpisodes=5000, ...
    MaxStepsPerEpisode=200, ...
    Verbose=false, ...
    Plots="training-progress",...
    StopTrainingCriteria="AverageReward",...
    StopTrainingValue=-66);

在训练或模拟过程中，您可以使用绘图功能将双积分器环境可视化。

plot(env)

使用 train 训练 Agent。训练这个 Agent 是一个计算密集型过程，需要几个小时才能完成。为节省运行此示例的时间，请将 doTraining 设为 false，以加载一个预训练过的 Agent。要自己训练 Agent，请将 doTraining 设为 true。

doTraining = false;
if doTraining
    % Train the agent.
    trainingStats = train(agent,env,trainOpts);
else
    % Load the pretrained agent for the example.
    load("DoubleIntegDDPG.mat","agent");
end

六、仿真 DDPG Agent

要验证训练有素的 Agent 的性能，请在双积分器环境中对其进行模拟。有关代理模拟的更多信息，请参阅 rlSimulationOptions 和 sim。?

simOptions = rlSimulationOptions(MaxSteps=500);
experience = sim(env,agent,simOptions);

totalReward = sum(experience.Reward)

totalReward = -65.9875

七、求解 LQR 问题

函数 lqrd（控制系统工具箱）用于解决离散 LQR 问题，如本示例中的问题。该函数计算最佳离散时间增益矩阵 Klqr 以及 Riccati 方程 Plqr 的解。当 Klqr 通过状态负反馈连接到被控对象输入（力）时，env.Q 和 env.R 所指定的离散时间等效成本函数就会向前最小化。此外，从初始状态 x0 开始，从初始时间到无穷大的累积成本等于 x0'*Plqr*x0 。

使用 lqrd 求解离散 LQR 问题。

[Klqr,Plqr] = lqrd([0 1;0 0],[0;env.Gain],env.Q,env.R,env.Ts);

这里，[0 1;0 0] 和 [0;env.Gain] 分别是双积分器系统的连续时间转换矩阵和输入增益矩阵。

如果未安装 Control System Toolbox?，请使用默认示例值的解决方案。

Klqr = [17.8756 8.2283]；
Plqr = [4.1031 0.3376; 0.3376 0.1351]；
如果演员策略 u=Kx 成功逼近了最优策略，那么得到的 Km 必须接近 -Klqr（负号是因为 Klqr 是假设负反馈连接计算的）。

如果评论家学习到了最优价值函数的良好近似值，那么结果 P（如前所述）必须接近-Plqr（负号是由于奖励被定义为成本的负值）。

八、将 DDPG Agent 与最优控制器进行比较

提取 Agent 内演员和评论家的参数（权重）。

par = getLearnableParameters(agent);

显示演员权重。

K = par.Actor{1}

K = 1x2 single row vector

  -15.4601   -7.2076

请注意，这些增益与最优解 -Klqr 的增益接近：

-Klqr

ans = 1×2

  -17.8756   -8.2283

重新创建分别定义 Q 值和价值函数的矩阵 W 和 P。首先，将 W 重新初始化为零。

W = zeros(3);

?将评论家权重放在 Wc 的上三角部分。

W(idx) = par.Critic{1};

创建 W c 如前定义。

W = (W + W')/2

W = 3×3

   -4.9869   -0.7788   -0.0548
   -0.7788   -0.3351   -0.0222
   -0.0548   -0.0222    0.0008

利用 W 和 K，按照前面的定义计算 P。

P = [eye(2) K']*W*[eye(2);K]

P = 2x2 single matrix

   -3.1113    0.0436
    0.0436    0.0241

注意，增益接近里卡提方程 -Plqr 的解。

-Plqr

ans = 2×2

   -4.1031   -0.3376
   -0.3376   -0.1351

获取环境初始状态。

x0=reset(env);

?价值函数是在使用演员制定的政策时，对未来累积长期回报的估计。根据评论家权重计算初始状态下的价值函数。这就是训练窗口中显示的与第 Q0 集相同的值。

q0 = x0'*P*x0

q0 = single
    -49.7803

请注意，该值与验证模拟中获得的实际奖励 totalReward 很接近，这表明评论家学习到了演员所制定策略的价值函数的良好近似值。

按照 LQR 控制器制定的真正最优策略，计算初始状态的值。

-x0'*Plqr*x0

ans = -65.6494

这个值也非常接近验证模拟中得到的值，证实演员学习并执行的策略是真正最优策略的良好近似值。

文章来源:https://blog.csdn.net/weixin_46300916/article/details/135638527
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！