流水车间调度问题（Flow Shop Scheduling Problem）

目录

1.问题描述

2.问题假设

3.混合整数规划模型

3.1符号定义

3.2目标函数

3.3约束条件

4.基于遗传算法的流水车间调度问题求解

4.1算法设计

4.1.1染色体编码

4.1.2生成初始种群

（1）CDS方法

（2）Dannenbring的方法

①RA算法

②RACS和RAES算法

4.1.3适应度函数

4.1.3选择操作

4.1.4交叉操作

4.1.5变异操作

4.1.6终止条件

4.2.算例及仿真

4.2.1算例

4.2.2遗传算法运行参数

4.2.3求解结果

5.代码（Python）

5.1Gurobi求解FSP

5.2遗传算法（GA）求解FSP

参考文献

---

1.问题描述

? ? ? ?流水车问调度问题一般可以描述为n个工件要在m台机器上加工，每个工件需要经过m道工序，每道工序要求不同的机器，n个工件在m台机器上的加工顺序相同。工件在机器上的加工时间是给定的，设为tij(i=1,…,n;j=1,…,m)。问题的目标是确定n个工件在每台机器上的最优加工顺序，使所要求的生产指标达到最优。采用常规的调度三分法表示为Fm|prmu|Cmax。其中:Fm表示为m台机器的流水车间调度;prmu表明所有工作经过每一台机器的加工顺序是一致的;Cmax表示为工件的最大完工时间。

2.问题假设

????????（1）每个工件在机器上的加工顺序是给定的；

????????（2）一台机器不能同时加工多个工件；

????????（3）一个工件不能同时由多台机器加工；

????????（4）工序不能预定；

????????（5）工序的准备时间与顺序无关，且包含在加工时间中或者可以忽略不计；

????????（6）工件在每台机器上的加工顺序相同，且是确定的。

3.混合整数规划模型

3.1符号定义

3.2目标函数

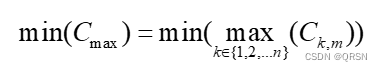
3.3约束条件

????????约束条件式（1）和（2）表示在排列π中各工件出现并且只能出现一次。

????????约束条件式（3）表示在第一台机器上加工的第一个工件的完成时间。

????????约束条件式（4）表示一台机器在同一时刻只能加工一个工件。

????????约束条件式（5）表示一个工件不能同时由多台机器加工。

????????约束条件（6）表示所有工序的完成时间均大于零。

????????约束条件式（7）表示0-1约束变量。

4.基于遗传算法的流水车间调度问题求解

4.1算法设计

4.1.1染色体编码

????????自然数编码。

4.1.2生成初始种群

????????前m-1个个体由CDS方法生成，1个个体由Dannenbring的方法生成，剩下的个体由交换变异算子生成，交换变异算子将随机选择一个个体并在该个体上随机选择两个片段进行交换以产生新的个体，重复该操作直至达到设定的种群规模，种群规模为60。

（1）CDS方法

（2）Dannenbring的方法

①RA算法

②RACS和RAES算法

4.1.3适应度函数

????????目标函数是最小化 最大加工时间。

????????适应度函数如下：

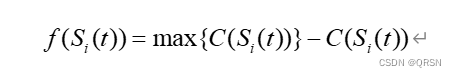
????????Si(t)表示第t代第i个个体，C(Si(t))表示第t代第i个个体的最大完工时间，f(Si(t))表示第t代第i个个体的适应度函数值。

4.1.3选择操作

????????采用比例选择算子，最大完工时间越短的个体被选中的可能性越高。

4.1.4交叉操作

????????采用线性次序交叉操作（LOX）。

4.1.5变异操作

????????采用移位变异操作。

4.1.6终止条件

????????迭代100代。

4.2.算例及仿真

4.2.1算例

????????每个工件在每台机器上的处理时间是从1到20的均匀分布中随机抽样来确定。

????????n的取值有8，10，15，20，30。

????????m的的取值有5，10，15，20。

4.2.2遗传算法运行参数

4.2.3求解结果

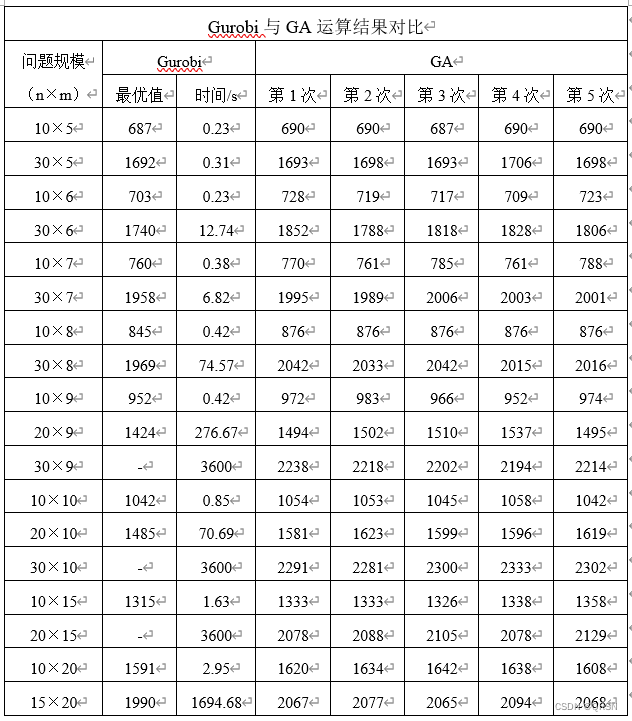
5.代码（Python）

5.1Gurobi求解FSP

from gurobipy import *
import numpy as np
import time

# 参数设定
sequence=[] # 加工的次序
n = 20 # 工件总数
m = 10 # 机器总数
low = 1 # 加工时间最小值
high = 99 # 加工时间最大值

# 生成随机数据
np.random.seed(1) # 设置随机种子

def produceData(n, m, low, high):
    data = np.zeros([m, n], dtype=int)
    data[:] = np.random.uniform(low, high + 1, [m, n])
    data = data.T
    return data

t = produceData(n,m,low,high) # 每个工件在每台机器上的加工时间

start_time = time.time() # 记录开始时间

# 创建模型
model = Model('FSP')

# 创建变量
x = model.addVars(n,n,vtype=GRB.BINARY,name='x')

C = model.addVars(n,m,vtype=GRB.CONTINUOUS,name='C')

makespan = model.addVar(vtype=GRB.CONTINUOUS,name='makespan')

# 设置目标函数
model.addConstrs(makespan >= C[k,m-1] for k in range(n))

model.setObjective(makespan, GRB.MINIMIZE)

# 约束条件
model.addConstrs(quicksum(x[i,k] for k in range(n))==1 for i in range(n))

model.addConstrs(quicksum(x[i,k] for i in range(n))==1 for k in range(n))

model.addConstr(C[0,0] >= quicksum(x[i,0] * t[i][0] for i in range(n)))

model.addConstrs(C[k+1,j] >= C[k,j] + quicksum(x[i,k+1] * t[i][j] for i in range(n)) for k in range(n-1) for j in range(m))

model.addConstrs(C[k,j+1] >= C[k,j] + quicksum(x[i,k] * t[i][j+1] for i in range(n)) for k in range(n) for j in range(m-1))

model.addConstrs(C[k,j] >= 0 for k in range(n) for j in range(m))

# 设置求解器的最长运行时间为1小时（3600s）
model.setParam(GRB.Param.TimeLimit,3600)

# 模型求解
model.optimize()

# 记录结束时间
end_time = time.time()
solve_time = end_time - start_time

# 打印结果
if model.status == GRB.OPTIMAL:
    print('最优解：')
    for i in range(n):
        for k in range(n):
            if x[i,k].x > 0.5:
                sequence.append(k)
                print(f"{i}是排列Π的第{k}个工件")
    print('工件的加工次序：',sequence)
    print('总完成时间：',model.objVal)
elif model.status == GRB.Status.TIME_LIMIT:
    print('目标函数值上界：',model.objVal,'目标函数值下界：',model.ObjBound)
else:
    print('无可行解')
print("求解时间：",solve_time,'s')

5.2遗传算法（GA）求解FSP

import numpy as np
import random
import matplotlib.pyplot as plt

# 辅助函数
def produceData(n,m,low,high):
	"""
	生成流水车间作业数据
	:param n: 工序数目
	:param m: 机器数目
	:param low: 加工时间最小值
	:param high: 加工时间最大值
	"""
	data = np.zeros([m + 1, n], dtype=int)
	data[0] = np.arange(n)
	data[1:] = np.random.uniform(low, high + 1, [m, n])
	return data

def makespan(data):
	"""
	每个工件在每台机器上的完成时间
	:param data: m行n列，第1行工序编号，值加工时间
	"""
	makespan = np.zeros_like(data)
	for i in range(makespan.shape[0]):
		for j in range(makespan.shape[1]):
			if i == 0:
				makespan[i, j] = data[i, j]
			if i == 1:
				makespan[i, j] = np.sum(data[1, :j + 1])
			if j == 0 and i != 0:
				makespan[i, j] = np.sum(data[1:i + 1, j])
	for i in range(2, makespan.shape[0]):
		for j in range(1, makespan.shape[1]):
			makespan[i, j] = data[i, j] + max(makespan[i, j - 1], makespan[i - 1, j])
	return makespan

def makespan_value(data):
	"""
	最大生产流程时间
	:param data: m行n列，第1行工序编号，值加工时间
	"""
	makespan_value = makespan(data)[-1, -1]
	return makespan_value

# 生成初始种群
def johnson(data):
	# 分组
	P = data[:,np.where(data[1] < data[2])[0]]
	Q = data[:,np.where(data[1] >= data[2])[0]]
	# 排序
	P = P[:,np.argsort(P[1])]
	Q = Q[:,np.argsort(-Q[2])]
	# 组合
	sequence = np.hstack([P[0],Q[0]])
	return sequence

def cds(data):
	# 分组，将m台机器的问题分解为为m-1组两机器的问题
	data_group = np.zeros([data.shape[0] - 2, 3, data.shape[1]])
	for i in range(data_group.shape[0]):
		data_group[i, 0] = data[0]
		for j in range(data.shape[1]):
			data_group[i, 1, j] = np.sum(data[1:i + 2, j])
			data_group[i, 2, j] = np.sum(data[-i - 1:, j])
	# 对每组分别运用johnson算法，找到每组的最优排列
	data_johnson = np.zeros([data_group.shape[0], data_group.shape[2]])
	for i in range(data_group.shape[0]):
		data_johnson[i] = johnson(data_group[i])
	sequences = np.array(data_johnson, dtype=int)
	return sequences

def ra(data):
	# 分组，将原问题转化为一个双机调度问题
	group_data = np.zeros([3, data.shape[1]], dtype=data.dtype)
	group_data[0] = data[0]
	for i in range(1, data.shape[0]):
		for j in range(data.shape[1]):
			group_data[1, j] += (data.shape[0] - i) * data[i, j]
			group_data[2, j] += i * data[i, j]
	# 运用johnson算法找到最优排列
	ra_data = johnson(group_data)
	return ra_data

def exchangeMutation(individual):
	mutated_individual = individual.copy()
	pos1,pos2 = random.sample(range(len(individual)),2) # 随机选取两个交换点
	mutated_individual[pos1],mutated_individual[pos2] = mutated_individual[pos2],mutated_individual[pos1] # 交换基因
	return mutated_individual

def generatePopulation(popSize,data):
	pop = np.zeros([popSize,data.shape[1]],dtype=int)
	machineNum = data.shape[0] - 1 # 机器数
	pop[:machineNum-1] = cds(data) # 使用cds方法生成前m-1个
	pop[machineNum-1] = ra(data) # 使用ra方法生成第m个
	for i in range(popSize-machineNum): # 剩下的个体从已经生成的个体中随机选择然后进行交换变异产生
		a = random.randint(0,machineNum-1)
		pop[machineNum] = exchangeMutation(pop[a])
		machineNum += 1
	return pop

# 适应度函数
def fitness(popSize,data,pop):
	fitness = np.zeros([popSize,1])
	makeSpan = np.zeros([popSize,1])
	for i in range(popSize):
		makeSpan[i] = makespan_value(data[:,pop[i]])
	max_makeSpan = np.max(makeSpan) # 计算每代种群中最大的最大完工时间
	for i in range(popSize):
		fitness[i] = max_makeSpan - makeSpan[i]
	return fitness

# 选择操作
def select(popSize,fitness):
	'''
	比例选择
	'''
	selectProbability = np.zeros([popSize,1])
	totalFitness = np.sum(fitness)
	for i in range(popSize):
		selectProbability[i] = fitness[i] / totalFitness # 最大完工时间越小的个体被选中的概率越大
	selectProbability_1d = selectProbability.flatten() # 降维
	return selectProbability_1d

# 交叉操作
def lox(parents):
	'''
	线性次序交叉（LOX）
	'''
	parent1 = parents[0]
	parent2 = parents[1]
	# 随机生成两个交叉点
	size = len(parent1)
	crossoverPoints = sorted(np.random.choice(size,2,replace=False))
	# 初始化子代
	child1 = np.full(size,-1,dtype=int)
	child2 = np.full(size,-1,dtype=int)
	# 复制交叉点之间的片段到子代
	child1[crossoverPoints[0]:crossoverPoints[1]] = parent2[crossoverPoints[0]:crossoverPoints[1]]
	child2[crossoverPoints[0]:crossoverPoints[1]] = parent1[crossoverPoints[0]:crossoverPoints[1]]
	# 填充剩余的位置
	pointer1 = crossoverPoints[1]
	pointer2 = crossoverPoints[1]
	for i in range(size):
		if parent1[i] not in child1:
			child1[pointer1] = parent1[i]
			pointer1 = (pointer1 + 1) % size
		if parent2[i] not in child2:
			child2[pointer2] = parent2[i]
			pointer2 = (pointer2 + 1) % size
	return child1,child2

def crossover(popSize,pop,fitness,Pc):
	pop_children = pop.copy()
	selectProbability = select(popSize,fitness) # 种群中每个个体被选中的概率
	individualNum = 0
	while individualNum < popSize - 2:
		if random.random() < Pc:
			parents_indices = np.random.choice(popSize,size=2,replace=False,p=selectProbability) # 依据概率随机选择两个进行交叉的父代个体
			parents = pop[parents_indices]
			children = lox(parents)
			pop_children[individualNum] = children[0]
			pop_children[individualNum + 1] = children[1]
			individualNum += 2
	return pop_children

# 变异操作
def shiftMutation(individual,Pm):
	'''
	移位变异操作
	'''
	mutated_individual = individual.copy() # 复制输入个体以防止修改原始个体
	for i in range(len(mutated_individual)): # 对于个体中的每个基因都有Pm的变异概率
		if random.random() < Pm:
			index = random.randint(0,len(mutated_individual) - 1) # 随机选择一个基因的位置
			# 移位操作
			gene = mutated_individual[i] # 被移位的基因
			mutated_individual = np.delete(mutated_individual,i) # 从当前位置移除元素
			mutated_individual = np.insert(mutated_individual,index,gene) # 插入元素到新位置
	return mutated_individual

def mutation(pop,popSize,Pm):
	# 对种群中的每一个个体运用移位变异操作
	for i in range(popSize):
		pop[i] = shiftMutation(pop[i],Pm)
	return pop

def elite_reserved(fitness,pop,data):
	'''
	精英保留策略
	'''
	elite_population = np.zeros([2,data.shape[1]],dtype=int)
	# 选取出种群中适应度最大的两个个体
	elite_indices = np.argsort(fitness[:, 0])[-2:]
	elite_individuals = [pop[i] for i in elite_indices]
	elite_population[0] = elite_individuals[0]
	elite_population[1] = elite_individuals[1]
	return elite_population


# 遗传算法运行参数
popSize = 100 # 种群规模
generation = 100 # 迭代次数
Pc = 1 # 交叉概率
Pm = 0.05 # 变异概率
np.random.seed(1) # 设置随机种子
produceTime = produceData(10,10,1,99) # 每个工件在各台机器上的加工时间
population = generatePopulation(popSize,produceTime) # 初始种群

# 遗传算法主程序
pop_trace = np.zeros([generation,3])
individual_trace = np.zeros([generation,produceTime.shape[1]],dtype=int)
best_times = []
for g in range(generation):
	fitness_value = fitness(popSize, produceTime, population) # 计算各个个体的适应度
	elite_population = elite_reserved(fitness_value,population,produceTime) # 保留下每一代中的精英个体
	pop_trace[g] = [g,np.mean(fitness_value),np.max(fitness_value)] # 记录下每一代种群的平均适应度和最大适应度
	individual_trace[g] = population[np.argmax(fitness_value)] # 记录下每代群体中适应度最大的个体
	crossover_children = crossover(popSize,population,fitness_value,Pc) # 对种群进行交叉操作
	population = mutation(crossover_children, popSize, Pm) # 对种群进行变异操作
	# 将保留下来的精英个体直接保存到下一代种群中
	population[popSize-2] = elite_population[0]
	population[popSize-1] = elite_population[1]
	best_time = makespan_value(produceTime[:,individual_trace[g]]) # 计算每代群体中适应度最大的个体的最大完工时间
	best_times.append(best_time)
	print(f'第{g+1}代的工件加工次序为：{individual_trace[g]}，最大完工时间为：{best_time}')
best_individual = individual_trace[np.argmin(best_times)]
print("最优的工件加工次序为：",best_individual,end='，')
print("最小的最大完工时间为：",makespan_value(produceTime[:,best_individual]))

# 画迭代图
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False

plt.plot(range(1,generation + 1),best_times)
plt.xlabel('迭代次数')
plt.ylabel('最大完工时间')
plt.title('优化过程',fontsize=15)
plt.show()

参考文献

[1]ETILER O, TOKLU B, ATAK M, 等. A genetic algorithm for flow shop scheduling problems[J/OL]. Journal of the Operational Research Society, 2004, 55(8): 830-835. DOI:10.1057/palgrave.jors.2601766.

[2]CAMPBELL H G, DUDEK R A, WORK(S): M L S R. A Heuristic Algorithm for the n Job, m Machine Sequencing Problem[J]. Management Science, 1970, 16(10,): B630-B637.

[3]CHEN C L, VEMPATI V S, ALJABER N. An application of genetic algorithms for flow shop problems[J/OL]. European Journal of Operational Research, 1995, 80(2): 389-396. DOI:10.1016/0377-2217(93)E0228-P.

[4]DANNENBRING D G. An Evaluation of Flow Shop Sequencing Heuristics[J]. Management Science, 1977, 23(11): 1174-1182.