机器学习算法实战案例：使用 Transformer 进行时间序列预测

自 ChatGPT 问世以来，大型语言模型（LLMs）已经引起巨大轰动，取得的成果令人印象深刻。LLMs 成功的关键在于它们的核心构建模块，即 transformers。

在本文中，我们将提供一个在 PyTorch 中使用它们的完整指南，特别关注时间序列预测。

在本文中，我们将从理论介绍 transformers 开始，然后转向在 PyTorch 中应用它们。

为此，我们将讨论一个选定的例子，即预测正弦函数。我们将展示如何生成这个函数的数据并正确预处理它，然后使用 transformers 学习如何预测这个函数。

稍后，我们将讨论在未来标记不可用时如何进行推断，并通过将示例扩展到多维数据。

机器学习算法实战案例系列

• 机器学习算法实战案例：确实可以封神了，时间序列预测算法最全总结！

• 机器学习算法实战案例：时间序列数据最全的预处理方法总结

• 机器学习算法实战案例：GRU 实现多变量多步光伏预测

• 机器学习算法实战案例：LSTM实现单变量滚动风电预测

• 机器学习算法实战案例：LSTM实现多变量多步负荷预测

• 机器学习算法实战案例：CNN-LSTM实现多变量多步光伏预测

• 机器学习算法实战案例：BiLSTM实现多变量多步光伏预测

• 机器学习算法实战案例：VMD-LSTM实现单变量多步光伏预测

• 机器学习算法实战案例：VMD-LSTM实现单变量多步光伏预测(升级版)

• 机器学习算法实战案例：Informer实现多变量负荷预测

答疑&技术交流

技术要学会分享、交流，不建议闭门造车。一个人可以走的很快、一堆人可以走的更远。

本文完整代码、相关资料、技术交流&答疑，均可加我们的交流群获取，群友已超过2000人，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友。

?方式①、微信搜索公众号：Python学习与数据挖掘，后台回复：加群
方式②、添加微信号：dkl88194，备注：来自CSDN + 技术交流

Transformer 简介

本文的目标是提供一个完整的使用 transformers 的教程，而不是在理论上介绍和解释这些有趣的模型。

为了完整起见，我们将对 transformers 进行简要的介绍。Transformers 由一个编码器和一个解码器组成。编码器处理输入序列，解码器输出输出序列。一个主要的例子是机器翻译，例如从法语翻译成英语：

概述

输入和输出序列，顾名思义，由多个值或标记组成。与逐个处理数据的循环神经网络（RNN）不同，transformers同时处理所有这些数据（这是它们的优势之一）。

为此，每个标记都被编码/嵌入到一个更高维度以进行未来处理。然后，我们为这个嵌入添加一些位置编码，这是至关重要的，因为标记是并行处理的，没有这个，transformer 将无法理解数据的顺序。

更深入地挖掘

让我们可视化编码器的输入：

如上所述，每个输入标记都被嵌入，并添加位置编码，得到编码器的输入。

接下来，让我们来看一下单个编码器层的内部：

我们看到了自注意和一个前馈层的块。首先，通过自注意，对于每个标记，我们生成其他标记的压缩表示其上下文。核心是三个值：查询(Q)、键(K)和值(V)，它们是通过对当前输入标记进行矩阵乘法获得的。

给定一个标记作为查询，我们使用所有其他标记的键值来确定这些标记的分数。然后，我们通过它们的值将这些分数相乘，并进行聚合。

现在来看一下图示：

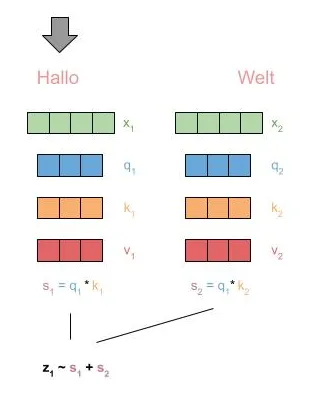
在实践中，transformer 使用多头注意力（Multi-head Attention，MHA），这简单地意味着以上过程重复执行 N 次，并将得到的值连接起来。

接下来是前馈块，它只是一个处理上一步输出值的全连接层。

这完成了一个编码器块 —— 我们重复这个块多次（在原始论文中是 6 次）。

在解码器方面，我们也是一样 —— 即也堆叠了 M 个由自注意力和前馈层组成的解码器层。如前所述，与编码器的区别在于：

1. 我们还会关注最后一个编码器层的所有生成表示。
2. 我们在自注意力步骤中屏蔽值。即在解码标记 i 时，我们不能关注标记 i+1、i+2 等，以避免作弊并简单地复制未来的输出。

总体而言，在简化的形式下，完整的模型可以被可视化如下：

在这些理论基础已经奠定的基础上，让我们转向在 Pytorch 中使用 transformer 模型。如果你对一切还不是非常清楚，继续下去可能是值得的，也许看到应用的东西有助于理解它。

Pytorch 中的 Transformers

在这一部分，我们将展示如何在 Pytorch 中使用 transformers，使用现有的 transformer 模块。由于模型已经实现，主要的“困难”在于预处理输入和输出，并以正确的方式使用 transformer。

我们希望训练我们的 transformer 模型来预测一个带噪声的正弦函数。在本文末尾，我们将展示如何将此扩展到多维输入和输出。

让我们创建一个名为 sine_generator.py 的脚本来生成我们的训练数据，并将其保存到磁盘，以便我们以后可以加载它：

from pathlib import Path
import numpy as np

def generate_data(data_path: Path, num_steps: int, interval: float = 0.1) -> None:
    x = np.linspace(0, num_steps * interval, num_steps)
    y = np.sin(x) + np.random.normal(0, 0.1, x.shape)

    np.savez(data_path, y=y)

generate_data("data.npz", 1000000)

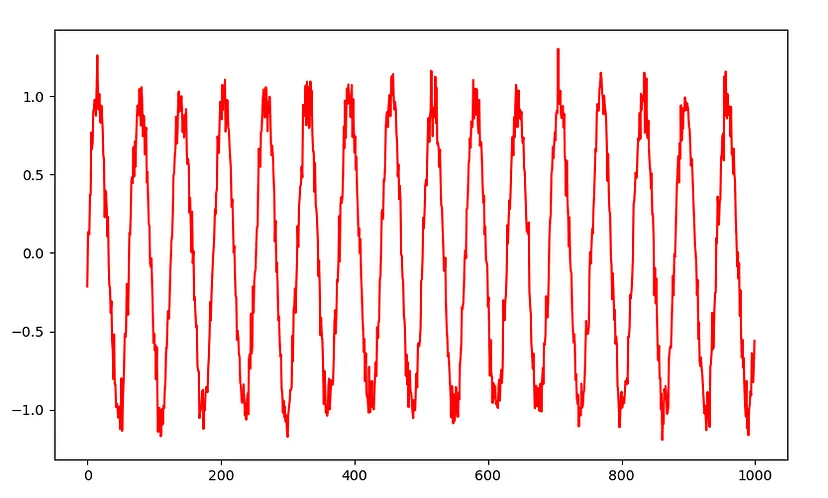
因此，我们生成了1,000,000个带噪声的正弦曲线数据点，可能如下所示：

模型

使用 Pytorch 初始化模型实际上非常简单——我们可以直接使用可用的 Transformer 模型，并在我们的代码中使用它：

self.transformer = torch.nn.Transformer(nhead=num_heads, num_encoder_layers=num_layers, num_decoder_layers=num_layers, d_model=embed_dim, batch_first=True)

正如我们所看到的，我们指定了头的数量、编码器/解码器层数、我们将馈送到 transformer 的嵌入/特征维度，并指定输入/输出以批次维度开头。

如果我们想要自定义此行为或仅使用模型的部分，可以单独使用编码器和解码器——但是对于我们的用例，完整的变压器已经足够。

准备数据

如前所述，这一部分和接下来的一部分可能是关于在实践中使用 transformer 并使其“运作”最有见地和相关的。首先，我们需要预处理和准备我们的数据，特别是决定什么是输入和输出。

让我们以机器翻译的例子开始：在这个例子中，我们有一个源（src）和一个目标（tgt）序列——src是德语中的原始句子，tgt是其英语翻译。

然后，编码器的输入是src——即由N个标记组成的序列。自然，一切都是批处理的，因此形状将是[bs，N，feat_dim]——并且您可能需要对一些句子进行填充。

我们期望解码器生成的形状为[bs，M，feat_dim]。然而，解码器的输入是tgt向右移动一个——否则解码器可能只是通过每个步骤将输入标记传递到输出。以下图形直观地说明了这一点：

因此，在机器翻译和其他NLP任务中，解码器以特殊令牌开始。

对于我们的例子，我们可以做类似的事情，但在这里我们跟随[2]并使用src的最后一个标记开始解码器输入。

我们在代码中这样做：

def split_sequence(
    sequence: np.ndarray, ratio: float = 0.8
) -> tuple[torch.Tensor, torch.Tensor, torch.Tensor]:
    """Splits a sequence into 2 (3) parts, as is required by our transformer
    model.

    Assume our sequence length is L, we then split this into src of length N
    and tgt_y of length M, with N + M = L.
    src, the first part of the input sequence, is the input to the encoder, and we
    expect the decoder to predict tgt_y, the second part of the input sequence.
    In addition we generate tgt, which is tgt_y but "shifted left" by one - i.e. it
    starts with the last token of src, and ends with the second-last token in tgt_y.
    This sequence will be the input to the decoder.

    Args:
        sequence: batched input sequences to split [bs, seq_len, num_features]
        ratio: split ratio, N = ratio * L

    Returns:
        tuple[torch.Tensor, torch.Tensor, torch.Tensor]: src, tgt, tgt_y
    """
    src_end = int(sequence.shape[1] * ratio)
    # [bs, src_seq_len, num_features]
    src = sequence[:, :src_end]
    # [bs, tgt_seq_len, num_features]
    tgt = sequence[:, src_end - 1 : -1]
    # [bs, tgt_seq_len, num_features]
    tgt_y = sequence[:, src_end:]

    return src, tgt, tgt_y

嵌入、位置编码和掩码

现在我们需要实际将数据馈送到 transformer。为此，我们首先需要嵌入我们的输入——即从1D正弦信号映射到更高的维度——即我们在初始化变压器时指定的维度。有几种方法可以做到这一点，但在这里我们简单地使用一个线性层：

embedding = torch.nn.Linear(
    in_features=in_dim, out_features=embed_dim
)

seq = embedding(seq)

接下来，我们需要应用位置编码。这在Pytorch中并不是一部分（但有很多很好的实现，例如官方文档中的实现）：

# 取自 https://pytorch.org/tutorials/beginner/transformer_tutorial.html，
# 只是修改了以适应 "batch first"。
class PositionalEncoding(torch.nn.Module):
    def __init__(self, d_model: int, dropout: float = 0.1, max_len: int = 5000) -> None:
        super().__init__()
        self.dropout = torch.nn.Dropout(p=dropout)

        position = torch.arange(max_len).unsqueeze(1)
        div_term = torch.exp(
            torch.arange(0, d_model, 2) * (-math.log(10000.0) / d_model)
        )
        pe = torch.zeros(1, max_len, d_model)
        pe[0, :, 0::2] = torch.sin(position * div_term)
        pe[0, :, 1::2] = torch.cos(position * div_term)
        self.register_buffer("pe", pe)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        """Adds positional encoding to the given tensor.

        Args:
            x: tensor to add PE to [bs, seq_len, embed_dim]

        Returns:
            torch.Tensor: tensor with PE [bs, seq_len, embed_dim]
        """
        x = x + self.pe[:, : x.size(1)]
        return self.dropout(x)

有了这个，我们的输入序列被处理如下：

src = self.encoder_embedding(src)
src = self.positional_encoding(src)

在解码器方面，我们执行相同的步骤，但另外生成一个掩码以避免关注未来的时间步：

# 生成掩码以避免关注未来的输出。
# [tgt_seq_len, tgt_seq_len]
tgt_mask = torch.nn.Transformer.generate_square_subsequent_mask(tgt.shape[1])
# 嵌入解码器输入并添加位置编码。
# [bs, tgt_seq_len, embed_dim]
tgt = self.decoder_embedding(tgt)
tgt = self.positional_encoding(tgt)

生成的掩码是一个方阵，其中第i行指定允许哪些标记j参与关注——因此，掩码实际上是一个“向右移动”的对角阵。

现在，让我们将所有内容放在一起，训练我们的模型并可视化结果。

完整的模型（model.py）如下所示

import math
import torch

# 取自 https://pytorch.org/tutorials/beginner/transformer_tutorial.html，
# 只是修改了以适应 "batch first"。
class PositionalEncoding(torch.nn.Module):
    def __init__(self, d_model: int, dropout: float = 0.1, max_len: int = 5000) -> None:
        super().__init__()
        self.dropout = torch.nn.Dropout(p=dropout)

        position = torch.arange(max_len).unsqueeze(1)
        div_term = torch.exp(
            torch.arange(0, d_model, 2) * (-math.log(10000.0) / d_model)
        )
        pe = torch.zeros(1, max_len, d_model)
        pe[0, :, 0::2] = torch.sin(position * div_term)
        pe[0, :, 1::2] = torch.cos(position * div_term)
        self.register_buffer("pe", pe)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        """Adds positional encoding to the given tensor.

        Args:
            x: tensor to add PE to [bs, seq_len, embed_dim]

        Returns:
            torch.Tensor: tensor with PE [bs, seq_len, embed_dim]
        """
        x = x + self.pe[:, : x.size(1)]
        return self.dropout(x)


class TransformerWithPE(torch.nn.Module):
    def __init__(
        self, in_dim: int, out_dim: int, embed_dim: int, num_heads: int, num_layers: int
    ) -> None:
        """Initializes a transformer model with positional encoding.

        Args:
            in_dim: number of input features
            out_dim: number of features to predict
            embed_dim: embed features to this dimension
            num_heads: number of transformer heads
            num_layers: number of encoder and decoder layers
        """
        super().__init__()

        self.positional_encoding = PositionalEncoding(embed_dim)

        self.encoder_embedding = torch.nn.Linear(
            in_features=in_dim, out_features=embed_dim
        )
        self.decoder_embedding = torch.nn.Linear(
            in_features=out_dim, out_features=embed_dim
        )

        self.output_layer = torch.nn.Linear(in_features=embed_dim, out_features=out_dim)

        self.transformer = torch.nn.Transformer(
            nhead=num_heads,
            num_encoder_layers=num_layers,
            num_decoder_layers=num_layers,
            d_model=embed_dim,
            batch_first=True,
        )

    def forward(self, src: torch.Tensor, tgt: torch.Tensor) -> torch.Tensor:
        """Forward function of the model.

        Args:
            src: input sequence to the encoder [bs, src_seq_len, num_features]
            tgt: input sequence to the decoder [bs, tgt_seq_len, num_features]

        Returns:
            torch.Tensor: predicted sequence [bs, tgt_seq_len, feat_dim]
        """
        # if self.train:
        # Add noise to decoder inputs during training
        # tgt = tgt + torch.normal(0, 0.1, size=tgt.shape).to(tgt.device)

        # Embed encoder input and add positional encoding.
        # [bs, src_seq_len, embed_dim]
        src = self.encoder_embedding(src)
        src = self.positional_encoding(src)

        # Generate mask to avoid attention to future outputs.
        # [tgt_seq_len, tgt_seq_len]
        tgt_mask = torch.nn.Transformer.generate_square_subsequent_mask(tgt.shape[1])
        # Embed decoder input and add positional encoding.
        # [bs, tgt_seq_len, embed_dim]
        tgt = self.decoder_embedding(tgt)
        tgt = self.positional_encoding(tgt)

        # Get prediction from transformer and map to output dimension.
        # [bs, tgt_seq_len, embed_dim]
        pred = self.transformer(src, tgt, tgt_mask=tgt_mask)
        pred = self.output_layer(pred)

        return pred

主要的训练和测试循环（main.py）：

import torch
from torch.utils.data import DataLoader

from model import TransformerWithPE
from utils import (
    load_and_partition_data,
    make_datasets,
    move_to_device,
    split_sequence,
    visualize,
)

BS = 512
FEATURE_DIM = 128
NUM_HEADS = 8
NUM_EPOCHS = 100
NUM_VIS_EXAMPLES = 1
NUM_LAYERS = 2
LR = 0.001

def main() -> None:
    # Load data and generate train and test datasets / dataloaders


    sequences, num_features = load_and_partition_data("data.npz")
    train_set, test_set = make_datasets(sequences)
    train_loader, test_loader = DataLoader(
        train_set, batch_size=BS, shuffle=True
    ), DataLoader(test_set, batch_size=BS, shuffle=False)

    device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

    # Initialize model, optimizer and loss criterion
    model = TransformerWithPE(
        num_features, num_features, FEATURE_DIM, NUM_HEADS, NUM_LAYERS
    ).to(device)
    optimizer = torch.optim.Adam(model.parameters(), lr=LR)
    criterion = torch.nn.MSELoss()

    # Train loop
    for epoch in range(NUM_EPOCHS):
        epoch_loss = 0.0
        for batch in train_loader:
            optimizer.zero_grad()

            src, tgt, tgt_y = split_sequence(batch[0])
            src, tgt, tgt_y = move_to_device(device, src, tgt, tgt_y)
            # [bs, tgt_seq_len, num_features]
            pred = model(src, tgt)
            loss = criterion(pred, tgt_y)
            epoch_loss += loss.item()

            loss.backward()
            optimizer.step()

        print(
            f"Epoch [{epoch + 1}/{NUM_EPOCHS}], Loss: "
            f"{(epoch_loss / len(train_loader)):.4f}"
        )

    # Evaluate model
    model.eval()
    eval_loss = 0.0
    with torch.no_grad():
        for idx, batch in enumerate(test_loader):
            src, tgt, tgt_y = split_sequence(batch[0])
            src, tgt, tgt_y = move_to_device(device, src, tgt, tgt_y)

            # [bs, tgt_seq_len, num_features]
            pred = model(src, tgt)
            loss = criterion(pred, tgt_y)
            eval_loss += loss.item()

            if idx < NUM_VIS_EXAMPLES:
                visualize(src, tgt, pred, pred_infer)

    avg_eval_loss = eval_loss / len(test_loader)
    avg_infer_loss = infer_loss / len(test_loader)

    print(f"Eval Loss on test set: {avg_eval_loss:.4f}")

if __name__ == "__main__":
    main()

在训练了100个epoch之后，我们可视化在保留测试集上得到的预测结果：

在图中，我们以蓝色可视化了输入到编码器的部分，绿色表示模型预测的连续曲线，红色表示实际预测结果。

正如我们所看到的，模型成功学习了预测正弦函数的能力，同时观察到了模型学到的去噪能力，这也很有趣。

推断
关于transformer，经常会出现一个问题，即如何进行推断。是的，到目前为止，我们的模型将会很好地训练，并且在测试集上也会产生良好的结果——也就是说，当模型以编码器/解码器的输入（src/tgt）接收到地面真实数据时，解码器生成的预测将与期望值（tgt_y）非常相似。这种方法称为"teacher forcing"，但这不是在"真实推断"期间发生的事情！

在某个时间点上，我们已经拥有了所有需要的历史数据，现在想要预测时间序列在未来的演变。在这种情况下，自然而然地，我们没有任何输入传递给解码器。

在这种情况下，我们所做的是迭代生成解码器输出：我们从一个空的输出序列开始，其中只有第一个时间步由src的最后一个值填充。然后我们运行一个预测步骤，并将第一步生成的输出插入到输出序列的第2个位置，依此类推。由于我们正确地屏蔽了解码器的输入，输出序列的其余部分是什么样子并不重要（它是空的…）——解码器不使用这些标记。

让我们为我们的模型添加一个推断函数，并修改我们的训练循环以在测试集上运行这个函数：

def infer(self, src: torch.Tensor, tgt_len: int, tgt: torch.Tensor) -> torch.Tensor:
    """Runs inference with the model, meaning: predicts future values
    for an unknown sequence.
    For this, iteratively generate the next output token while
    feeding the already generated ones as input sequence to the decoder.

    Args:
        src: input to the encoder [bs, src_seq_len, num_features]
        tgt_len (int): _description_ - TODO
        tgt (_type_): _description_

    Returns:
        torch.Tensor: inferred sequence
    """
    output = torch.zeros((src.shape[0], tgt_len + 1, src.shape[2])).to(src.device)
    output[:, 0] = src[:, -1]
    for i in range(tgt_len):
        output[:, i + 1] = self.forward(src, output)[:, i]

    return output[:, 1:]

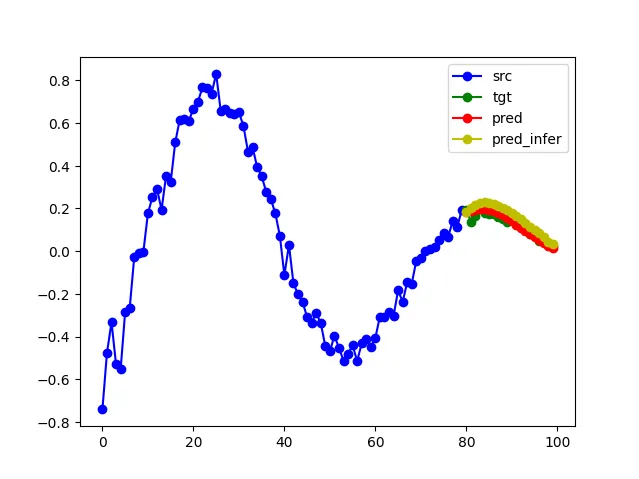
在黄色中，我们现在绘制了通过这种迭代方法生成的预测结果——观察到在这种设置中模型也能够很好地预测函数。

协变量转移

在这个例子中，我们的模型在所有测试任务中都表现得很好。然而，推断和处理引起的测试分布有时可能会导致（很大的）问题。造成这个问题的原因是引入的分布/协变量转移——我们通过从一些训练分布中抽样样本来训练模型，而在运行推断时，模型引起的分布是不同的。

这在模仿学习领域是一个很大的问题，其中一个突出的应用是自动驾驶。实际上，早在90年代初就注意到，一辆训练过的车辆有时会超出边界/超出其已知的训练分布[3]。后来，许多作品都解决了这个问题[4,5]。

在自然语言处理领域，这似乎并没有引起问题——了解为什么对我来说是一个非常有趣的问题。不幸的是，这会超出本文的范围，但一些常见的概念是：语言本质上是多模态的，并且训练数据的数量是庞大的——因此模型实际上永远不会真正“用完”分布——而在模仿学习/自动驾驶中，我们通常只能看到良好驾驶的示例，例如在某些车道中心线周围。

在这里讨论的例子（预测正弦函数）并不是多模态的——但问题可能只是足够简单（或我们预测的序列太短），以便发生分布转移。

因此，我将就此结束，但在这一节中，讨论一遇到协变量转移时可以采取的措施：

1. 使模型不是自回归的：模型“用尽”分布的一个原因是自回归属性，即迭代地生成一个接一个的数据点。对此的一种简单缓解方法是将模型更改为非自回归模型，即一次性预测所有未来的数据点。可以通过删除解码器，并通过一些全连接层来预测tgt的所有点来实现这一点。事实上，ChatGPT之外还有许多语言模型，如BERT或LLama——它们使用不同的体系结构，例如仅编码器和仅解码器（实际上，GPT-3.5是仅解码器的体系结构）。然而，自回归属性是所有（大多数）的共同属性，因此目前这似乎是LLMs的一个成功因素。
2. 添加噪音：这是模仿学习中的一种常用缓解策略，由[5]和[6]推崇。在训练过程中，我们故意向数据添加噪声，使模型接触到不同的分布。在我们的例子中，将噪声添加到解码器的输入可能对模型学习处理不完美序列是有帮助的。

扩展到多维数据
为了总结本文，我们将展示如何将我们的模型扩展到处理多模态、多维数据。然而，这只是更改输入数据并应用相同的模型——因为我们已经设计它能够处理任意数量的输入和输出特征。

我们的多维数据生成如下：我们从两个不同频率的正弦曲线（y1和y2）开始。然后，我们通过叠加（相乘）这些函数来生成y3。

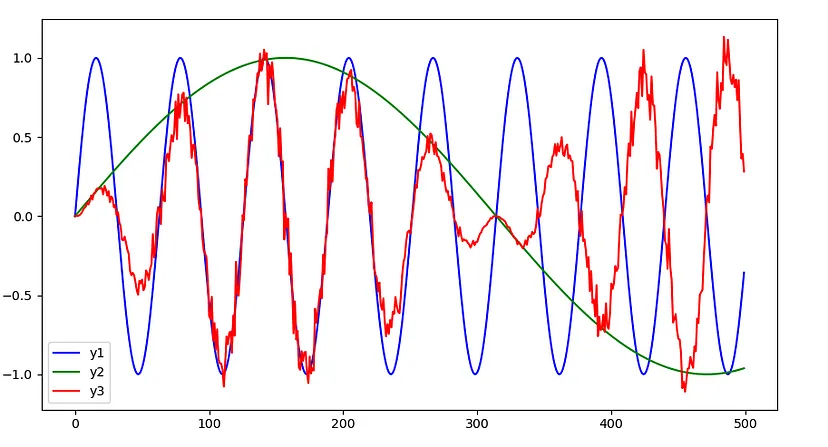
在这种设置中，我们的目标是预测y3。为此，我们将y1和y2视为辅助变量：我们当然可以直接预测y3，但了解y1和y2可能有助于我们和模型更好地理解生成的函数是如何形成的。

考虑到这一点，我们可以对如何建模进行设计选择：

1. 我们只预测y3，将y1和y2视为外生变量（即从外部来源给定）。这样，我们需要解码器来解开y3是如何单独形成的复杂关系，但也将预测减少到我们感兴趣的一个函数。
2. 或者我们可以预测y1、y2和y3。这样，解码器可能更好地学习理解y3是如何形成的（这通常是有益的——请参考：多任务学习）。但我们也在学习纯粹辅助任务的变量上花费了宝贵的编码器容量。

像在机器学习中经常发生的那样，没有对错之分，答案通常是经验性得出的。在这里，我们选择方法2，因为这不需要对模型进行任何更改。但方法1也可以通过进行最小的调整来实现，我邀请您尝试一下。

为了简单起见，在可视化中，我们只显示我们感兴趣的变量y3：

结论

在本文中，我们展示了如何在Pytorch中使用transformer模型。

首先，我们在理论上介绍了transformer。然后，我们转向使用Pytorch在实践中应用它。为了入门，我们选择了一个简单的问题，即预测带噪声的正弦函数。我们展示了如何在Pytorch中初始化transformer，需要什么样的输入和输出形状，以及需要应用哪些其他技术来使其工作（特别是嵌入、位置编码和解码器屏蔽）。接下来，我们讨论了如何运行“真实”推理，当未来的标签不可用时，还简要提到了分布转移的问题。最后，我们展示了如何扩展我们的问题和模型以处理三维数据。

希望您喜欢这篇文章 — 感谢阅读！正如所述，您可以在Github上找到完整的代码。

参考资料

[1] Attention Is All You Need, 2017 (arxiv)

[2] Deep Transformer Models for Time Series Forecasting: The Influenza Prevalence Case, 2020 (arxiv)

[3] ALVINN: AN AUTONOMOUS LAND VEHICLE IN A NEURAL NETWORK, 1988 (NeurIPS proceedings)

[4] A Reduction of Imitation Learning and Structured Prediction to No-Regret Online Learning, 2010 (arxiv)

[5] DART: Noise Injection for Robust Imitation Learning, 2017 (arxiv)

[6] ChauffeurNet: Learning to Drive by Imitating the Best and Synthesizing the Worst, 2018 (arxiv)

[7] https://github.com/hermanmichaels/transformer_example

[8] https://towardsdatascience.com/time-series-prediction-with-transformers-2b64478a4cbd