动态规划算法

动态规划算法

引子

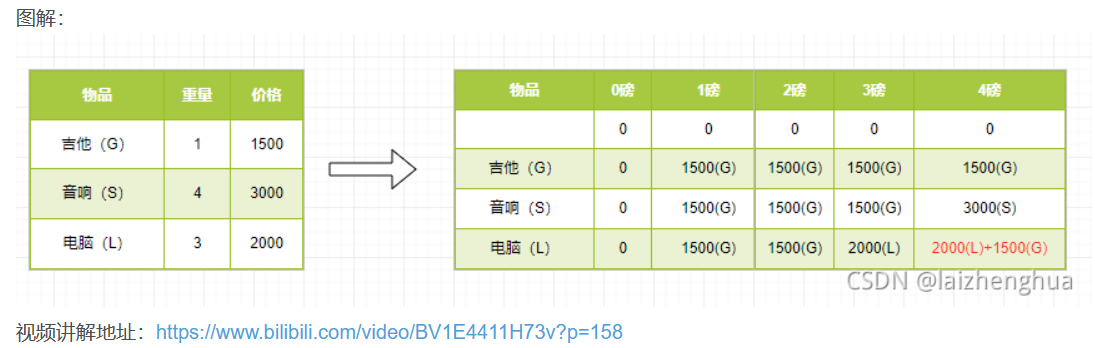
背包问题：现有一个背包，容量为4磅。现有如下物品：

1、要求达到的目标为装入的背包的总价值最大，并且重量不超出

2、要求装入的物品不能重复

3.2、动态规划算法基本介绍
1、动态规划(Dynamic Programming)算法（简称DP算法）的核心思想是：将大问题划分为小问题进行解决，从而一步步获取最优解的处理算法

2、动态规划算法与分治算法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解

3、与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。 ( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解 )

4、动态规划可以通过填表的方式来逐步推进，得到最优解

代码实现背包问题

1、背包问题主要是指一个给定容量的背包、若干具有一定价值和重量的物品，如何选择物品放入背包使物品的价值最大。其中又分 01 背包和完全背包(完全背包指的是：每种物品都有无限件可用)

2、这里的问题属于 01 背包，即每个物品最多放一个。而无限背包可以转化为 01 背包。

3、算法的主要思想：利用动态规划来解决。每次遍历到的第 i 个物品，根据w[i] 和 v[i] 来确定是否需要将该物品放入背包中。即对于给定的 n 个物品，设 v[i]、w[i]分别为第 i 个物品的价值和重量，C 为背包的容量。再令 v[i][j]表示在前 i 个物品中能够装入容量为 j 的背包中的最大价值。

基于以上设定我们得出：

/*
(1) v[i][0]=v[0][j]=0; //表示 填入表 第一行和第一列是 0
(2) 当 w[i]> j时：v[i][j]=v[i-1][j] // 当准备加入新增的商品的容量大于 当前背包的容量时，就直接使用上一个单元格的装入策略
(3) 当 j>=w[i]时： v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]} // 当准备加入的新增的商品的容量小于等于当前背包的容量,装入的方式:
	1. v[i-1][j]： 就是上一个单元格的装入的最大值
	2. v[i]: 表示当前商品的价值
	3. v[i-1][j-w[i]]： 装入 i-1 商品，到剩余空间 j-w[i]的最大值
	4. 当 j>=w[i]时： v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]}
*/

代码示例：

public static void main(String[] args) {
    int[] wight = new int[]{1, 4, 3}; // 物品的重量
    int[] price = new int[]{1500, 3000, 2000}; // 物品的价格
    int m = 4; // 背包的容量
    int n = price.length; // 物品的个数

    // 创建一个二维数组
    // v[i][j] 表示在前i个物品中能够装入容量为j的背包中的最大价值
    int[][] v = new int[n + 1][m + 1];
    // 初始化第一行和第一列，这里在本程序中，可以不去处理，因为默认就是0
    for (int i = 0; i < v.length; i++) {
        v[i][0] = 0; // 将第一列设置为0
    }
    for (int i = 0; i < v.length; i++) {
        v[0][i] = 0; // 将第一行设置为0
    }

    // 为了记录放入商品的情况，我们定一个二维数组
    int[][] path = new int[n + 1][m + 1];

    // 动态规划处理背包问题
    // i和j初始都等于1，目的是不处理第一行第一列
    for (int i = 1; i < v.length; i++) {
        for (int j = 1; j < v[i].length; j++) {
            // 公式
            if (wight[i - 1] > j) { // 因为我们程序i是从1开始的，因此原理公式中的w[i]修改成[i-1]
                v[i][j] = v[i - 1][j];
            } else {
                // 因为 i 是从1开始的，因此公式需要做出调整，如下所示
                // v[i][j] = Math.max(v[i - 1][j], price[i - 1] + v[i - 1][j - wight[i - 1]]);
                if (v[i - 1][j] < price[i - 1] + v[i - 1][j - wight[i - 1]]) {
                    v[i][j] = price[i - 1] + v[i - 1][j - wight[i - 1]];
                    // 把当前的情况记录到path
                    path[i][j] = 1;
                } else {
                    v[i][j] = v[i - 1][j];
                }
            }
        }
    }

    // 输出v
    for (int i = 0; i < v.length; i++) {
        for (int j = 0; j < v[i].length; j++) {
            System.out.print(v[i][j] + " ");
        }
        System.out.println();
    }

    // 输出放入的商品情况
    int i = path.length - 1; // 行的最大下标
    int j = path[0].length - 1; // 列的最大下标
    while (i > 0 && j > 0) {
        if (path[i][j] == 1) {
            System.out.printf("第%d个商品放入到背包\n", i);
            j -= wight[i - 1];
        }
        i--;
    }
}