平衡二分搜索树

王有志，一个分享硬核Java技术的互金摸鱼侠
加入Java人的提桶跑路群：共同富裕的Java人

最近写了点关于Java面试的考点分析，冷落了数据结构与算法一段日子。今天我们一起学习“高级”的二分搜索树–平衡二分搜索树。
数据结构：二分搜索树的最后我们提出了一些问题：

• 计算二分搜索树核心方法的时间复杂度
• 如果数据顺序的插入二分搜索树中，它还具有二分搜索树的特性吗？

先给出第一个问题的答案：二分搜索树中，查找元素的时间复杂度是O(logn)，最坏情况下是O(n)。
练习中有一个问题：实现二分搜索树的前中后序遍历。如果动手实现了中序遍历，就会发现，二分搜索树的中序遍历结果是升（降）序排列的。这是二分搜索树中很重要的特性之一。

二分搜索树的“退化”

如果我们按照由小到大的顺序向二分搜索树中插入数据会发生什么？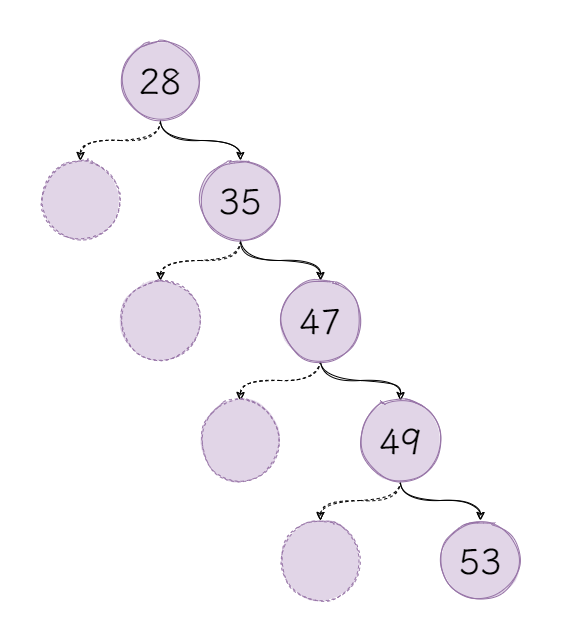

把虚线的部分删掉，不就成了链表吗？随着二分搜索树退化成链表，查找的时间复杂度也来到了O(n)。而且构建出来的二分搜索树左轻右重，那么有没有分布均匀的二分搜索树呢？

平衡二分搜索树

答案是肯定的。有一种二分搜索树，对于任意节点，它的左右子树高度差不超过1，它就是平衡二分搜索树，也称为高度平衡树。
Tips：如果忘了高度的概念，可以回顾数据结构：认识一棵树。
我们先来画两棵树：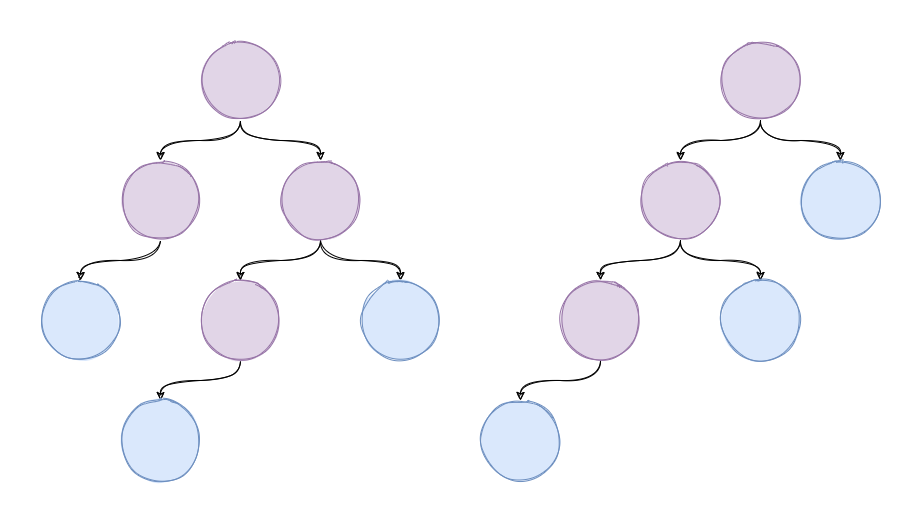

叶子节点标记为蓝色，根据平衡二分搜索树的定义，左侧二叉树中，叶子节点的高度差最大为1，所以它是平衡二分搜索树；右侧二叉树中，最左叶子节点和最右叶子节点的高度差为2，它不是平衡二分搜索树。

平衡因子

我们为每个节点标注它在子树中的高度，有多个高度时，选择最大的高度。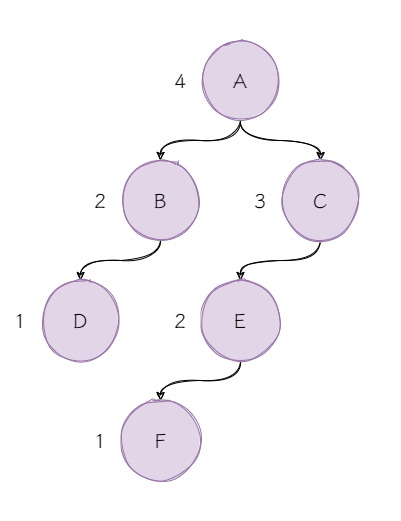

我们来计算平衡因子，平衡因子听起来很高大上，实际上就是左右子树的高度差的绝对值。上图的节点A，其平衡因子是abs(hb?hc)=abs(2?3)=1。
那么它是一棵平衡二分搜索树吗？别忘了，我们强调对于任意节点的左右子树高度差不超过1，那么节点C的高度差是多少呢？
C节点的右子树是空树，空树的高度记为0，那么它的平衡因子是2，不符合平衡二分搜索树的定义。
到这里你可能会想到，不平衡的二分搜索树可以变成平衡二分搜索树吗？

AVL树

1962年，苏联科学家G.M.Adelson-Velsky和Evgenii?Landis发明了最早的自平衡二分搜索树?–?AVL树（Adelson-Velsky?and?Landis?Tree，以科学家命名）。
AVL树的特点是能够自动保持平衡，它通过树旋转来保持平衡。实际上绝大部分的平衡树都是通过树旋转来保持平衡的，也有基于重构（有没有想到数据结构：二分搜索树删除节点时我们的思考过程）的平衡树–替罪羊树。
点击数据结构：平衡二分搜索树，观看AVL树建树过程。
数据结构是通过Data?Structure?Visualization构建的，通过ApowerREC录制。

失衡与旋转

我们看到，随着节点的插入，树的结构产生了变化，导致AVL树失衡。AVL树采用了树旋转的方式恢复平衡。
Tips：关于失衡与旋转的定义目前有些不同的意见。引用维基百科中关于树旋转冲突的部分：

有些人认为旋转方向应该反映节点的移动方向（左子树旋转到父节点的位置为右旋），有些人则认为旋转方向应该反映被旋转的子树是哪棵（左子树旋转到父节点的位置为左旋，与前一种说法相反）。

为了防止冲突引发的歧义，我这里采取《算法精解：C语言描述》中的方法:

• 插入到节点左侧的左侧导致节点失衡的称为LL失衡，恢复平衡的方法称为LL旋转；
• 插入到节点右侧的右侧导致节点失衡的称为RR失衡，恢复平衡的方法称为RR旋转；
• 插入到节点左侧的右侧导致节点失衡的称为LR失衡，恢复平衡的方法称为LR旋转；
• 插入到节点右侧的左侧导致节点失衡的称为RL失衡，恢复平衡的方法称为RL旋转。

看起来好像是绕口令，写得时候也害怕自己打错了。不过不要紧，我们通过图直观的展示这4种失衡的情况：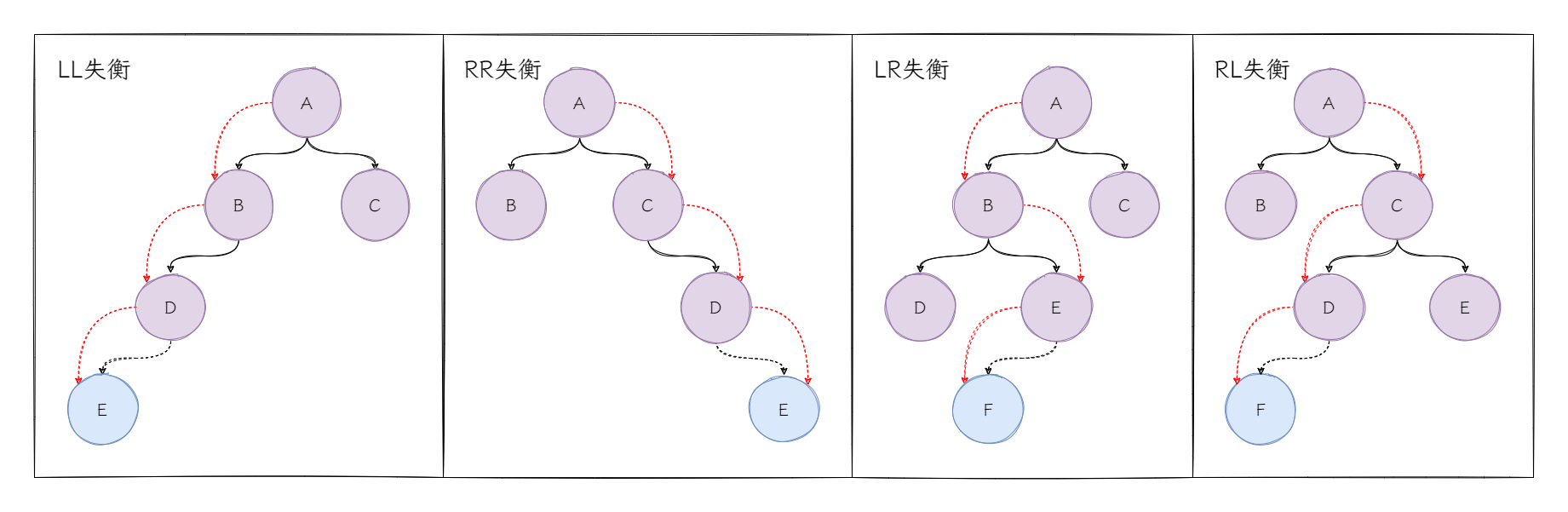

Tips：如何理解左侧？如何理解右侧？
左侧理解为小于，右侧理解为大于，其中第一个左侧/右侧，表示与根节点比较的小于/大于（即在左子树/右子树中插入）。第二个左侧/右侧，表示与左/右子树中任意节点比较的小于/大于。
例如：在A-B-C这棵树左侧的右侧插入节点D。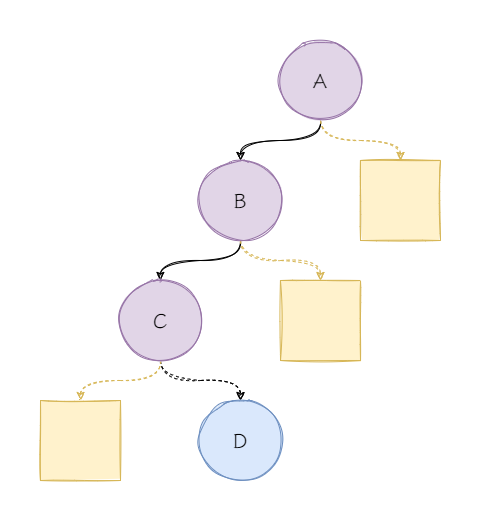

当然，除了插入导致的树失衡，删除也会导致树失衡。例如删除节点C也会导致节点A的平衡因子大于1。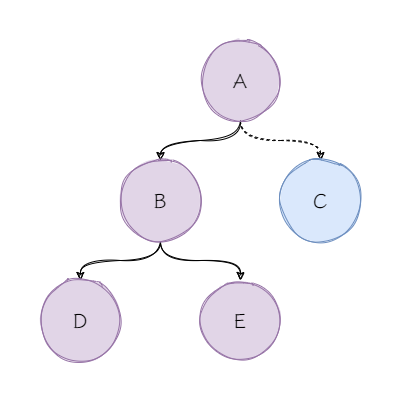

单旋

以删除导致失衡为例，删除节点C后，节点A的左子树的高度为2，右子树为空树，高度为0，以节点A为根节点的平衡二分搜索树失衡。
这时树左重右轻，符合LL失衡的场景，对应的是LL旋转。整体过程也非常简单：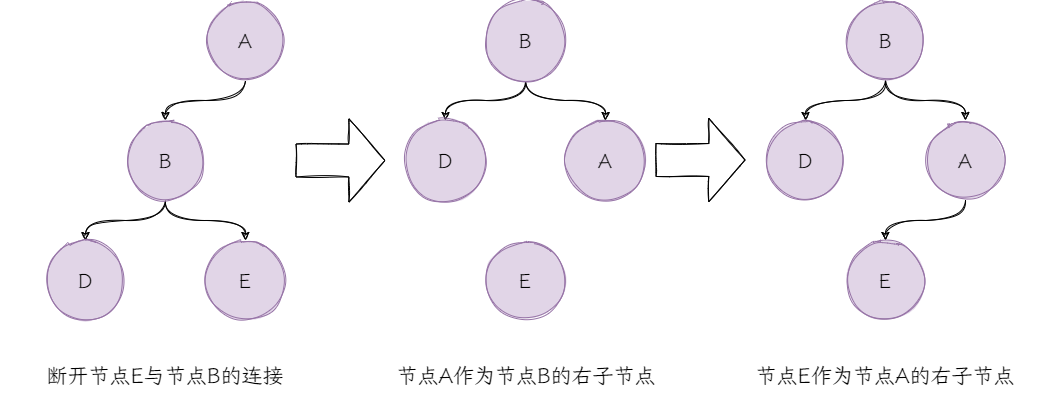

我们通过一段代码描述下LL旋转：

public void rotateLeft(TreeNode<E> root) {
	ThreeNode<E> newRoot = root.getLeftChild();
	ThreeNode<E> tempLeftChild = newRoot.getRightChild();
	newRoot.setRightChild(node);
	root.setLeftChild(tempLeftChild);
	root = newRoot;
}

LL旋转并不能随便进行，它有个非常重要的约束：旋转前后中序遍历的结果不能改变。上图中，旋转前中序遍历的结果是：D→B→E→A，旋转后也保证了中序遍历的结果不变。
Tips：再用这个例子中解释下容易引起歧义的左旋和右旋，毕竟大部分的文章会涉及到左旋和右旋。
从图上看节点B确确实实是向右移动了，而节点A是向“下”移动了，以节点B移动的方向来区分，是右旋没错了。
接着看站队左旋的是怎么解释的：被移动的是节点A的左子树，以谁被移动来看也确实是节点A的左子树被移动了，叫左旋也没问题。
节点A：合着就我没动呗~~
至于RR失衡和RR旋转，就留给大家思考了。

双旋

在单旋的例子中，我们看到的是对“一侧”失衡的旋转，接下来我们看“双侧”失衡的旋转：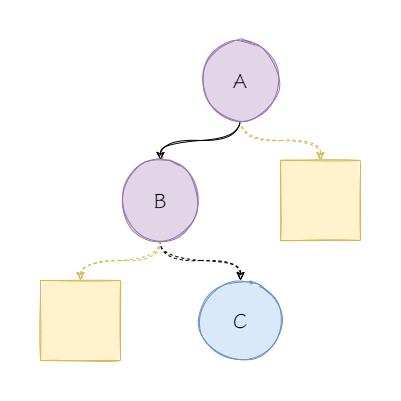

图中的情况很符合我们前面说到的LR失衡的场景，那么我们该如何通过旋转恢复平衡呢？
其实方式很简单既然是L-R两种失衡的方式，那我们就组合两种旋转的方式：

• 先对R失衡的部分进行RR旋转：
• 接着对L失衡的部分进行LL旋转。

首先是对R失衡部分的旋转：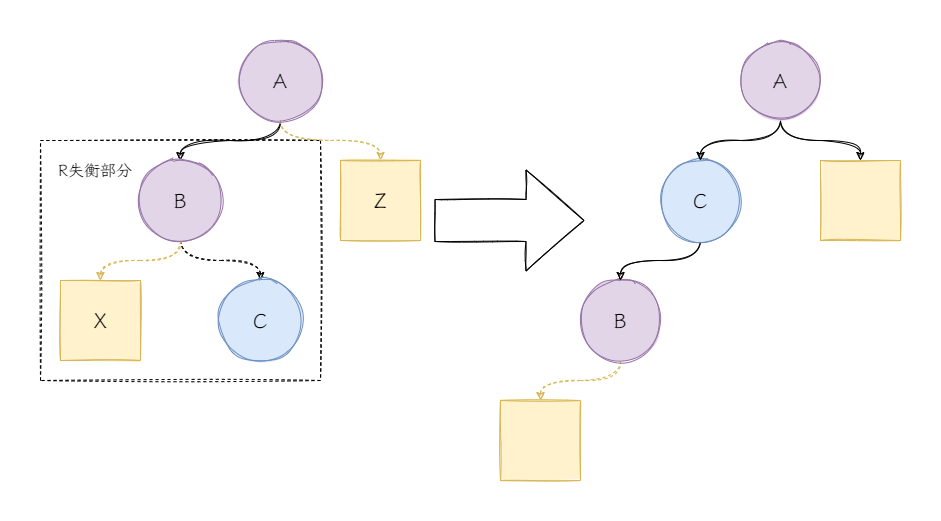

局部RR旋转后就形成了整体的LL失衡，后面的处理方式就再明显不过了吧？
我们来总结下失衡的场景：
LL/RR失衡的场景中，最终造成高度失衡的都是左斜树/右斜树，不是也得是。例如：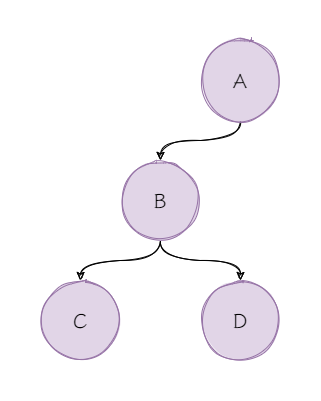

我们既可以看做A-B-C的失衡，也可以看做是A-B-D的失衡，但是哪个失衡好处理呢？
LR/RL失衡的场景中，都是通过对局部L/R失衡的LL/RR旋转形成整体的RR/LL失衡后，再通过RR/LL旋转调整平衡。

结语

今天就先到这里吧，内容并不复杂，也都是偏向理论的内容，我们做个简单的总结：

• 通过二分搜索树的“退化”引出了平衡二分搜索树，然后一起了解了如何通过节点的高度和平衡因子来判定是否属于平衡二分搜索树；
• 引入了AVL树，实现了自动平衡特性的平衡二分搜索树，通常大家称呼这类拥有自动平衡特性的为自平衡二分搜索树；
• 学习了AVL树中导致失衡的场景，以及自动平衡的机制–树旋转的理论基础。

原计划在今天的内容中完成AVL树的实现，不过有小伙伴提议添加Python的实现。

添加Python实现的话内容就会比较多了，方便我再水一篇。虽然Java实现只需要简单的改造下BinarySearchTree就行了，但Python的版本要全部重新实现，所以还是要再写$\frac{shui}{写}$一篇比较好。

---

如果本文对你有帮助的话，还请多多点赞支持。如果文章中出现任何错误，还请批评指正。最后欢迎大家关注分享硬核Java技术的金融摸鱼侠王有志，我们下次再见！