PyTorch官网demo解读——第一个神经网络（1）

神经网络如此神奇，feel the magic

今天分享一下学习PyTorch官网demo的心得，原来实现一个神经网络可以如此简单/简洁/高效，同时也感慨PyTorch如此强大。

这个demo的目的是训练一个识别手写数字的模型！

先上源码：

from pathlib import Path
import requests   # http请求库
import pickle
import gzip

from matplotlib import pyplot   # 显示图像库

import math
import numpy as np
import torch

###########下载训练/验证数据######################################################
# 这里加载的是mnist数据集
DATA_PATH = Path("data")
PATH = DATA_PATH / "mnist"
PATH.mkdir(parents=True, exist_ok=True)

URL = "https://github.com/pytorch/tutorials/raw/main/_static/"
FILENAME = "mnist.pkl.gz"

if not (PATH / FILENAME).exists():
        content = requests.get(URL + FILENAME).content
        (PATH / FILENAME).open("wb").write(content)


###########解压并加载训练数据######################################################
with gzip.open((PATH / FILENAME).as_posix(), "rb") as f:
        ((x_train, y_train), (x_valid, y_valid), _) = pickle.load(f, encoding="latin-1")


# 通过pyplot显示数据集中的第一张图片
# 显示过程会中断运行，看到效果之后可以屏蔽掉，让调试更顺畅
#print("x_train[0]: ", x_train[0])
#pyplot.imshow(x_train[0].reshape((28, 28)), cmap="gray")
#pyplot.show()


# 将加载的数据转成tensor
x_train, y_train, x_valid, y_valid = map(
    torch.tensor, (x_train, y_train, x_valid, y_valid)
)
n, c = x_train.shape   # n是函数，c是列数
print("x_train.shape: ", x_train.shape)
print("y_train.min: {0}, y_train.max: {1}".format(y_train.min(), y_train.max()))


# 初始化权重和偏差值，权重是随机出来的784*10的矩阵，偏差初始化为0
weights = torch.randn(784, 10) / math.sqrt(784)
weights.requires_grad_()
bias = torch.zeros(10, requires_grad=True)

# 激活函数
def log_softmax(x):
    return x - x.exp().sum(-1).log().unsqueeze(-1)

# 定义模型：y = wx + b
# 实际上就是单层的Linear模型
def model(xb):
    return log_softmax(xb @ weights + bias)


# 丢失函数 loss function
def nll(input, target):
    return -input[range(target.shape[0]), target].mean()
loss_func = nll

# 计算精度函数
def accuracy(out, yb):
    preds = torch.argmax(out, dim=1)
    return (preds == yb).float().mean()

###########开始训练##################################################################
bs = 64  # 每一批数据的大小
lr = 0.5  # 学习率
epochs = 2  # how many epochs to train for

for epoch in range(epochs):
    for i in range((n - 1) // bs + 1):
        start_i = i * bs
        end_i = start_i + bs
        xb = x_train[start_i:end_i]
        yb = y_train[start_i:end_i]
        pred = model(xb) # 通过模型预测
        loss = loss_func(pred, yb) # 通过与实际结果比对，计算丢失值

        loss.backward() # 反向传播
        with torch.no_grad():
            weights -= weights.grad * lr  # 调整权重值
            bias -= bias.grad * lr  # 调整偏差值
            weights.grad.zero_()
            bias.grad.zero_()

##########对比一下预测结果############################################################
xb = x_train[0:bs]  # 加载一批数据，这里用的是训练的数据，在实际应用中最好使用没训练过的数据来验证
yb = y_train[0:bs]  # 训练数据对应的正确结果
preds = model(xb)  # 使用训练之后的模型进行预测
print("################## after training ###################")
print("accuracy: ", accuracy(preds, yb))   # 打印出训练之后的精度
# print(preds[0])
print("pred value: ", torch.argmax(preds, dim=1))   # 打印预测的数字
print("real value: ", yb)   # 实际正确的数据，可以直观地和上一行打印地数据进行对比

运行结果：

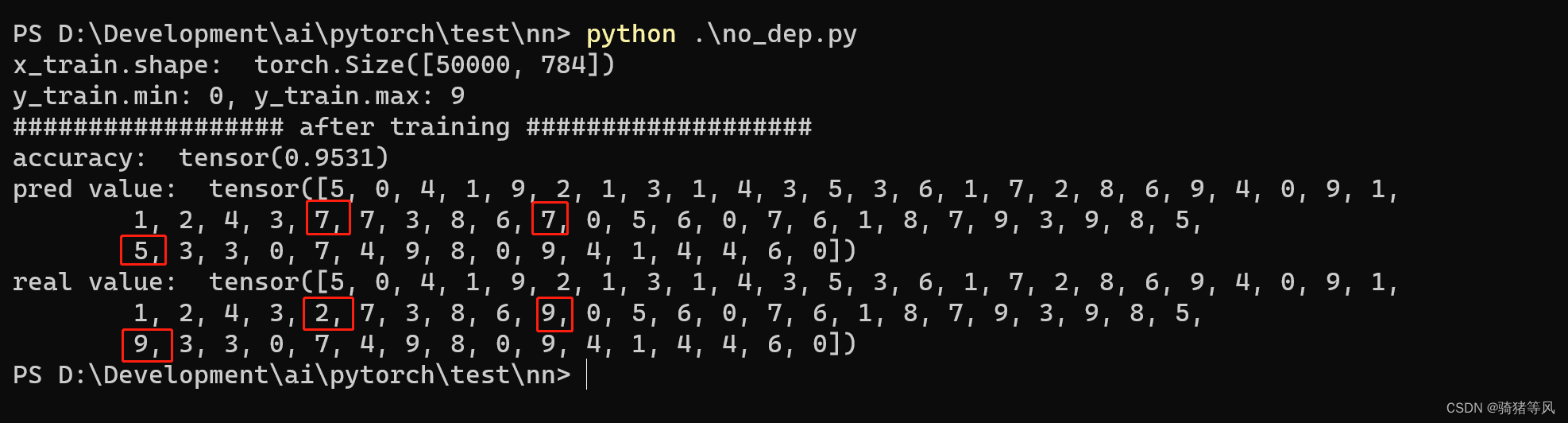
可以看到训练后模型地预测精度达到了0.9531，已经不错了，毕竟只使用了一个单层地Linear模型；从输出地对比数据中可以看出有三个地方预测错了（红框标记地数字）

ok，今天先到这里，下一篇再来解读代码中地细节

附：

PyTorch官方源码：https://github.com/pytorch/tutorials/blob/main/beginner_source/nn_tutorial.py

下一篇：PyTorch官网demo解读——第一个神经网络（2）-CSDN博客

天地一逆旅，同悲万古愁！