MOGWO|多目标灰狼优化算法原理、改进、利用及代码实现（Matlab）

在前面的文章中，作者大多介绍的都是单目标优化算法，然而现实世界的很多问题通常由多个目标组成（比如作者在上一篇文章中介绍的无人机路径规划，各成本函数可以看作不同的目标，若改变成本函数的权值，其规划结果会不同）。

解决多目标问题通常很困难，因为目标之间往往会相互冲突。要使所有目标同时都达到最优往往是不可能实现的。因此，对于多目标问题，需要找到的是一组均衡解，也就是Pareto最优解[1]，使各个目标尽可能达到最优，这个过程即为多目标优化。

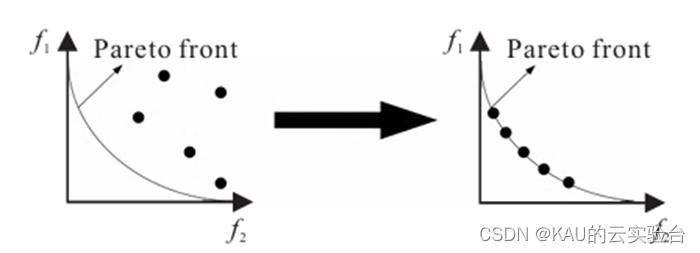
图片来源：进化超多目标优化研究进展及展望

目前，多目标进化算法(Multi-Objective Evolutionary Algorithms，MOEAs)[2]已经取得了飞速的发展，应用在了许多多目标优化问题(multi-objective optimization problems, MOPs)中。

本文中作者将介绍一种高效的多目标优化算法——多目标灰狼优化算法(Multi-Objective Grey Wolf Optimizer，MOGWO)。该算法是由Mirjalili等(灰狼算法的提出者)于2016年提出[2]，发表在中科院一区期刊《expert systems with applications》。

较之GWO，MOGWO主要进行了两个部分的改进：引入存档机制，并改进了头狼选择方式。本文主要包含内容：

MOGWO的原理

改进&利用

MATLAB实现

00 文章目录

1 多目标灰狼优化算法原理

2 改进&利用

3 代码目录

4 算法性能

5 源码获取

01 多目标灰狼优化算法原理

1.1 灰狼优化算法流程

GWO是MOGWO的理论基础，这里简单回顾一下GWO的流程，对GWO不了解的GWO 算法可以看作者的往期文章：

超详细 | 灰狼优化算法原理及其实现(Matlab)

GWO 算法的流程如图所示：

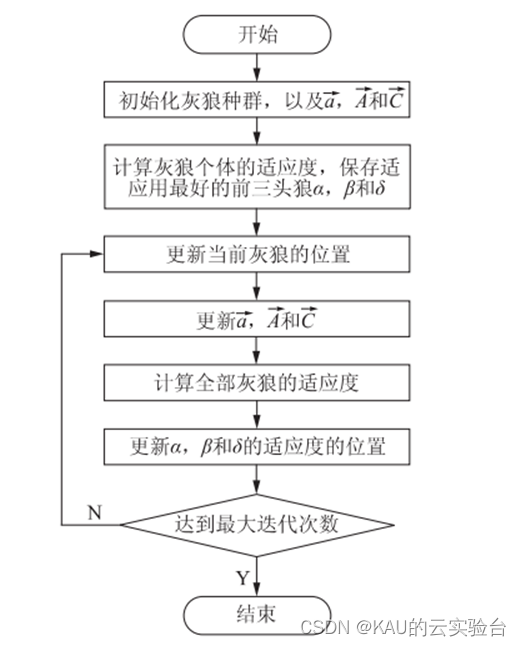
以上是GWO的流程，而MOGWO与GWO最大的不同就是他不能直接选出最优解(多目标)，因此需要重新确定一个解的选择的策略。

1.2 多目标灰狼优化算法

为了将多目标能力添加到GWO算法中，MOGWO在基础灰狼优化算法上增加了两个部分。第一个部分是存档(Archive)，用于存储和检索在优化过程中获得的最合适的非支配解。第二个部分是领导者选择机制，它有助于从存档中保存的解决方案选择α、β和δ。

(这些其实都不是新东西，因为在多目标问题中最大的困难就是如何选择全局引导个体，因此针对这个问题很多学者早已展开研究，MOGWO中的方法最早是在MOPSO中提出[3]，GWO的提出者将这两种策略应用在GWO形成了MOGWO)

这里再插入一个非支配解的解释：Pareto解又称非支配解

设p和q是种群Pop中的两个不同个体，要使得p支配q，需要满足：对所有目标，p不比q差，并至少有一个目标比q好。

而如果p不被任何其他解支配，则p就是Pareto最优解

而Pareto解集中的解都是相互非支配的。

给出一个图示：

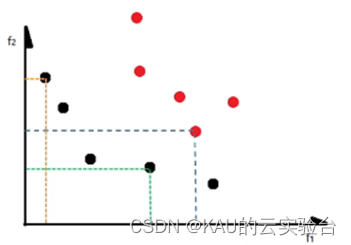
图源：《多目标进化优化》郑金华 邹娟著

其中，黑点都是Pareto最优解，而红点至少被一个黑点支配，黑点组成的集合就是Pareto解集。

下面继续讲解MOGWO:

改进1：存档(Archive)

档案单元里会存储一定数量的非支配解，在迭代过程中，新的非支配解会与档案中的解进行比较，比较的结果有如下情况：

①如果一个新的解被至少一个存档中的解支配，那么这个新的解就不被允许存档。

②如果一个新的解支配了存档中的一个或多个解，那么必须略去被支配的解，新的解就能够存档。

③如果新的解和存档中的解互不支配，则必须将新的解添加到存档中。

若档案中解的数量达到上限，则将运行网格机制来重新安排空间的分割，并找到最拥挤的段来移除一个解，并将新解插入到最不拥挤的段,以维持种群多样性。

网格机制又是什么？

网格机制是用来估计拥挤度的，如下，横轴和纵轴分别代表两个目标函数F1和F2

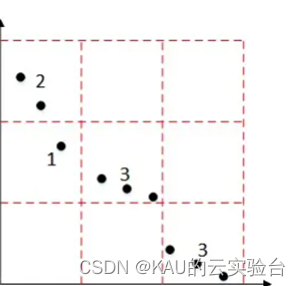
网格机制就是要找出非支配解在每个目标函数的最大值max和最小值min，再将这个区间[min，max]进行N等分，这样就能将所有个体分割在不同网格，而每个解所在的网格中的所有解个数就是它的拥挤度。

改进2：头狼确定

在GWO算法中，头狼(α、β、δ)可以通过目标函数值确定，在MOGWO中,个体的优劣通过Pareto支配关系来确认，头狼选择部分选择搜索空间中最不拥挤的部分，并提供其非支配解作为头狼，而档案中存放着当前的最优解(非支配解)，因此直接从该种群中选择个体作为领头狼，采取轮盘赌的方式从档案中选择个体作为头狼,其计算式如下：

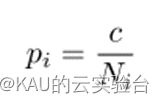
c为常数，Ni为第i段获得的Pareto最优解的数量。由此，可以看到拥挤度越小成为头狼的概率越高。如果在最不拥挤的段少于三个解，则会在第二最小拥挤的段选择。

引入上述两个机制后，MOGWO算法的流程如下：

主体的流程还是和GWO差不多的。（有一个线忘画了，右边剔除拥挤度后的流程紧跟达到最大迭代次数的判断。）

02 改进&利用

2.1 改进

MOGWO的种群位置更新策略本质上和GWO一样，因此也会有和GWO一样的会陷入局部最优解、种群多样性差等问题。因此在GWO中的某些改进策略在MOGWO中仍然适用，如改变线性变化的控制参数a，改进种群初始化策略等。同时，MOGWO选择头狼的机制在目标函数空间尺度大时，收敛性不稳定，并且若存档种群数量大，则其计算量会很大。

2.2 利用

GWO中可对其狼群的围猎机制进行利用，而在MOGWO中，选择头狼的方式是在存档中的多个解中按一定规律进行选择，这种方式类似于精英池的概念，这个思想同样可以用于其他优化算法中，可以避免种群向一个当前最优聚集，从而降低种群陷入局部最优的概率。

03 代码目录

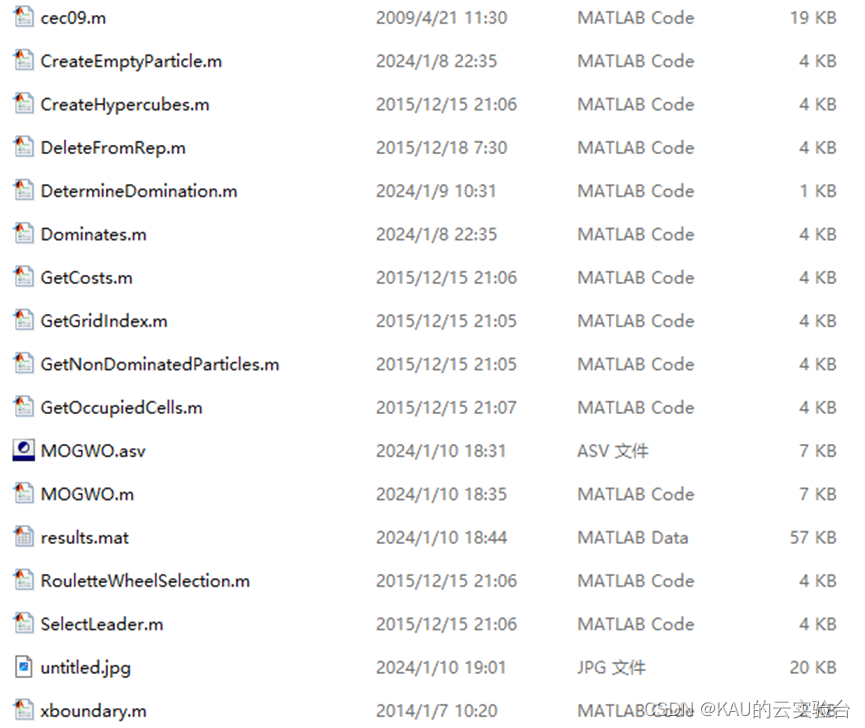
代码注释完整，其中部分MOGWO程序如下：

?

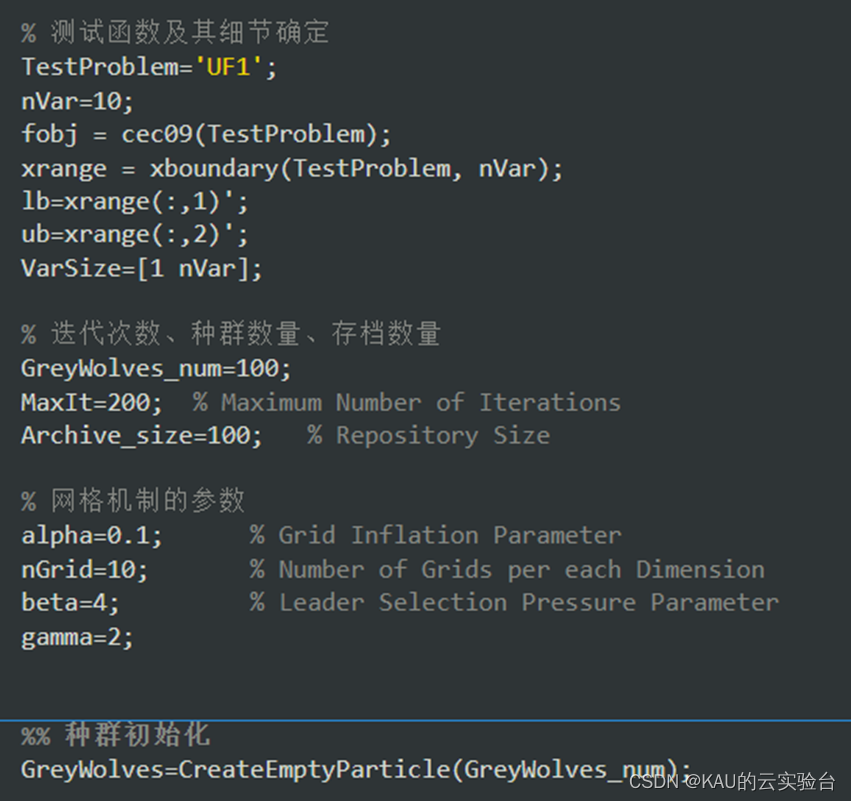
代码获取方式见文末

04 算法性能

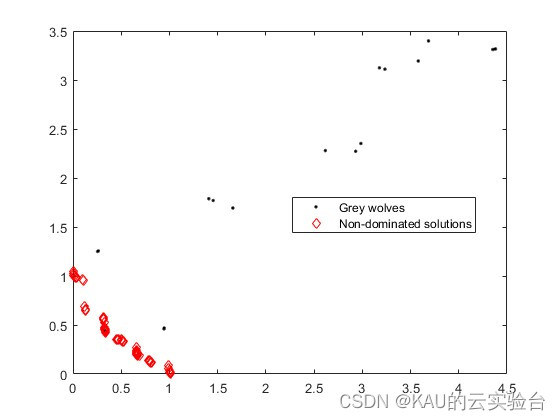
采用CEC2009的多目标测试函数集来检验其寻优性能，取UF1：

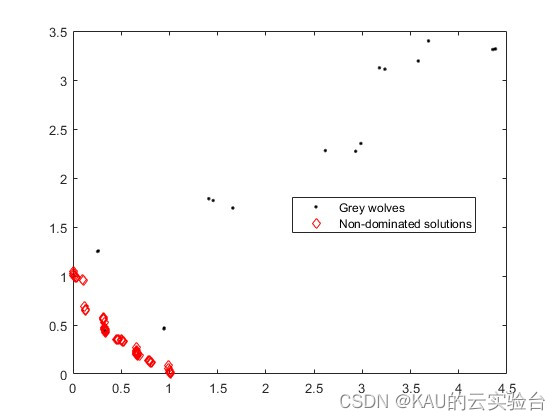
05 源码获取

GZH(KAU的云实验台)后台回复?：MOGWO

作者也将在后面的文章中更新对于多目标灰狼算法的改进，欢迎关注~

参考文献

[1] Goldberg D E, Genetic algorithms for search, optimization, and machince learning[ M]. Reading; MA: Addison-Wesley，1989: 100-150

[2] Mirjalili S,Mirjalili S M .Lewis A. Multi-objective grey wolf optimizer : A novel algorithm for multi-criterion optimization[J]. Expert Systems with Applications.2016,47:106-119

[3] C. A. C. Coello, G. T. Pulido and M. S. Lechuga, “Handling multiple objectives with particle swarm optimization,” in IEEE Transactions on Evolutionary Computation, vol. 8, no. 3, pp. 256-279, June 2004, doi: 10.1109/TEVC.2004.826067.

另：如果有伙伴有待解决的优化问题（各种领域都可），可以发我，我会选择性的更新利用优化算法解决这些问题的文章。

如果这篇文章对你有帮助或启发，可以点击右下角的赞/在看 (???_??)?(不点也行)