[足式机器人]Part2 Dr. CAN学习笔记 - Ch03 傅里叶级数与变换
本文仅供学习使用
本文参考：
B站：DR_CAN
Dr. CAN学习笔记-Ch03 傅里叶级数与变换
1. 三角函数的正交性
三角函数系 ： 集合
{
sin
?
n
x
,
cos
?
n
x
}
n
=
0
,
1
,
2
,
?
\left\{ \sin nx,\cos nx \right\} n=0,1,2,\cdots
{sinnx,cosnx}n=0,1,2,?
正交：
∫
?
π
π
sin
?
n
x
sin
?
m
x
d
x
=
0
,
n
≠
m
∫
?
π
π
sin
?
n
x
cos
?
m
x
d
x
=
0
,
n
≠
m
∫
?
π
π
cos
?
n
x
sin
?
m
x
d
x
=
0
,
n
≠
m
\int_{-\pi}^{\pi}{\sin nx\sin mx}\mathrm{d}x=0,n\ne m \\ \int_{-\pi}^{\pi}{\sin nx\cos mx}\mathrm{d}x=0,n\ne m \\ \int_{-\pi}^{\pi}{\cos nx\sin mx}\mathrm{d}x=0,n\ne m
∫?ππ?sinnxsinmxdx=0,n=m∫?ππ?sinnxcosmxdx=0,n=m∫?ππ?cosnxsinmxdx=0,n=m
积化和差：
?
∫
?
π
π
1
2
[
cos
?
(
n
?
m
)
x
+
cos
?
(
n
+
m
)
x
]
d
x
=
1
2
1
(
n
?
m
)
sin
?
(
n
?
m
)
x
∣
?
π
π
+
1
2
1
(
n
+
m
)
sin
?
(
n
+
m
)
x
∣
?
π
π
\Rightarrow \int_{-\pi}^{\pi}{\frac{1}{2}\left[ \cos \left( n-m \right) x+\cos \left( n+m \right) x \right]}\mathrm{d}x=\frac{1}{2}\frac{1}{\left( n-m \right)}\sin \left( n-m \right) x\mid_{-\pi}^{\pi}+\frac{1}{2}\frac{1}{\left( n+m \right)}\sin \left( n+m \right) x\mid_{-\pi}^{\pi}
?∫?ππ?21?[cos(n?m)x+cos(n+m)x]dx=21?(n?m)1?sin(n?m)x∣?ππ?+21?(n+m)1?sin(n+m)x∣?ππ?
∫
?
π
π
cos
?
m
x
cos
?
m
x
d
x
=
π
\int_{-\pi}^{\pi}{\cos mx\cos mx}\mathrm{d}x=\pi
∫?ππ?cosmxcosmxdx=π
2. 周期为 2 π 2\pi 2π的函数展开为傅里叶级数
T = 2 π : f ( x ) = f ( x + 2 π ) T=2\pi :f\left( x \right) =f\left( x+2\pi \right) T=2π:f(x)=f(x+2π)
f ( x ) = ∑ n = 0 ∞ a n cos ? n x + ∑ n = 0 ∞ b n sin ? n x = a 0 cos ? o x + ∑ n = 1 ∞ a n cos ? n x + b 0 sin ? 0 x + ∑ n = 1 ∞ b n sin ? n x = a 0 + ∑ n = 1 ∞ a n cos ? n x + ∑ n = 1 ∞ b n sin ? n x f\left( x \right) =\sum_{n=0}^{\infty}{a_{\mathrm{n}}\cos nx}+\sum_{n=0}^{\infty}{b_{\mathrm{n}}\sin nx}=a_0\cos ox+\sum_{n=1}^{\infty}{a_{\mathrm{n}}\cos nx}+b_0\sin 0x+\sum_{n=1}^{\infty}{b_{\mathrm{n}}\sin nx}=a_0+\sum_{n=1}^{\infty}{a_{\mathrm{n}}\cos nx}+\sum_{n=1}^{\infty}{b_{\mathrm{n}}\sin nx} f(x)=n=0∑∞?an?cosnx+n=0∑∞?bn?sinnx=a0?cosox+n=1∑∞?an?cosnx+b0?sin0x+n=1∑∞?bn?sinnx=a0?+n=1∑∞?an?cosnx+n=1∑∞?bn?sinnx
- 找
a
0
a_0
a0?:
∫ ? π π f ( x ) d x = ∫ ? π π a 0 d x + ∫ ? π π 1 ? ∑ n = 1 ∞ a n cos ? n x d x + ∫ ? π π 1 ? ∑ n = 1 ∞ b n sin ? n x d x = a 0 ∫ ? π π d x + 0 + 0 = a 0 ? 2 π \int_{-\pi}^{\pi}{f\left( x \right)}\mathrm{d}x=\int_{-\pi}^{\pi}{a_0}\mathrm{d}x+\int_{-\pi}^{\pi}{1\cdot \sum_{n=1}^{\infty}{a_{\mathrm{n}}\cos nx}}\mathrm{d}x+\int_{-\pi}^{\pi}{1\cdot \sum_{n=1}^{\infty}{b_{\mathrm{n}}\sin nx}}\mathrm{d}x \\ =a_0\int_{-\pi}^{\pi}{}\mathrm{d}x+0+0=a_0\cdot 2\pi ∫?ππ?f(x)dx=∫?ππ?a0?dx+∫?ππ?1?n=1∑∞?an?cosnxdx+∫?ππ?1?n=1∑∞?bn?sinnxdx=a0?∫?ππ?dx+0+0=a0??2π
? a 0 = 1 2 π ∫ ? π π f ( x ) d x \Rightarrow a_0=\frac{1}{2\pi}\int_{-\pi}^{\pi}{f\left( x \right)}\mathrm{d}x ?a0?=2π1?∫?ππ?f(x)dx - 找
a
n
a_n
an?:
∫ ? π π f ( x ) cos ? m x d x = ∫ ? π π a 0 cos ? m x ? 1 d x + ∫ ? π π ∑ n = 1 ∞ a n cos ? n x cos ? m x d x + ∫ ? π π ∑ n = 1 ∞ b n sin ? n x cos ? m x d x = ∫ ? π π a n cos ? n x cos ? n x d x = a n π \int_{-\pi}^{\pi}{f\left( x \right) \cos mx}\mathrm{d}x=\int_{-\pi}^{\pi}{a_0}\cos mx\cdot 1\mathrm{d}x+\int_{-\pi}^{\pi}{\sum_{n=1}^{\infty}{a_{\mathrm{n}}\cos nx\cos mx}}\mathrm{d}x+\int_{-\pi}^{\pi}{\sum_{n=1}^{\infty}{b_{\mathrm{n}}\sin nx\cos mx}}\mathrm{d}x=\int_{-\pi}^{\pi}{a_{\mathrm{n}}\cos nx\cos nx}\mathrm{d}x=a_{\mathrm{n}}\pi ∫?ππ?f(x)cosmxdx=∫?ππ?a0?cosmx?1dx+∫?ππ?n=1∑∞?an?cosnxcosmxdx+∫?ππ?n=1∑∞?bn?sinnxcosmxdx=∫?ππ?an?cosnxcosnxdx=an?π
? a n = 1 π ∫ ? π π f ( x ) cos ? n x d x \Rightarrow a_{\mathrm{n}}=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \cos nx}\mathrm{d}x ?an?=π1?∫?ππ?f(x)cosnxdx - 找
b
n
b_n
bn?:
∫ ? π π f ( x ) sin ? . m x d x ? b n = 1 π ∫ ? π π f ( x ) sin ? n x d x \int_{-\pi}^{\pi}{f\left( x \right) \sin .mx}\mathrm{d}x\Rightarrow b_{\mathrm{n}}=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \sin nx}\mathrm{d}x ∫?ππ?f(x)sin.mxdx?bn?=π1?∫?ππ?f(x)sinnxdx
? f ( x ) = f ( x + 2 π ) , T = 2 π { f ( x ) = a 0 2 + ∑ n = 0 ∞ a n cos ? n x + ∑ n = 0 ∞ b n sin ? n x a 0 = 1 2 π ∫ ? π π f ( x ) d x a n = 1 π ∫ ? π π f ( x ) cos ? n x d x b n = 1 π ∫ ? π π f ( x ) sin ? n x d x \Rightarrow f\left( x \right) =f\left( x+2\pi \right) ,T=2\pi \begin{cases} f\left( x \right) =\frac{a_0}{2}+\sum_{n=0}^{\infty}{a_{\mathrm{n}}\cos nx}+\sum_{n=0}^{\infty}{b_{\mathrm{n}}\sin nx}\\ a_0=\frac{1}{2\pi}\int_{-\pi}^{\pi}{f\left( x \right)}\mathrm{d}x\\ a_{\mathrm{n}}=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \cos nx}\mathrm{d}x\\ b_{\mathrm{n}}=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \sin nx}\mathrm{d}x\\ \end{cases} ?f(x)=f(x+2π),T=2π? ? ??f(x)=2a0??+∑n=0∞?an?cosnx+∑n=0∞?bn?sinnxa0?=2π1?∫?ππ?f(x)dxan?=π1?∫?ππ?f(x)cosnxdxbn?=π1?∫?ππ?f(x)sinnxdx?
3. 周期为 2 L 2L 2L的函数展开
f
(
t
)
=
f
(
t
+
2
L
)
f\left( t \right) =f\left( t+2L \right)
f(t)=f(t+2L) , 换元：
x
=
π
L
t
,
t
=
L
π
x
x=\frac{\pi}{L}t,t=\frac{L}{\pi}x
x=Lπ?t,t=πL?x
f
(
t
)
=
f
(
L
π
x
)
=
g
(
x
)
,
g
(
x
+
2
π
)
=
f
(
L
π
(
x
+
2
π
)
)
=
f
(
L
π
x
+
2
L
)
=
f
(
L
π
x
)
=
g
(
x
)
f\left( t \right) =f\left( \frac{L}{\pi}x \right) =g\left( x \right) ,g\left( x+2\pi \right) =f\left( \frac{L}{\pi}\left( x+2\pi \right) \right) =f\left( \frac{L}{\pi}x+2L \right) =f\left( \frac{L}{\pi}x \right) =g\left( x \right)
f(t)=f(πL?x)=g(x),g(x+2π)=f(πL?(x+2π))=f(πL?x+2L)=f(πL?x)=g(x)
g ( x ) = a 0 2 + ∑ n = 1 ∞ [ a n cos ? n x + b n sin ? n x ] a 0 = 1 2 π ∫ ? π π f ( x ) d x , a n = 1 π ∫ ? π π f ( x ) cos ? n x d x , b n = 1 π ∫ ? π π f ( x ) sin ? n x d x g\left( x \right) =\frac{a_0}{2}+\sum_{n=1}^{\infty}{\left[ a_{\mathrm{n}}\cos nx+b_{\mathrm{n}}\sin nx \right]} \\ a_0=\frac{1}{2\pi}\int_{-\pi}^{\pi}{f\left( x \right)}\mathrm{d}x,a_{\mathrm{n}}=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \cos nx}\mathrm{d}x,b_{\mathrm{n}}=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \sin nx}\mathrm{d}x g(x)=2a0??+n=1∑∞?[an?cosnx+bn?sinnx]a0?=2π1?∫?ππ?f(x)dx,an?=π1?∫?ππ?f(x)cosnxdx,bn?=π1?∫?ππ?f(x)sinnxdx
→ x = π L t ? cos ? n x = cos ? n π L t , sin ? n x = sin ? n π L t , g ( x ) = f ( t ) ∫ ? π π d x = ∫ ? π π d π L t ? 1 π ∫ ? π π d x = 1 L ∫ ? L L d t \rightarrow x=\frac{\pi}{L}t\Rightarrow \cos nx=\cos \frac{n\pi}{L}t,\sin nx=\sin \frac{n\pi}{L}t,g\left( x \right) =f\left( t \right) \\ \int_{-\pi}^{\pi}{}\mathrm{d}x=\int_{-\pi}^{\pi}{}\mathrm{d}\frac{\pi}{L}t\Rightarrow \frac{1}{\pi}\int_{-\pi}^{\pi}{}\mathrm{d}x=\frac{1}{L}\int_{-L}^L{}\mathrm{d}t →x=Lπ?t?cosnx=cosLnπ?t,sinnx=sinLnπ?t,g(x)=f(t)∫?ππ?dx=∫?ππ?dLπ?t?π1?∫?ππ?dx=L1?∫?LL?dt
?
f
(
t
)
=
a
0
2
+
∑
n
=
1
∞
[
a
n
cos
?
n
π
L
t
+
b
n
sin
?
n
π
L
t
]
,
a
0
=
1
L
∫
?
L
L
f
(
t
)
d
t
,
a
n
=
1
L
∫
?
L
L
f
(
t
)
cos
?
n
π
L
t
d
t
,
b
n
=
1
L
∫
?
L
L
f
(
t
)
sin
?
n
π
L
t
d
t
\Rightarrow f\left( t \right) =\frac{a_0}{2}+\sum_{n=1}^{\infty}{\left[ a_{\mathrm{n}}\cos \frac{n\pi}{L}t+b_{\mathrm{n}}\sin \frac{n\pi}{L}t \right]},a_0=\frac{1}{L}\int_{-L}^L{f\left( t \right)}\mathrm{d}t,a_{\mathrm{n}}=\frac{1}{L}\int_{-L}^L{f\left( t \right)}\cos \frac{n\pi}{L}t\mathrm{d}t,b_{\mathrm{n}}=\frac{1}{L}\int_{-L}^L{f\left( t \right)}\sin \frac{n\pi}{L}t\mathrm{d}t
?f(t)=2a0??+n=1∑∞?[an?cosLnπ?t+bn?sinLnπ?t],a0?=L1?∫?LL?f(t)dt,an?=L1?∫?LL?f(t)cosLnπ?tdt,bn?=L1?∫?LL?f(t)sinLnπ?tdt
4. 傅里叶级数的复数形式
f ( t ) = a 0 2 + ∑ n = 1 ∞ [ a n 1 2 ( e i n w t + e ? i n w t ) ? b n 1 2 ( e i n w t ? e ? i n w t ) ] = a 0 2 + ∑ n = 1 ∞ [ a n ? i b n 2 e i n w t + a n + i b n 2 e ? i n w t ] = ∑ n = 0 0 a 0 2 e i n w t + ∑ n = 1 ∞ a n ? i b n 2 e i n w t + ∑ n = ? ∞ ? 1 a n + i b n 2 e i n w t = ∑ n = ? ∞ ∞ C n e i n w t , C n = { a 0 2 ?? n = 0 a n ? i b n 2 ?? n = 1 , 2 , 3 , ? a n + i b n 2 ?? n = ? 1 , ? 2 , ? 3 , ? → 1 T ∫ 0 T f ( t ) d t → 1 T ∫ 0 T f ( t ) ( cos ? n w t ? i sin ? n w t ) d t = 1 T ∫ 0 T f ( t ) ( cos ? ( ? n w t ) + i sin ? ( ? n w t ) ) d t = 1 T ∫ 0 T f ( t ) e ? i n w t d t → 1 T ∫ 0 T f ( t ) e ? i n w t d t ? f ( t ) = ∑ ? ∞ ∞ C n e i n w t , C n = 1 T ∫ 0 T f ( t ) e ? i n w t d t f\left( t \right) =\frac{a_0}{2}+\sum_{n=1}^{\infty}{\left[ a_{\mathrm{n}}\frac{1}{2}\left( e^{inwt}+e^{-inwt} \right) -b_{\mathrm{n}}\frac{1}{2}\left( e^{inwt}-e^{-inwt} \right) \right]}=\frac{a_0}{2}+\sum_{n=1}^{\infty}{\left[ \frac{a_{\mathrm{n}}-ib_{\mathrm{n}}}{2}e^{inwt}+\frac{a_{\mathrm{n}}+ib_{\mathrm{n}}}{2}e^{-inwt} \right]} \\ =\sum_{n=0}^0{\frac{a_0}{2}e^{inwt}}+\sum_{n=1}^{\infty}{\frac{a_{\mathrm{n}}-ib_{\mathrm{n}}}{2}e^{inwt}}+\sum_{n=-\infty}^{-1}{\frac{a_{\mathrm{n}}+ib_{\mathrm{n}}}{2}e^{inwt}} \\ =\sum_{n=-\infty}^{\infty}{C_{\mathrm{n}}e^{inwt}},C_{\mathrm{n}}=\begin{cases} \frac{a_0}{2}\,\,n=0\\ \frac{a_{\mathrm{n}}-ib_{\mathrm{n}}}{2}\,\,n=1,2,3,\cdots\\ \frac{a_{\mathrm{n}}+ib_{\mathrm{n}}}{2}\,\,n=-1,-2,-3,\cdots\\ \end{cases}\begin{array}{c} \rightarrow \frac{1}{T}\int_0^T{f\left( t \right)}\mathrm{d}t\\ \rightarrow \frac{1}{T}\int_0^T{f\left( t \right)}\left( \cos nwt-i\sin nwt \right) \mathrm{d}t=\frac{1}{T}\int_0^T{f\left( t \right)}\left( \cos \left( -nwt \right) +i\sin \left( -nwt \right) \right) \mathrm{d}t=\frac{1}{T}\int_0^T{f\left( t \right)}e^{-inwt}\mathrm{d}t\\ \rightarrow \frac{1}{T}\int_0^T{f\left( t \right) e^{-inwt}}\mathrm{d}t\\ \end{array} \\ \Rightarrow f\left( t \right) =\sum_{-\infty}^{\infty}{C_{\mathrm{n}}e^{inwt}},C_{\mathrm{n}}=\frac{1}{T}\int_0^T{f\left( t \right) e^{-inwt}}\mathrm{d}t f(t)=2a0??+n=1∑∞?[an?21?(einwt+e?inwt)?bn?21?(einwt?e?inwt)]=2a0??+n=1∑∞?[2an??ibn??einwt+2an?+ibn??e?inwt]=n=0∑0?2a0??einwt+n=1∑∞?2an??ibn??einwt+n=?∞∑?1?2an?+ibn??einwt=n=?∞∑∞?Cn?einwt,Cn?=? ? ??2a0??n=02an??ibn??n=1,2,3,?2an?+ibn??n=?1,?2,?3,??→T1?∫0T?f(t)dt→T1?∫0T?f(t)(cosnwt?isinnwt)dt=T1?∫0T?f(t)(cos(?nwt)+isin(?nwt))dt=T1?∫0T?f(t)e?inwtdt→T1?∫0T?f(t)e?inwtdt??f(t)=?∞∑∞?Cn?einwt,Cn?=T1?∫0T?f(t)e?inwtdt
- Euler’s Formula
5. 从傅里叶级数推导傅里叶变换FT
f
T
(
t
)
=
f
(
t
+
T
)
f_{\mathrm{T}}\left( t \right) =f\left( t+T \right)
fT?(t)=f(t+T)
f
T
(
t
)
=
∑
?
∞
∞
C
n
e
i
n
w
0
t
f_{\mathrm{T}}\left( t \right) =\sum_{-\infty}^{\infty}{C_{\mathrm{n}}e^{inw_0t}}
fT?(t)=∑?∞∞?Cn?einw0?t, 基频率：
w
0
=
2
π
T
w_0=\frac{2\pi}{T}
w0?=T2π?, 定义函数:
C
n
=
1
T
∫
?
T
2
T
2
f
T
(
t
)
e
?
i
n
w
t
d
t
C_{\mathrm{n}}=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f_{\mathrm{T}}\left( t \right) e^{-inwt}}\mathrm{d}t
Cn?=T1?∫?2T?2T??fT?(t)e?inwtdt
非周期，一般形式：
T
→
∞
T\rightarrow \infty
T→∞
lim
?
T
→
∞
f
T
(
t
)
=
f
(
t
)
,
Δ
w
=
(
n
+
1
)
w
0
?
n
w
0
=
w
0
=
2
π
T
??
T
↗
Δ
w
↘
\underset{T\rightarrow \infty}{\lim}f_{\mathrm{T}}\left( t \right) =f\left( t \right) ,\varDelta w=\left( n+1 \right) w_0-nw_0=w_0=\frac{2\pi}{T}\,\,T\nearrow \varDelta w\searrow
T→∞lim?fT?(t)=f(t),Δw=(n+1)w0??nw0?=w0?=T2π?T↗Δw↘
f T ( t ) = ∑ ? ∞ ∞ ( 1 T ∫ ? T 2 T 2 f T ( t ) e ? i n w 0 t d t ) e i n w 0 t , 1 T = Δ w 2 π ? f T ( t ) = ∑ ? ∞ ∞ ( Δ w 2 π ∫ ? T 2 T 2 f T ( t ) e ? i n w 0 t d t ) e i n w 0 t , T → ∞ : { ∫ ? T 2 T 2 d t → ∫ ? ∞ ∞ d t n w 0 → w ∑ ? ∞ ∞ Δ w → ∫ ? ∞ ∞ d w ? f ( t ) = 1 2 π ∫ ? ∞ ∞ ( ∫ ? ∞ ∞ f ( t ) e ? i w t d t ) e i w t d w , ∫ ? ∞ ∞ f ( t ) e ? i w t d t = F ( w ) ? f ( t ) = 1 2 π ∫ ? ∞ ∞ F ( w ) e i w t d w f_{\mathrm{T}}\left( t \right) =\sum_{-\infty}^{\infty}{\left( \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f_{\mathrm{T}}\left( t \right) e^{-inw_0t}}\mathrm{d}t \right) e^{inw_0t}},\frac{1}{T}=\frac{\varDelta w}{2\pi} \\ \Rightarrow f_{\mathrm{T}}\left( t \right) =\sum_{-\infty}^{\infty}{\left( \frac{\varDelta w}{2\pi}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f_{\mathrm{T}}\left( t \right) e^{-inw_0t}}\mathrm{d}t \right) e^{inw_0t}},T\rightarrow \infty :\begin{cases} \int_{-\frac{T}{2}}^{\frac{T}{2}}{}\mathrm{d}t\rightarrow \int_{-\infty}^{\infty}{}\mathrm{d}t\\ nw_0\rightarrow w\\ \sum_{-\infty}^{\infty}{\varDelta w}\rightarrow \int_{-\infty}^{\infty}{}\mathrm{d}w\\ \end{cases} \\ \Rightarrow f\left( t \right) =\frac{1}{2\pi}\int_{-\infty}^{\infty}{\left( \int_{-\infty}^{\infty}{f\left( t \right) e^{-iwt}}\mathrm{d}t \right)}e^{iwt}\mathrm{d}w,\int_{-\infty}^{\infty}{f\left( t \right) e^{-iwt}}\mathrm{d}t=F\left( w \right) \\ \Rightarrow f\left( t \right) =\frac{1}{2\pi}\int_{-\infty}^{\infty}{F\left( w \right)}e^{iwt}\mathrm{d}w fT?(t)=?∞∑∞?(T1?∫?2T?2T??fT?(t)e?inw0?tdt)einw0?t,T1?=2πΔw??fT?(t)=?∞∑∞?(2πΔw?∫?2T?2T??fT?(t)e?inw0?tdt)einw0?t,T→∞:? ? ??∫?2T?2T??dt→∫?∞∞?dtnw0?→w∑?∞∞?Δw→∫?∞∞?dw??f(t)=2π1?∫?∞∞?(∫?∞∞?f(t)e?iwtdt)eiwtdw,∫?∞∞?f(t)e?iwtdt=F(w)?f(t)=2π1?∫?∞∞?F(w)eiwtdw
F ( w ) = ∫ ? ∞ ∞ f ( t ) e ? i w t d t F\left( w \right) =\int_{-\infty}^{\infty}{f\left( t \right) e^{-iwt}}\mathrm{d}t F(w)=∫?∞∞?f(t)e?iwtdt : FT 傅里叶变换
f ( t ) = 1 2 π ∫ ? ∞ ∞ F ( w ) e i w t d w f\left( t \right) =\frac{1}{2\pi}\int_{-\infty}^{\infty}{F\left( w \right)}e^{iwt}\mathrm{d}w f(t)=2π1?∫?∞∞?F(w)eiwtdw : 逆变换
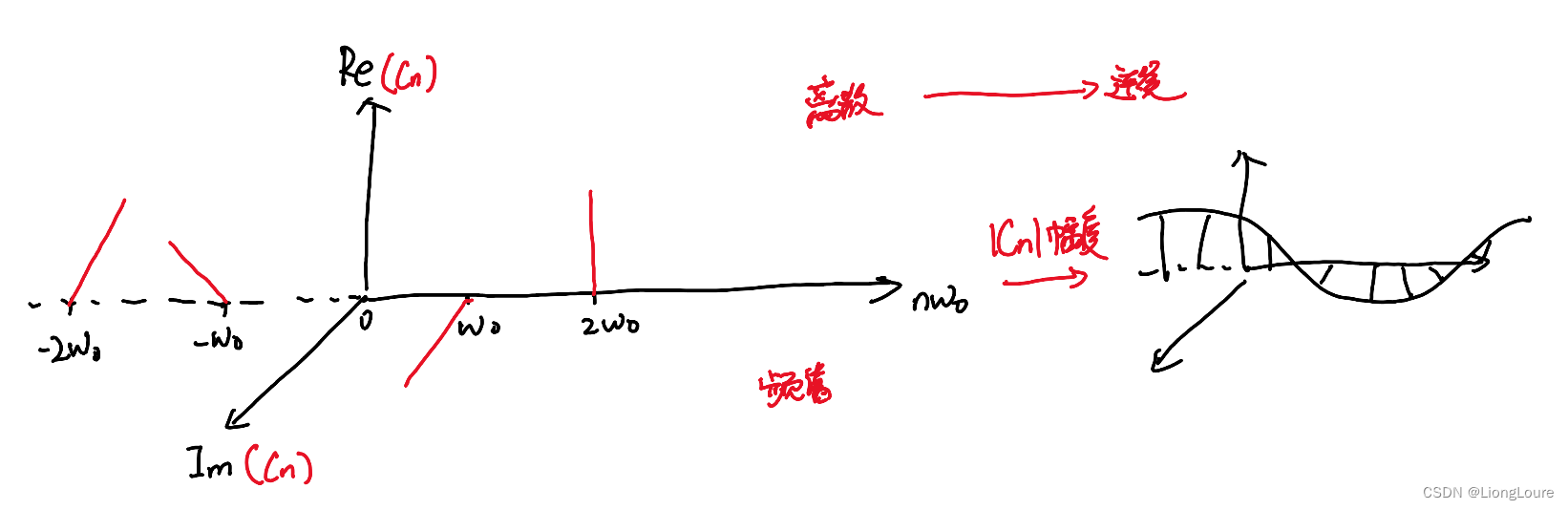
6. 总结
三角函数的正交性：
[
0
,
1
,
sin
?
x
,
cos
?
x
,
sin
?
2
x
,
cos
?
2
x
,
?
?
,
sin
?
n
x
,
cos
?
n
x
]
,
n
=
0
,
1
,
2
,
?
\left[ 0,1,\sin x,\cos x,\sin 2x,\cos 2x,\cdots ,\sin nx,\cos nx \right] ,n=0,1,2,\cdots
[0,1,sinx,cosx,sin2x,cos2x,?,sinnx,cosnx],n=0,1,2,?
∫
?
π
π
sin
?
n
x
sin
?
m
x
d
x
=
0
,
n
≠
m
∫
?
π
π
sin
?
n
x
sin
?
m
x
d
x
=
0
,
n
≠
m
∫
?
π
π
sin
?
n
x
cos
?
m
x
d
x
=
0
,
n
≠
m
\int_{-\pi}^{\pi}{\sin nx\sin mx}\mathrm{d}x=0,n\ne m \\ \int_{-\pi}^{\pi}{\sin nx\sin mx}\mathrm{d}x=0,n\ne m \\ \int_{-\pi}^{\pi}{\sin nx\cos mx}\mathrm{d}x=0,n\ne m
∫?ππ?sinnxsinmxdx=0,n=m∫?ππ?sinnxsinmxdx=0,n=m∫?ππ?sinnxcosmxdx=0,n=m
周期
2
π
2\pi
2π :
f
(
x
)
=
f
(
x
+
2
π
)
f\left( x \right) =f\left( x+2\pi \right)
f(x)=f(x+2π)
f
(
x
)
=
∑
n
=
0
∞
a
n
cos
?
n
x
+
∑
n
=
0
∞
b
n
sin
?
n
x
←
f
(
x
)
=
a
0
2
+
∑
n
=
0
∞
a
n
cos
?
n
x
+
∑
n
=
0
∞
b
n
sin
?
n
x
f\left( x \right) =\sum_{n=0}^{\infty}{a_{\mathrm{n}}\cos nx}+\sum_{n=0}^{\infty}{b_{\mathrm{n}}\sin nx}\gets f\left( x \right) =\frac{a_0}{2}+\sum_{n=0}^{\infty}{a_{\mathrm{n}}\cos nx}+\sum_{n=0}^{\infty}{b_{\mathrm{n}}\sin nx}
f(x)=n=0∑∞?an?cosnx+n=0∑∞?bn?sinnx←f(x)=2a0??+n=0∑∞?an?cosnx+n=0∑∞?bn?sinnx
a
0
=
1
2
π
∫
?
π
π
f
(
x
)
d
x
,
a
n
=
1
π
∫
?
π
π
f
(
x
)
cos
?
n
x
d
x
,
b
n
=
1
π
∫
?
π
π
f
(
x
)
sin
?
n
x
d
x
a_0=\frac{1}{2\pi}\int_{-\pi}^{\pi}{f\left( x \right)}\mathrm{d}x,a_{\mathrm{n}}=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \cos nx}\mathrm{d}x,b_{\mathrm{n}}=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \sin nx}\mathrm{d}x
a0?=2π1?∫?ππ?f(x)dx,an?=π1?∫?ππ?f(x)cosnxdx,bn?=π1?∫?ππ?f(x)sinnxdx
周期
2
L
2L
2L :
T
=
2
L
,
f
(
t
)
=
f
(
t
+
2
L
)
,
x
=
π
L
t
T=2L,f\left( t \right) =f\left( t+2L \right) ,x=\frac{\pi}{L}t
T=2L,f(t)=f(t+2L),x=Lπ?t
f
(
t
)
=
a
0
2
+
∑
n
=
1
∞
[
a
n
cos
?
n
π
L
t
+
b
n
sin
?
n
π
L
t
]
f\left( t \right) =\frac{a_0}{2}+\sum_{n=1}^{\infty}{\left[ a_{\mathrm{n}}\cos \frac{n\pi}{L}t+b_{\mathrm{n}}\sin \frac{n\pi}{L}t \right]}
f(t)=2a0??+n=1∑∞?[an?cosLnπ?t+bn?sinLnπ?t]
a
0
=
1
L
∫
?
L
L
f
(
t
)
d
t
,
a
n
=
1
L
∫
?
L
L
f
(
t
)
cos
?
n
π
L
t
d
t
,
b
n
=
1
L
∫
?
L
L
f
(
t
)
sin
?
n
π
L
t
d
t
a_0=\frac{1}{L}\int_{-L}^L{f\left( t \right)}\mathrm{d}t,a_{\mathrm{n}}=\frac{1}{L}\int_{-L}^L{f\left( t \right)}\cos \frac{n\pi}{L}t\mathrm{d}t,b_{\mathrm{n}}=\frac{1}{L}\int_{-L}^L{f\left( t \right)}\sin \frac{n\pi}{L}t\mathrm{d}t
a0?=L1?∫?LL?f(t)dt,an?=L1?∫?LL?f(t)cosLnπ?tdt,bn?=L1?∫?LL?f(t)sinLnπ?tdt
复指数：
f
(
t
)
=
∑
?
∞
∞
C
n
e
i
n
w
0
t
,
w
0
=
2
π
T
,
C
n
=
1
T
∫
0
T
f
(
t
)
e
?
i
n
w
0
t
d
t
f\left( t \right) =\sum_{-\infty}^{\infty}{C_{\mathrm{n}}e^{inw_0t}},w_0=\frac{2\pi}{T},C_{\mathrm{n}}=\frac{1}{T}\int_0^T{f\left( t \right) e^{-inw_0t}}\mathrm{d}t
f(t)=?∞∑∞?Cn?einw0?t,w0?=T2π?,Cn?=T1?∫0T?f(t)e?inw0?tdt
FT ：
f
(
t
)
=
f
(
t
+
T
)
,
T
→
∞
f\left( t \right) =f\left( t+T \right) ,T\rightarrow \infty
f(t)=f(t+T),T→∞ ,
f
(
t
)
=
1
2
π
∫
?
∞
∞
(
∫
?
∞
∞
f
(
t
)
e
?
i
w
t
d
t
)
e
i
w
t
d
w
f\left( t \right) =\frac{1}{2\pi}\int_{-\infty}^{\infty}{\left( \int_{-\infty}^{\infty}{f\left( t \right) e^{-iwt}}\mathrm{d}t \right)}e^{iwt}\mathrm{d}w
f(t)=2π1?∫?∞∞?(∫?∞∞?f(t)e?iwtdt)eiwtdw
F
T
→
F
(
w
)
=
∫
?
∞
∞
f
(
t
)
e
?
i
w
t
d
t
I
F
T
→
(
t
)
=
1
2
π
∫
?
∞
∞
F
(
w
)
e
i
w
t
d
w
\begin{array}{c} FT\rightarrow F\left( w \right) =\int_{-\infty}^{\infty}{f\left( t \right) e^{-iwt}}\mathrm{d}t\\ IFT\rightarrow \left( t \right) =\frac{1}{2\pi}\int_{-\infty}^{\infty}{F\left( w \right)}e^{iwt}\mathrm{d}w\\ \end{array}
FT→F(w)=∫?∞∞?f(t)e?iwtdtIFT→(t)=2π1?∫?∞∞?F(w)eiwtdw?
Laplace :
F
(
s
)
:
∫
?
∞
∞
f
(
t
)
e
?
s
t
d
t
F\left( s \right) :\int_{-\infty}^{\infty}{f\left( t \right) e^{-st}}\mathrm{d}t
F(s):∫?∞∞?f(t)e?stdt
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！