算法训练day56｜动态规划part16

583. 两个字符串的删除操作

逆向思路：求最长公共子序列，在用总长度-2*公共子序列长度

正向思路：删除多少

1.?dp数组（dp table）以及下标的含义

dp[i][j]：以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，想要达到相等，所需要删除元素的最少次数

2. 递推公式

• 当word1[i - 1] 与 word2[j - 1]相同的时候
• 当word1[i - 1] 与 word2[j - 1]不相同的时候

当word1[i - 1] 与 word2[j - 1]相同的时候，dp[i][j] = dp[i - 1][j - 1];

当word1[i - 1] 与 word2[j - 1]不相同的时候，有三种情况：

情况一：删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1

情况二：删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1

情况三：同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2

递推公式可简化为：dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);

当 同时删word1[i - 1]和word2[j - 1]，dp[i][j-1] 本来就不考虑 word2[j - 1]了，那么我在删 word1[i - 1]，是不是就达到两个元素都删除的效果，即 dp[i][j-1] + 1

4. 遍历顺序

?dp[i][j] = min(dp[i - 1][j - 1] + 2, min(dp[i - 1][j], dp[i][j - 1]) + 1); 和dp[i][j] = dp[i - 1][j - 1]可以看出dp[i][j]都是根据左上方、正上方、正左方推出来的。

所以遍历的时候一定是从上到下，从左到右，这样保证dp[i][j]可以根据之前计算出来的数值进行计算

// dp数组中存储需要删除的字符个数
class Solution {
    public int minDistance(String word1, String word2) {
        int[][] dp = new int[word1.length() + 1][word2.length() + 1];
        for (int i = 0; i < word1.length() + 1; i++) dp[i][0] = i;
        for (int j = 0; j < word2.length() + 1; j++) dp[0][j] = j;
        
        for (int i = 1; i < word1.length() + 1; i++) {
            for (int j = 1; j < word2.length() + 1; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                }else{
                    dp[i][j] = Math.min(dp[i - 1][j - 1] + 2,
                                        Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));
                }
            }
        }
        
        return dp[word1.length()][word2.length()];
    }
}

72. 编辑距离

与之前题目重点区别是：递推公式：有三种改法

重点思路：最后两个相同，并不是某一个一定要变成另一个，所以增加和删减其实是相同的。长的变短其实就是短的增加变成

dp数组（dp table）以及下标的含义

dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。

2. 递推公式：

if (word1[i - 1] == word2[j - 1])
    不操作
if (word1[i - 1] != word2[j - 1])
    增
    删
    换

if (word1[i - 1] == word2[j - 1])?那么说明不用任何编辑，dp[i][j]?就应该是?dp[i - 1][j - 1]，即dp[i][j] = dp[i - 1][j - 1];

word1[i - 1]?与?word2[j - 1]相等了，那么就不用编辑了，以下标i-2为结尾的字符串word1和以下标j-2为结尾的字符串word2的最近编辑距离dp[i - 1][j - 1]就是?dp[i][j]了。

if (word1[i - 1] != word2[j - 1])，此时就需要编辑了

• 操作一：word1删除一个元素，那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。

即?dp[i][j] = dp[i - 1][j] + 1;

• 操作二：word2删除一个元素，那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。

即?dp[i][j] = dp[i][j - 1] + 1;

word2添加一个元素，相当于word1删除一个元素，例如?word1 = "ad" ，word2 = "a"，word1删除元素'd'?和?word2添加一个元素'd'，变成word1="a", word2="ad"， 最终的操作数是一样！ dp数组如下图所示意的：

            a                         a     d
   +-----+-----+             +-----+-----+-----+
   |  0  |  1  |             |  0  |  1  |  2  |
   +-----+-----+   ===>      +-----+-----+-----+
 a |  1  |  0  |           a |  1  |  0  |  1  |
   +-----+-----+             +-----+-----+-----+
 d |  2  |  1  |
   +-----+-----+

操作三：替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同，此时不用增删加元素。

可以回顾一下，if (word1[i - 1] == word2[j - 1])的时候我们的操作 是?dp[i][j] = dp[i - 1][j - 1]?对吧。

那么只需要一次替换的操作，就可以让 word1[i - 1] 和 word2[j - 1] 相同。

所以?dp[i][j] = dp[i - 1][j - 1] + 1;

综上，当?if (word1[i - 1] != word2[j - 1])?时取最小的，即：dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;

递归公式代码如下：

if (word1[i - 1] == word2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1];
}
else {
    dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}

3. 初始化：

那么dp[i][0] 和 dp[0][j] 表示什么呢？

dp[i][0] ：以下标i-1为结尾的字符串word1，和空字符串word2，最近编辑距离为dp[i][0]。

那么dp[i][0]就应该是i，对word1里的元素全部做删除操作，即：dp[i][0] = i;

同理dp[0][j] = j;

4.遍历顺序

• dp[i][j] = dp[i - 1][j - 1]
• dp[i][j] = dp[i - 1][j - 1] + 1
• dp[i][j] = dp[i][j - 1] + 1
• dp[i][j] = dp[i - 1][j] + 1

可以看出dp[i][j]是依赖左方，上方和左上方元素的，如图：

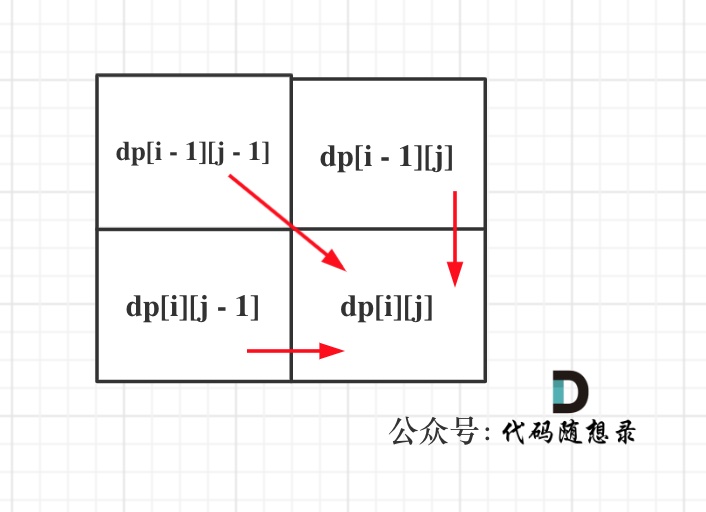
public int minDistance(String word1, String word2) {
    int m = word1.length();
    int n = word2.length();
    int[][] dp = new int[m + 1][n + 1];
    // 初始化
    for (int i = 1; i <= m; i++) {
        dp[i][0] =  i;
    }
    for (int j = 1; j <= n; j++) {
        dp[0][j] = j;
    }
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            // 因为dp数组有效位从1开始
            // 所以当前遍历到的字符串的位置为i-1 | j-1
            if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                dp[i][j] = dp[i - 1][j - 1];
            } else {
                dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1;
            }
        }
    }
    return dp[m][n];
}