Leetcode 106. 从中序与后序遍历序列构造二叉树
发布时间:2024年01月21日
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
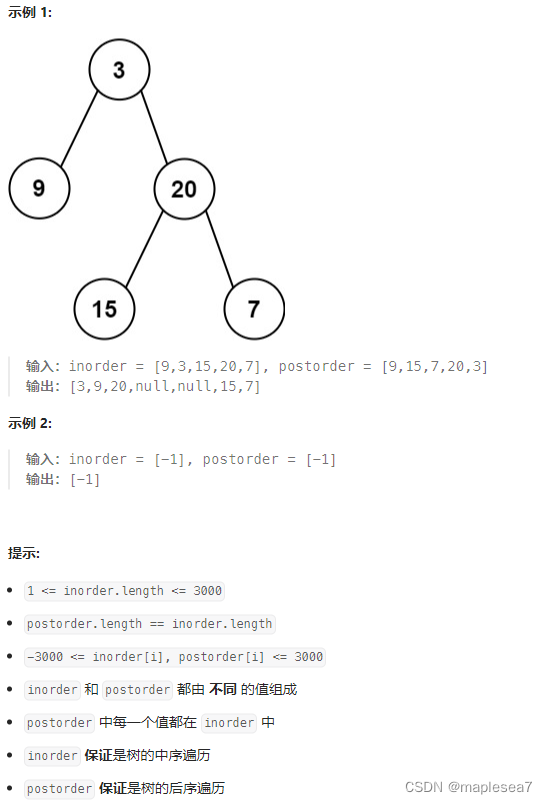
首先需要明确,怎样使用中序遍历和后序遍历来构成唯一的二叉树。
中序遍历:左根右
后序遍历:左右根
可知树的根一定是后序遍历的最后一个数。此时我们需要在中序遍历中找到这个数,即为根。以根为中心,左边是左子树,右边是右子树。
接下来的事情就可以交给递归,唯一的问题在于递归的传入参数了,即递归调用buildTree函数时,inorder和postorder又分别指数组的哪一段到哪一段。
假设当前根结点在inorder中的坐标为i,i左侧即为左子树,右侧即为右子树。用函数Arrays.copyOfRange可以对相应数组进行裁剪。
当寻找左子树时,inorder需要的坐标范围为[0, i),postorder需要的坐标范围也为[0, i);
当寻炸右子树时,inorder需要的坐标范围为[i+1, postorder.length),postorder需要的坐标范围也为[i, postorder.length-1)。
最后,当inorder和postorder中只剩下最后一个数时,说明当前子树建立完成,可以return。
实现代码如下:
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
TreeNode root = new TreeNode(postorder[postorder.length-1]);
//i用来寻找inorder中的根结点位置
int i=0;
while(inorder[i]!=postorder[postorder.length-1]) i++;
if(i>0) {//一定有左子树
root.left=buildTree(Arrays.copyOfRange(inorder, 0, i),
Arrays.copyOfRange(postorder,0,i));
}
if(i<postorder.length -1) {//一定有右子树
root.right=buildTree(Arrays.copyOfRange(inorder, i+1, postorder.length),
Arrays.copyOfRange(postorder,i,postorder.length-1));
}
//如果不满足上述两个if,就说明已经是最后一个结点了,可以返回了
return root;
}
}
文章来源:https://blog.csdn.net/ignb6666/article/details/135685085
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 大型语言模型基础知识的可视化指南
- 910b上跑Chatglm3-6b进行流式输出【pytorch框架】
- 哈希(包含闭散列和开散列实现)
- Javascript本地存储的方式有哪些?区别及应用场景?
- OSPF:08 OSPF链路状态数据库
- Flutter 监听前台和后台切换的状态
- 鸿蒙(HarmonyOS)开发学习笔记免费分享,自学必备
- 深入理解Lock Support
- js基础:函数、对象、WebAPIs-DOM
- 数据库-各种查询看着一篇就够了