CF1446C Xor Tree

题意【?here 】

分析

? ? ? ? ①看到求异或和最小时，很容易想到?trie树??再等高建完trie树后两个最接近的点就为

? ? ? ? 异或值最小的数（越低位不同，对异或值的影响越小）

? ? ? ? ②由于删数比较难计算，所以可以通过计算能保留的最大值来间接计算? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??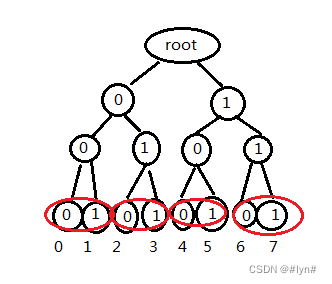

? ? ? ? ③? 因为异或值最小的两个数才会连边。 所以没删除前一定是?TrieTrie?树中如下图所示的点所表示的数会连边，不难发现他们是不连通的。要让他们变为一棵树，就必须删除一些点。

? ? ? ? ④当要处理倒数第二层以上的点时，就必须要让两棵子树的其中一棵只保留一个数字。（因为?TrieTrie?树中一个子树内任意两个数的异或值一定比一个子树内的数与一个子树外的数异或值小。）

? ? ? ? ⑤ 所以为了让这棵子树内的树与另一棵子树上的树连边，只能令这棵子树只留下它一个数。为了让它跟优，所以取个数较大的子树的个数和另一个子树中的一个作为答案

? ? ? ? ⑥ 爆搜（干就完了）

Code

? ? ? ? 注意t数组的下标要开大一点（2倍也不行），否则会?RE

#include<bits/stdc++.h>
using namespace std;
int n,tot=1,x,t[4000005][2];
void insert(int x)
{
	int p=1;
	for(int i=30;i>=0;i--)
	{
		int v=x>>i&1;
		if(!t[p][v]) t[p][v]=++tot;
		p=t[p][v];
	}
}//构造trie树
int get(int x)
{
	if(!t[x][0] && !t[x][1]) return 1;
	if(!t[x][0]) return get(t[x][1]);
	if(!t[x][1]) return get(t[x][0]);
	return max(get(t[x][0]),get(t[x][1]))+1;
}
int main()
{
 	scanf("%d",&n);
 	for(int i=1;i<=n;i++) scanf("%d",&x),insert(x);
 	cout<<n-get(1);
	return 0;
}