NLP深入学习（九）：KNN 算法及分类用法

---

0. 引言

前情提要：
《NLP深入学习（一）：jieba 工具包介绍》
《NLP深入学习（二）：nltk 工具包介绍》
《NLP深入学习（三）：TF-IDF 详解以及文本分类/聚类用法》
《NLP深入学习（四）：贝叶斯算法详解及分类/拼写检查用法》
《NLP深入学习（五）：HMM 详解及字母识别/天气预测用法》
《NLP深入学习（六）：n-gram 语言模型》
《NLP深入学习（七）：词向量》
《NLP深入学习（八）：感知机学习》

1. 什么是 KNN

K 近邻（K-Nearest Neighbors, KNN）算法是一种基础且直观的监督学习方法，用于分类和回归任务。在处理新的数据点时，KNN 算法基于“物以类聚”的原则，通过计算新样本与已有训练样本之间的距离，找出最接近的 k 个邻居，并根据这些邻居的类别或属性来预测新样本的类别或数值。

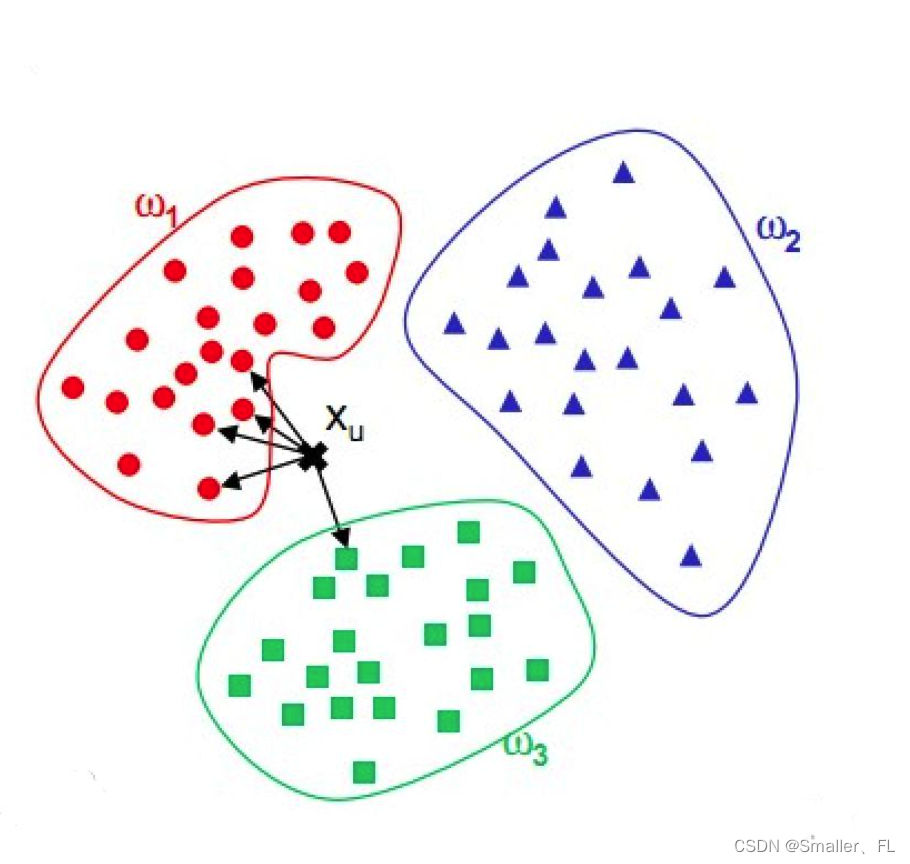
工作原理：

1. 训练阶段：

   • 在 KNN 中不存在明确的训练过程。算法仅存储整个训练集，不需要对训练数据进行任何模型拟合操作。KNN 算法的核心在于计算样本之间的距离，然后根据距离选择最近的邻居来进行分类或回归。以下是计算公式和步骤：
     • 对于欧式距离（最常用的距离度量方法），假设我们有新样本 $x_{new}$ 和训练集中的一个样本 $x_i$，它们都是 n 维向量，则两个样本之间的欧氏距离计算公式为：
       $$d(x_{new},x_i)=\sqrt{\sum _{j=1}^n(x_{new,j}?x_{i,j}{)}^2}$$
     • 其他常见的距离度量包括曼哈顿距离、切比雪夫距离、马氏距离等。

2. 找出k个最近邻：

   • 计算新样本与训练集中所有样本的距离后，按照距离从小到大排序，并选择前k个最近的样本作为“邻居”。

3. 分类决策规则（针对分类任务）：

   • 多数表决：统计这k个邻居中属于各个类别的样本数量，将新样本预测为出现次数最多的类别。
   • 加权投票：赋予每个邻居以一定的权重（通常根据其与新样本的距离来加权，距离越近权重越大），然后对各类别进行加权投票决定新样本的类别。

4. 回归预测规则（针对回归任务）：

   • 平均值法：计算这k个邻居的目标变量（连续数值）的平均值作为新样本的预测值。

2. k 值的选择

k 值的选择是 KNN 算法的关键。较小的 k 值可能导致模型过拟合，而较大的k值可能会使模型过于保守导致欠拟合。一般使用交叉验证，通过交叉验证来评估不同k值对模型性能的影响。将数据集划分为训练集和验证集（或使用k折交叉验证），针对一系列不同的k值，在训练集上计算每个样本的k个最近邻，并在验证集上评估模型性能（如分类任务中的准确率、召回率、F1分数等）。

3. kd 树

KNN 算法在高维数据上的效率可能会受到严重的影响，因为在高维空间中计算距离的开销很大。为了加速 KNN 算法在高维空间的执行，可以使用 kd 树（k-dimensional tree）这种数据结构。

kd 树是一种二叉树结构，用于组织k维空间中的数据点。它的构建和搜索过程允许更有效地找到近邻点，从而提高了 KNN 算法的性能。

3.1 构建 kd 树：

1. 选择轴： 在树的每一层，选择一个轴（特征维度）来进行划分。通常选择方差最大的轴作为划分轴。

2. 选择划分点： 在选定的轴上，选择当前数据集中的中位数作为划分点，将数据分为两个子集。

3. 递归构建： 对划分点两侧的数据集递归执行上述过程，构建子树。

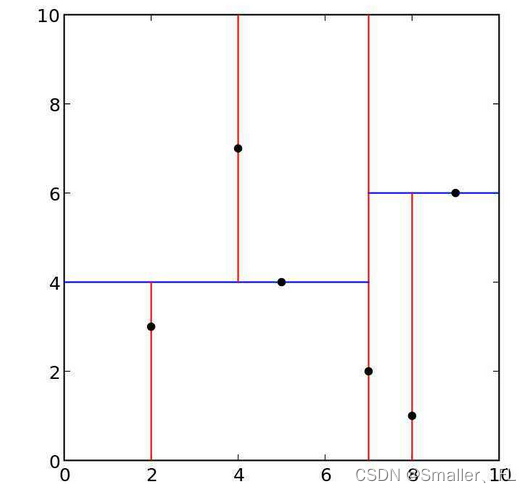
例如，上面的各个点：
（1）第一次划分，x=7，分为两部分
（2）左边的矩形划分，y=4，分为两部分；上面的用 x=4，下面用 x=2划分
（3）左边的矩形划分，y=6，也分为两部分；下面用 x=8 划分
最终，得到的 kd 树如下：

3.2 kd 树搜索：

1. 根据轴进行搜索： 从根节点开始，根据查询点在当前轴上的值比较，选择向左或向右子树移动。

2. 递归搜索： 在选择的子树上递归执行搜索。

3. 更新最近邻点： 在搜索的过程中，维护一个当前最近邻点的列表。如果发现更近的点，则更新最近邻点。

4. 回溯： 在回溯过程中，检查是否需要在另一个子树中继续搜索。

kd 树的优点是在处理高维数据时可以减少搜索的计算开销，因为它在每一步都可以剪枝。然而，kd 树的构建和搜索过程相对复杂，适用于数据集较大、查询点较多的情况。

3.3 例子

下面我将提供一个简单的 Python 代码示例，演示如何构建一个二维数据集的 kd 树以及如何使用 kd 树进行最近邻搜索。请注意，这只是一个基本示例，实际应用中可能需要考虑更多的细节和优化。

import numpy as np

class Node:
    def __init__(self, point, axis, left=None, right=None):
        self.point = point
        self.axis = axis
        self.left = left
        self.right = right

def build_kdtree(points, depth=0):
    if len(points) == 0:
        return None

    k = len(points[0])  # 维度
    axis = depth % k  # 选择轴

    # 根据轴排序并选择中位数作为划分点
    points.sort(key=lambda x: x[axis])
    median = len(points) // 2

    return Node(
        point=points[median],
        axis=axis,
        left=build_kdtree(points[:median], depth + 1),
        right=build_kdtree(points[median + 1:], depth + 1)
    )

def closest_point(root, target, depth=0, best=None):
    if root is None:
        return best

    k = len(target)
    axis = depth % k

    next_best = None
    next_branch = None

    if target[axis] < root.point[axis]:
        next_branch = root.left
    else:
        next_branch = root.right

    next_best = closest_point(next_branch, target, depth + 1, next_best)

    # 更新最近邻点
    if best is None or np.linalg.norm([target[i] - root.point[i] for i in range(k)]) < np.linalg.norm([target[i] - best[i] for i in range(k)]):
        best = root.point

    # 检查另一个分支是否可能包含更近的点
    if abs(target[axis] - root.point[axis]) < np.linalg.norm([target[i] - best[i] for i in range(k)]):
        next_branch = root.right if next_branch == root.left else root.left
        next_best = closest_point(next_branch, target, depth + 1, next_best)

    return best

# 示例数据集
data_points = [(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)]
query_point = (9,2)

# 构建kd树
kd_tree = build_kdtree(data_points)

# 查找最近邻点
nearest_neighbor = closest_point(kd_tree, query_point)

print("Data Points:", data_points)
print("Query Point:", query_point)
print("Nearest Neighbor:", nearest_neighbor)

在这个例子中，我们首先定义了一个 Node 类来表示 kd 树的节点，然后使用 build_kdtree 函数构建 kd 树。最后，使用 closest_point 函数来查找查询点的最近邻点。

4. 参考

《NLP深入学习（一）：jieba 工具包介绍》
《NLP深入学习（二）：nltk 工具包介绍》
《NLP深入学习（三）：TF-IDF 详解以及文本分类/聚类用法》
《NLP深入学习（四）：贝叶斯算法详解及分类/拼写检查用法》
《NLP深入学习（五）：HMM 详解及字母识别/天气预测用法》
《NLP深入学习（六）：n-gram 语言模型》
《NLP深入学习（七）：词向量》
《NLP深入学习（八）：感知机学习》

欢迎关注本人，我是喜欢搞事的程序猿； 一起进步，一起学习；

也欢迎关注我的wx公众号：一个比特定乾坤