前缀和和差分
发布时间:2024年01月08日
一维差分
做好前缀和之后做一次差分就可以算出来了。
a[i]=a[i-1]+a[i]
使用前面的数值求和,覆盖当前数值。
使用前缀和能够大幅度降低时间复杂度。
举个例子:
0 0 0 0 0 0 0 0?
将上面数值赋值成
0 0 1 0 0 0 0 -1
这样进行前缀和的时候就可以实现某一个区间的加和(-1会覆盖前面1加和的效果,使得后面的区间不再进行加和),最终实现特定区间的加和,同时加同一个数值。
二维差分
l[i][j]=l[i-1][j]+l[i][i-1]-l[i-1][j-1]+a[i][j]
对于二维数组进行前缀和,结合题目进行理解
题目描述
作为在虚拟世界里统帅千军万马的领袖,小 Z 认为天时、地利、人和三者是缺一不可的,所以,谨慎地选择首都的位置对于小 Z 来说是非常重要的。
首都被认为是一个占地 C×C?的正方形。小 Z 希望你寻找到一个合适的位置,使得首都所占领的位置的土地价值和最高。
输入格式
第一行三个整数?N,M,C,表示地图的宽和长以及首都的边长。
接下来 N?行每行M?个整数,表示了地图上每个地块的价值。价值可能为负数。
输出格式
一行两个整数X,Y,表示首都左上角的坐标。
输入输出样例
输入 3 4 2 1 2 3 1 -1 9 0 2 2 0 1 1输出
1 2
对应AC代码如下
#include <iostream>
#include<bits/stdc++.h>
using namespace std;
int main() {
int N,M,C;
cin>>N>>M>>C;
int X,Y=0;
int s[N+10][M+10];
memset(s,0,sizeof(s));
// int sum=0;
for (int i=1;i<=N;i++)
{
for (int j=1;j<=M;j++)
cin>>s[i][j];
}
//每个坐标数值对应左上角的数值和
int l[N+10][M+10];
memset(l,0,sizeof(l));
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++){
l[i][j]=l[i-1][j]+l[i][j-1]-l[i-1][j-1]+s[i][j];
// cout<<l[i][j]<<" \n"[j==M];
}
}
int z=-1e9;int x,y;
for(int i=1;i<=N-C+1;i++)
for(int j=1;j<=M-C+1;j++)
{
int sum1=l[i+C-1][j+C-1]-l[i+C-1][j-1]-l[i-1][j+C-1]+l[i-1][j-1];
if(sum1>z)
{
z=sum1;
x=i;
y=j;
}
}
cout<<x<<" "<<y;
// cout<<z;
return 0; }
上述代码中,我首先设立了二维数组s存储原始数据,然后重新创建了二维数组l存储前缀和,结合下图进行理解?
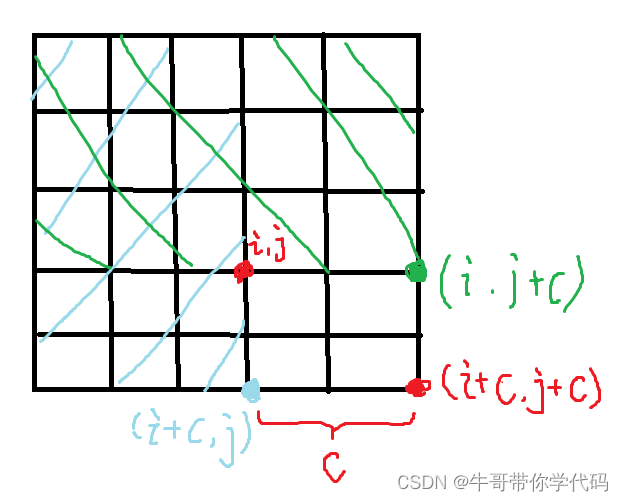
对应的i,j(领地左上角) 要留出边长为C的范围。此外,要先减去左侧矩形,再减去上面矩形,再将重复减去的矩形加上,最终得到结果。
文章来源:https://blog.csdn.net/weixin_60535956/article/details/135454713
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!