排序之快速排序
????????快速排序也许是最常用的排序算法了。它的复杂度为O(nlogn),且它的性能通常比其他的复
杂度为O(nlogn)的排序算法要好。和归并排序一样,快速排序也使用分治的方法,将原始数组分
为较小的数组(但它没有像归并排序那样将它们分割开)。
????????快速排序比到目前为止你学过的其他排序算法要复杂一些。让我们一步步地来学习。
(1) 首先,从数组中选择中间一项作为主元。
(2) 创建两个指针,左边一个指向数组第一个项,右边一个指向数组最后一个项。移动左指针直到我们找到一个比主元大的元素,接着,移动右指针直到找到一个比主元小的元素,然后交换它们,重复这个过程,直到左指针超过了右指针。这个过程将使得比主元小的值都排在主元之前,而比主元大的值都排在主元之后。这一步叫作划分操作。
(3) 接着,算法对划分后的小数组(较主元小的值组成的子数组,以及较主元大的值组成的子数组)重复之前的两个步骤,直至数组已完全排序。
让我们开始快速排序的实现吧:
var quickSort = function(array){
quick(array,0,array.length-1)
return array
}
var quick = function(array,left,right){
var index //{1}
if(array.length>1){ //{2}
index = partition(array,left,right) //{3}
if(left<index-1){ //{4}
quick(array,left,index-1) //{5}
}
if(index<right){
quick(array,index,right) //{7}
}
}
}
var partition = function(array,left,right){
var pivot = array[Math.floor((right+left)/2)], //{8}
i=left, //{9}
j=right //{10}
while(i<=j){ //{11}
while(array[i]<pivot){ //{12}
i++
}
while(array[j]>pivot){ //{13}
j--
}
if(i<=j){ //{14}
[array[i],array[j]]=[array[j],array[i]] //{15}
i++
j--
}
}
return i //{16}
}????????首先声明index(行{1}),该变量能帮助我们将子数组分离为较小值数组和较大值数组,这样,我们就能再次递归的调用quick函数了。partition函数返回值将赋值给index(行{3})。
????????如果数组的长度比1大(因为只有一个元素的数组必然是已排序了的(行{2}),我们将对给
定子数组执行partition操作(第一次调用是针对整个数组)以得到index(行{3})。如果子数组存在较小值的元素(行{4}),则对该数组重复这个过程(行{5})。同理,对存在较大值得子数组也是如此,如果存在子数组存在较大值,我们也将重复快速排序过程(行{7})。
1. 划分过程
????????第一件要做的事情是选择主元(pivot),有好几种方式。最简单的一种是选择数组的第一
项(最左项)。然而,研究表明对于几乎已排序的数组,这不是一个好的选择,它将导致该算法
的最差表现。另外一种方式是随机选择一个数组项或是选择中间项。
????????在本实现中,我们选择中间项作为主元(行{8})。我们初始化两个指针:left(低——行
{9}),初始化为数组第一个元素;right(高——行{10}),初始化为数组最后一个元素。
????????只要left和right指针没有相互交错(行{11}),就执行划分操作。首先,移动left指针直到找到一个元素比主元大(行{12})。对right指针,我们做同样的事情,移动right指针直到我们找到一个元素比主元小。
????????当左指针指向的元素比主元大且右指针指向的元素比主元小,并且此时左指针索引没有右指
针索引大(行{14}),意思是左项比右项大(值比较)。我们交换它们,然后移动两个指针,并
重复此过程(从行{11}再次开始)。
????????在划分操作结束后,返回左指针的索引,用来在行{3}处创建子数组。
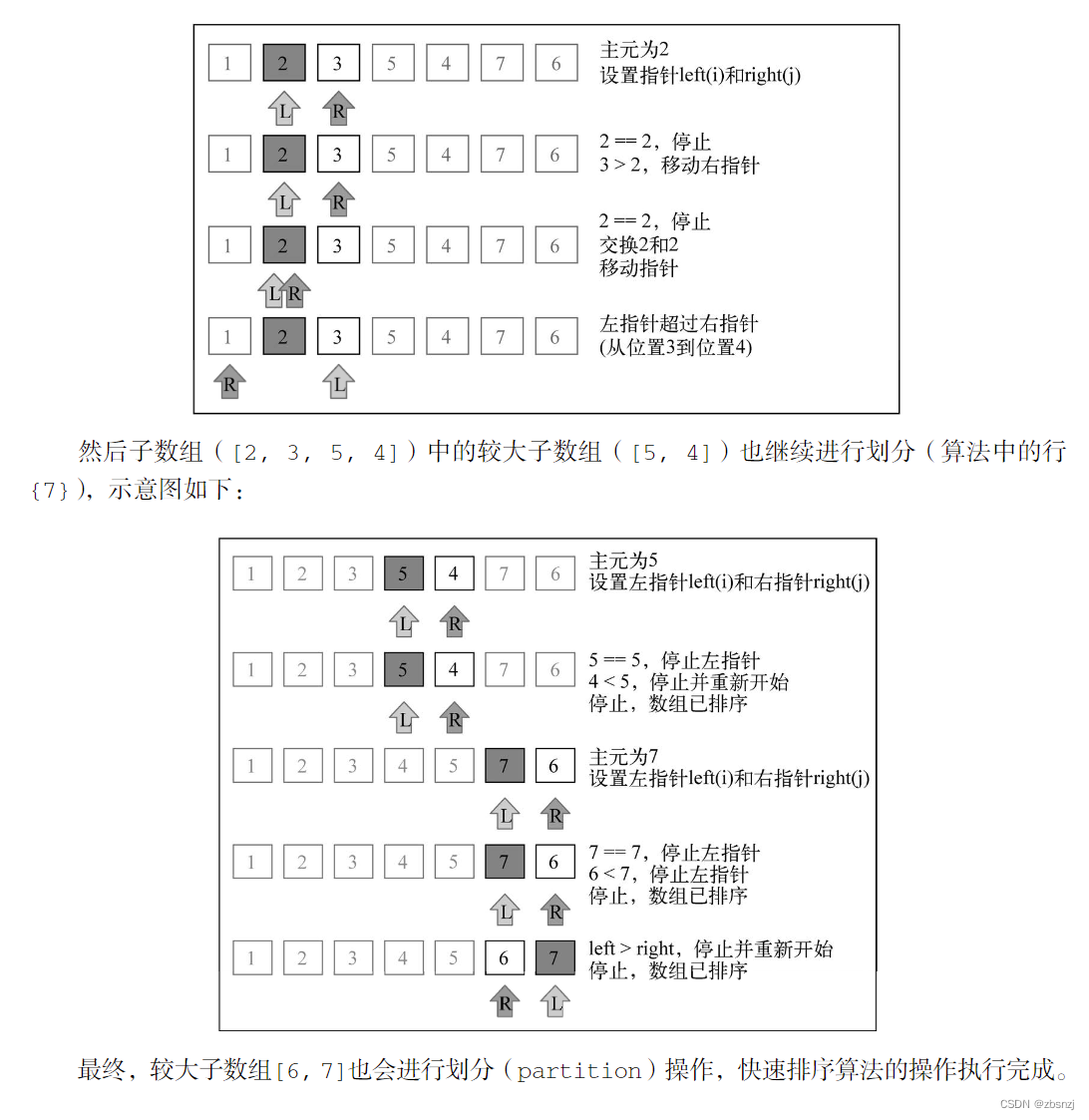
2. 快速排序实战
让我来一步步地看一个快速排序的实际例子:

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【MATLAB】ICEEMDAN+FFT+HHT组合算法
- Sortable.js:功能强大的JavaScript 拖拽库
- 【RocketMQ-Bug】RocketMQ 在使用中的常见问题
- Vmware Windows10安装Apache php
- 被忽视的暗面:客户端应用漏洞挖掘之旅
- 【Docker安装Redis】Docker安装Redis,读取Redis配置文件,支持远程访问
- 图文教程:从0开始安装stable-diffusion
- 子母导弹反无人机集群制导策略
- Java诊断利器Arthas
- HarmonyOS应用程序包快速修复命令调试开发指导