代码随想Day60 | 84.柱状图中最大的矩形
发布时间:2024年01月08日
84.柱状图中最大的矩形
这道题和接雨水遥相呼应,接雨水是求外部凹槽,这道题是求内部面积,这道题的整体思路是某一个元素,找到其左边的第一个小于该数的位置,右边的第一个小于该数的位置,然后以当前索引的高度为高度,宽度是左右两个位置中间的距离,这样就可以求出以这个位置为基准的最大面积。但是这道题有一个着重强调的细节:
(下述原文来自代码随想录)
height数组前后都加一个元素0。
首先来说末尾为什么要加元素0?
如果数组本身就是升序的,例如[2,4,6,8],那么入栈之后 都是单调递减,一直都没有走 情况三 计算结果的哪一步,所以最后输出的就是0了。 如图:
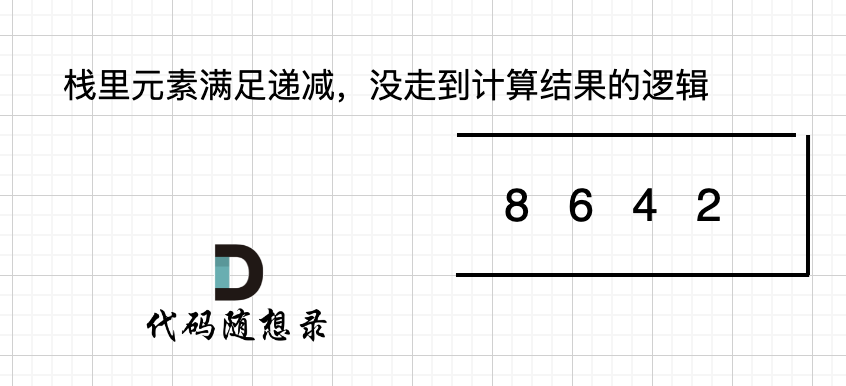
那么结尾加一个0,就会让栈里的所有元素进入被弹出的逻辑。
开头为什么要加元素0?
如果数组本身是降序的,例如 [8,6,4,2],在 8 入栈后,6 开始与8 进行比较,此时我们得到 mid(8),rigt(6),但是得不到 left。
(mid、left,right 都是对应版本一里的逻辑)
因为 将 8 弹出之后,栈里没有元素了,那么为了避免空栈取值,直接跳过了计算结果的逻辑。
之后又将6 加入栈(此时8已经弹出了),然后 就是 4 与 栈口元素 8 进行比较,周而复始,那么计算的最后结果resutl就是0。 如图所示:
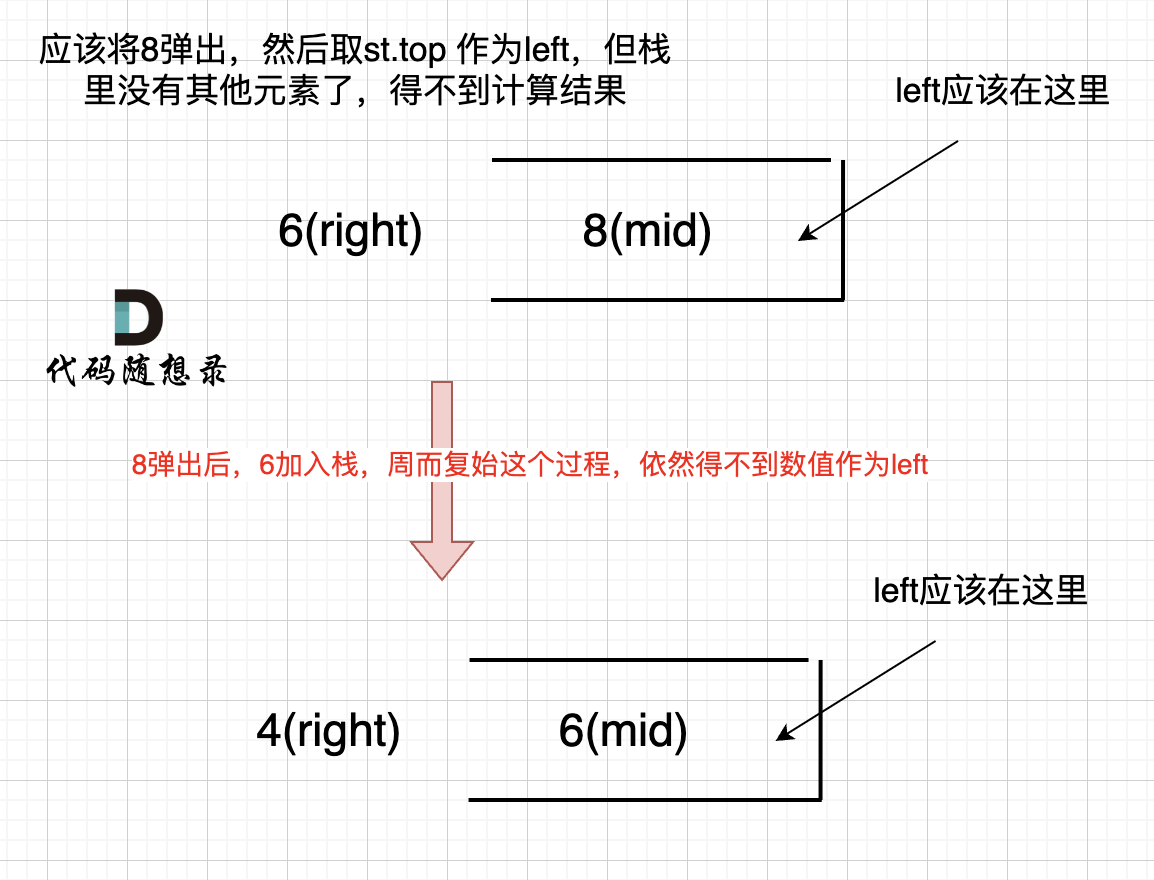
所以我们需要在 height数组前后各加一个元素0。
详细代码如下:
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> s;
heights.insert(heights.begin(),0); //首尾加0.trick
heights.push_back(0);
s.push(0);
int res = 0;
for(int i=1;i<heights.size();i++)
{
while(!s.empty()&&heights[i]<heights[s.top()])
{
int h = heights[s.top()];
s.pop();
if(!s.empty())
{
int w = i-s.top()-1;
res = max(res,h*w);
}
}
s.push(i);
}
return res;
}
};
文章来源:https://blog.csdn.net/juantingliu_01/article/details/135463978
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- JavaScript中如何将数字金额转换为大写人民币汉字
- 湖南大学-算法设计与分析-2023期末考试【原题】
- 西瓜书读书笔记整理(十二) —— 第十二章 计算学习理论
- 【samba】自动共享所有用户家目录
- 中国社科院-新加坡新跃社科大学工商管理博士(DBA)项目课程设置
- GPT4+Python近红外光谱数据分析及机器学习与深度学习建模
- 使用自动化测试获取手机短信验证码
- 零成本搭建一款博客网站(基于Vercel+Hexo完美实现)【保姆级教程】
- new mars3d.control.LocationBar({实时获取到地球渲染后的帧率fps等信息
- 聊聊如今的前端