编译原理----算符优先级的分析（自底向上）

自底向上分析的分类如下所示：

算符优先分析

算符优先分析只规定算符之间的优先关系，也就是只考虑终结符之间的优先关系。

（一）若有文法G，如果G没有形如A->..BC..的产生式，其中B和C为非终结符，则称G为算符文法。

以下例子中G就是算符文法(没有连在一起的非终结符)

E->T|E+T|E-T

T->F|T*F|T/F

F->(E)|i

（二）

这里就用=，< 和 > 代替：?

（1）a=b,当且仅当G中含有形如A--->..ab...或A---->...aBb...的产生式

（2）a<b,当且仅当G种含有形如A--->...aB...的产生式，且B能多步推导出右侧式子

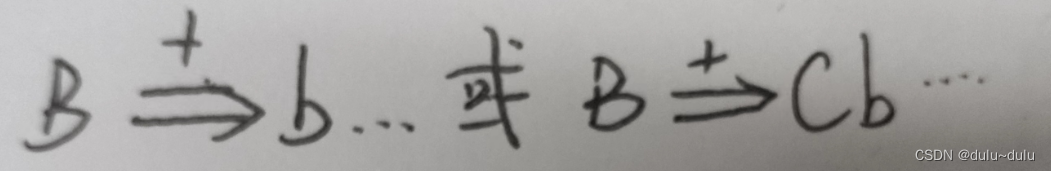
?（3）a>b,当且仅当G中含有形如A--->...Bb...的产生式，且B能多步推导出右侧式子

这里理解起来也很简单，a<b，那么a就要小于B推导出的式子中最前面的终结符b，a>b同理

这里的推导较为复杂，我们可以演化出下面这一方法：

这样a<b，a>b的定义就为：

a<b,当且仅当G种含有形如A--->...aB...的产生式,且a小于B的FIRSTVT集合中的所有终结符

a>b,当且仅当G中含有形如A--->...Bb...的产生式,且B的LASTVT的所有终结符大于b

构造规则：

FIRSTVT:

(1)若有T->a...或T->Ra...，则aFIRSTVT(T)

(2)若有aFIRSTVT(R),且有产生式T->R...，则aFIRSTVT(T)

LASTVT：

(1)若有T->...a或T->...aR,则aLASTVT(T)

(2)若aLASTVT(R),且产生式T->...R，则aLASTVT

（三）设有一个不含产生式的算符文法G，如果任一终结符对（a,b）之间至多只有<,>,=3种关系种的一种成立，则称G是一个算符优先文法。即，两个终结符之间的优先关系是有序的，允许有a>b,b<a同时存在，但是不允许有a<b,a>b,a=b3种关系中的任一两种关系同时存在。

示例：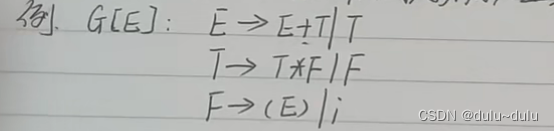

FIRSTVT集合：

(1)首先根据E->E+T|T的E->E+T，可得(注：行代表终结符，列代表非终结符)

(2)再看E->E+T|T?的E->T，需要把T的FIRSTVT元素放到E中，但是此时T中没有?元素，所以

?(3)T->T*F|F中的T->T*F

(4)T->T*F|F中的T->F，而F没有?项

?(5)F->(E)|i 中的F->(E)

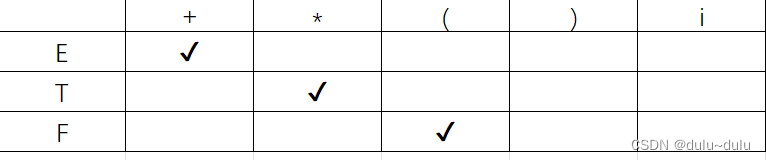
(6)F->(E)|i 中的F->i

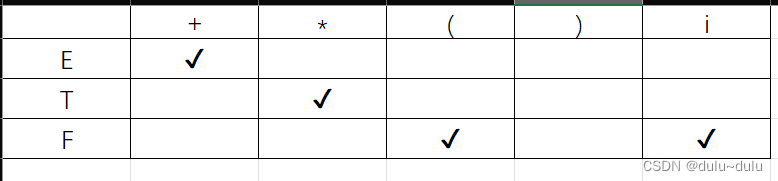
这是第一遍遍历式子，因为表有变化，所以要继续进行遍历，直到表不变

(1)首先根据E->E+T|T的E->E+T，可得

(2)再看E->E+T|T?的E->T，需要把T的FIRSTVT元素放到E中

(3)T->T*F|F中的T->T*F

(4)T->T*F|F中的T->F，将F中的?项放到T中

表依旧有改变，继续遍历，直到没有出现新的内容

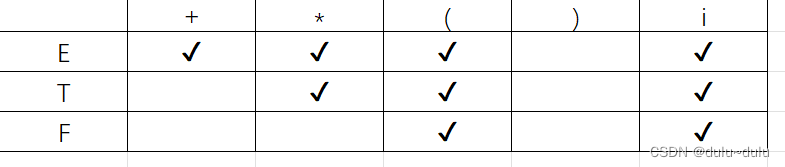
所以得出结论：
E（FIRSTVT）={+，*，{，}，i}

T（FIRSTVT）={*，（，i}

F（FIRSTVT）={（，i}

LASTVT的操作步骤同理，得到：

接下来继续回到算符优先关系中

竖列表示在前面的终结符，横列表示在后面的终结符

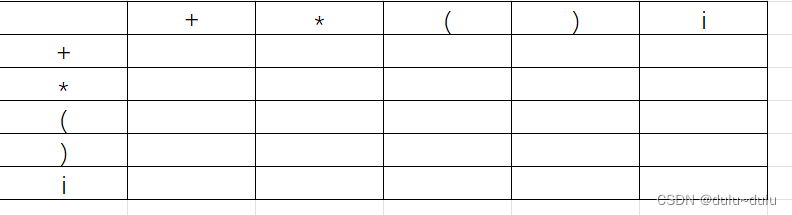
针对a=b

?F->(E)|i,这里的“（”和“）”遵循a=b的定义，即A->..aBb...

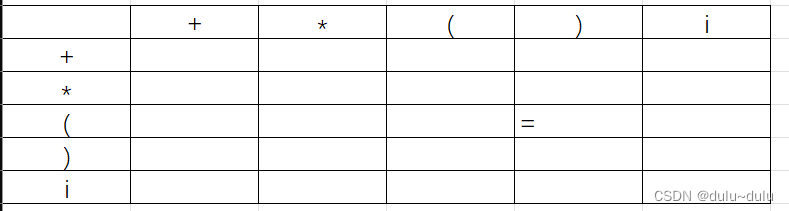
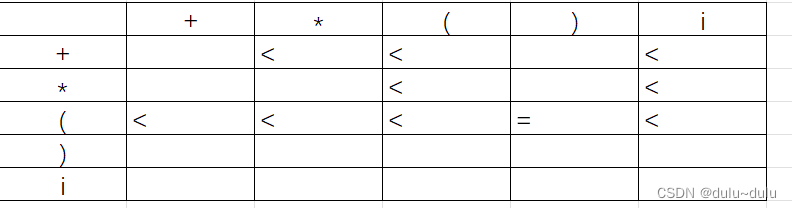
针对a<b,就是要找到a后面跟的非终结符,这个非终结符中的FIRSTVT集合的元素就是满足要求的元素。

E->E+T|T中的+T，T（FIRSTVT）=?{*，（，i}

T->T*F|F中的*F，F（FIRSYVT) =?{（，i}

F->(E)|i中的(E，E（FIRSTVT）=?{+，*，{，}，i}

针对a>b,就是要找到a前面跟的非终结符，这个非终结符中的LASTVT集合的元素就是满足要求的元素：

E->E+T|T中的E+

T->T*F|F的T*

F->(E)|i 的E）

最终得到：

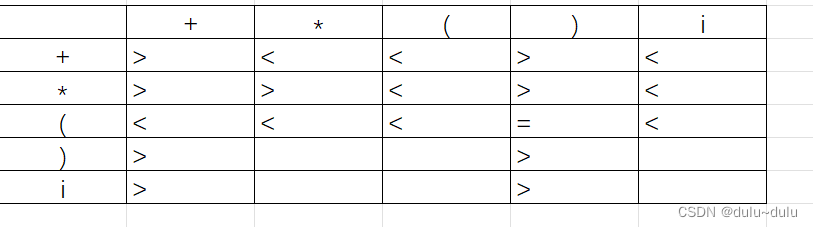
总结：

对于a<b,就要找终结符后面的非终结符（*F）的FIRSTVT集合（F的FIRSTVT集合）

对于a>b,就要找终结符前面的非终结符（F*）的LASTVT集合（F的LASTVT集合）