用加法器实现补码的加/减运算

目录

1.原码的加减运算

（1）原码的加/减法运算

（2）溢出判断

（3）符号扩展

2.加法器原理

3.加法器实现补码的加减运算

---

1.原码的加减运算

（1）原码的加/减法运算

正+正--->绝对值做加法，结果为正

负+负--->绝对值做加法，结果为负
正+负--->绝对值大的减绝对值小的，符号同绝对值大的数

负+正--->绝对值大的减绝对值小的，符号同绝对值大的数

原码的减法运算，只需要将“减数”符号取反，就可以转变为加法运算

对于正+正，负+负的情况，结果可能会溢出，例如：

A=15，B=-24，C=124：

[A+C]补=0,0001111+0,1111100=1,0001011 真值-117，A+C=15+124，不是-117，这就发生了溢出，8位补码的范围是-128~127

[B-C]补=1,1101000+1,0000100=0,1101100 真值+108，同样溢出，-24-124（两个负数相加得到正数）

?对于补码加减不会的可以看看：http://t.csdnimg.cn/4oTZI

（2）溢出判断

只有“正数+正数”才会上溢---正+正=负

只有“负数+负数”才会下溢---负+负=正

例如：2+2，可以理解为2向右再移动两格，那么就到了-4

计算机判断溢出有3种方式：

1.采用一位符号位，设A的符号为（被加数正负号），B的号为（加数的正负号），运算结果的符号为（运算结果的正负号），则溢出逻辑表达式为

若V=0，表示无溢出；

若V=1，表示有溢出。

也就是：

:如果正（1）+正（1）=负（0）

:如果负（0）+负（0）=正（1）

都表示溢出

例如

[A+C]补=0,0001111+0,1111100=1,0001011

被加数符号为0，加数符号为1，运算结果的符号1，得到V=1，表示有溢出

?

2.采用一位符号位，根据数据位进位情况判断溢出符号位的进位Cs，最高数值位的进位C1

若符号位进位Cs=0，C1=1,表示发生上溢

若符号位进位Cs=1，C1=0,表示发生下溢

即Cs与C1不同时有溢出，所以可以用异或表示：Cs??C1=1表示不同，=0表示相同

Cs与C1的含义如下图所示：?

3.采用双符号位，正数符号为00，负数符号为11

[A+C]补=00，0001111+00，1111100 =01,0001011? ? ? ? 上溢

[B-C]补=11，1101000+11，0000100 =10,1101100? ? ? ?下溢

记两个符号位为S1S2，则V=S1S2，若V=0，表示无溢出;若V=1，表示有溢出。

第一个符号位表示正确的正负性，第二个符号位表示实际的符号结果

例如，01，0表示正确符号位应该为正，实际却得到了1（负数），发生上溢

实际存储时，只会存储1个符号位，再运算前会复制一个符号位，运算时两个符号位会同时参与运算。 所以采用双符号位并不会增加存储空间。

注：双符号位补码又称：模4补码，单符号位补码又称：模2补码

01,0001011，如果我们将，看作 . 即01.0001011，那么0()1().0001011?

模4就是相当于将位权小于4的部分保留，将大于4的部分舍弃,模2同理

（3）符号扩展

对于正整数，由于原，反，补码都是一样的，所以

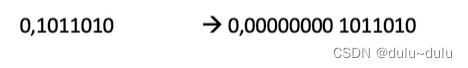
对于负整数：

反码：在原码的基础上数值位补1

补码：在原码中找到最右边的1，将其左边的数值位全部取反

对于正小数，原，反，补码的表示都一样

对于负小数：
反码：在原码的基础上后半部分补1

补码：在原码的基础上，找到最右边的1，左半部取反，右半部分不变

由于原码的加减运算用电路实现比较复杂，所以通常用补码进行加减运算

2.加法器原理

Cin表示来自低位的进位，Cout表示来自最高位的进位

A=1000，B=0111，Cin=0,那么算式就为

1 0 0 0

0 1 1 1

+? ? ? ?0

----------

1 1 1 1

所以F=1111，因为最高位没有进位，所以Cout=0

A=1000,B=0111，Cin=1，那么算式就为

? ?1 0 0 0

? ?0 1 1 1

? ?+? ? ? ?1
??----------

1 0 0 0 0

所以F=0000，Cout=1

若想实现8bit加法器，那么可以将两个加法器串联起来，高位的Cin能接收来自地位的Cout

3.加法器实现补码的加减运算

首先看一下补码加减运算的方法：

补码X+Y：按位相加即可

补码X-Y：将补码Y全部按位取反，末位+1，得到[-Y]补，即X+[-Y]补，减法/变加法

这里可以这样理解，Y的最高位取反得到-Y，再将除最高位的其他位取反+1，得到[-Y]补

也就是将补码Y全部按位取反，末位+1

例如：

4bit补码，X=-8，Y=7，X补=1000，Y补=0111

对于4bit有符号的补码，有效范围是~= -8~7

X+Y=1111B

X-Y=1000+(1000+1)=10001=1D,运算结果只保留低四位，最高位进位丢弃（发生溢出），此时的运算结果是错误的

4bit补码，X=3，Y=4。X补=0011， Y补=0100

X+Y=0111B=7D

X-Y=0011+(1011+1) = 1111B=-1D

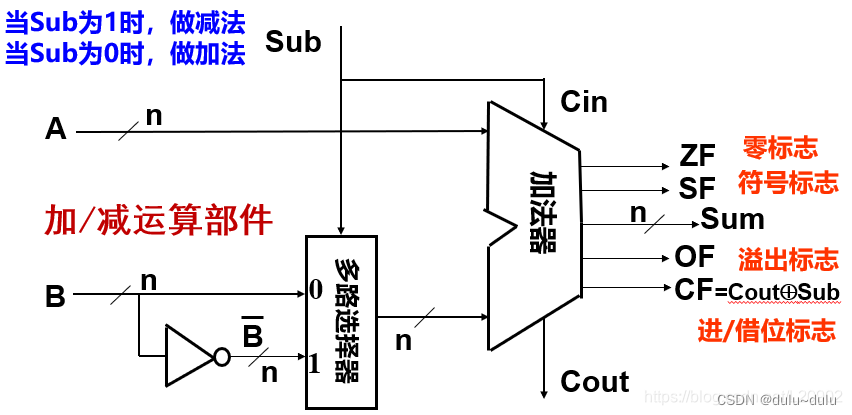
接下来看用加法器实现补码的加减运算：

Sub加/减控制信号：如果为加法则控制信号为0，如果为减法控制信号为1

当为加法时，控制信号为0，Cin=0，所以得到 X+Y+Cin=X+Y

当为减法时，控制信号为1，Cin=1，所以得到 X+Y+Ciin=X+（Y全部按位取反）+1

注:无符号整数的加/减法也可用该电路实现，且实现方法与有符号加减法一样，例如：

无符号数X=8，Y=7，用4bit表示，X=1000B，Y=0111B

X+Y=1111B=15D(十进制)

X-Y=1000+(1000+1)=10001=1D,运算结果只保留低4位，最高位进位丢弃，这个结果是正确的

对比一下有符号数：4bit补码，X=-8，Y=7，X补=1000， Y补=0111

X+Y=1111B=-1D

X-Y=1000+(1000+1)=10001=1D，这个运算结果是错误的

所以补码加减运算与无符号数加减运算都可以使用同一个电路使用，但是两者判断溢出的条件有所不同，这就需要标志位来区分

从下图可以看出，两个nbit的数相加，除了得到sum以外，还可以输出4个标志信息：OF,SF,ZF,CF

OF(Overflow Flag)溢出标志。溢出时为1,否则置0

注：OF只在有符号的加减运算中有意义，也就是说在无符号数的加/减运算中，即使OF=1，也不能说明发生了溢出

OF的计算方法：OF=最高位产生的进位次高位产生的进位

SF(Sign Flag) 符号标志。结果为负时置1,否则置0

计算方法：SF=最高位的本位和

SF同样只对有符号数有意义

ZF(Zero Flag)零标志，运算结果为0时ZF位置1,否则置0

ZF对有符号数，还是无符号数都是有意义的

CF(Carry Flag)进位/借位标志，进位/借位时置1,否则置0

CF=最高位产生的进位sub控制信号

只对无符号数有意义，对有符号数无意义

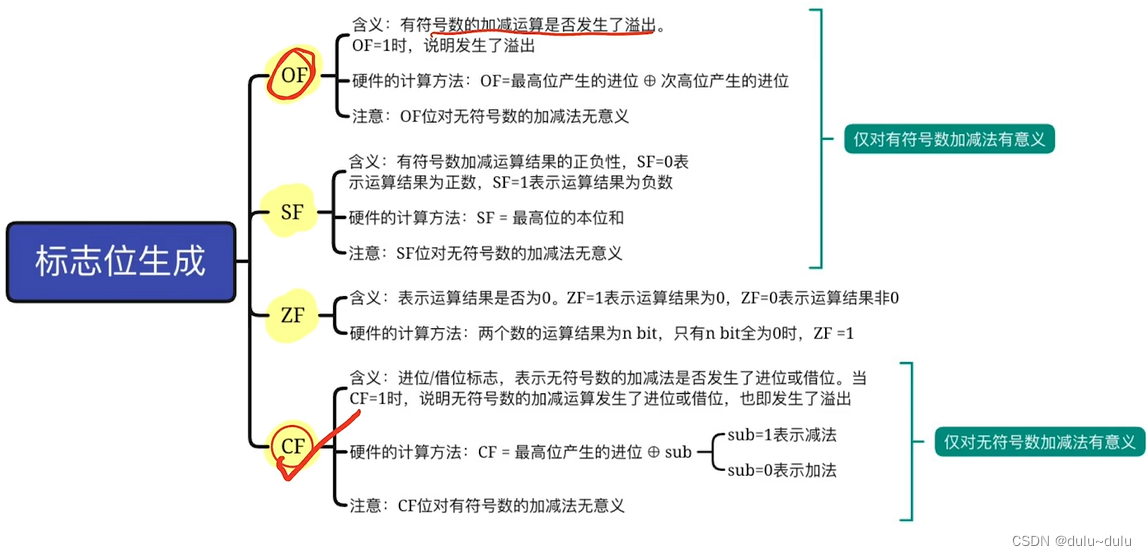
所以：对于有符号数的运算看OF，判断是否发生溢出，对于无符号数的运算看CF，判断是否发生溢出

再来看

无符号数 X=3，Y=4，用4bit表示，X=0011B，Y=0100B

X+Y=0111B=7D

X-Y=0011+(1011+1)=1111B=15D，显然3-4=15是错误的，无符号数无法表示负数-1

?对比有符号数，运算结果是正确的：

4bit补码，X=3，Y=4。X补=0011B， Y补=0100B

X+Y=0111B=7D

X-Y=0011+(1011+1) = 1111B=-1D

所以我们可以看到，虽然同一电路得到的二进制结果相同，但是有符号数的运算结果与无符号数的运算结果是有所不同的。