原码、反码、补码

原码、反码、补码

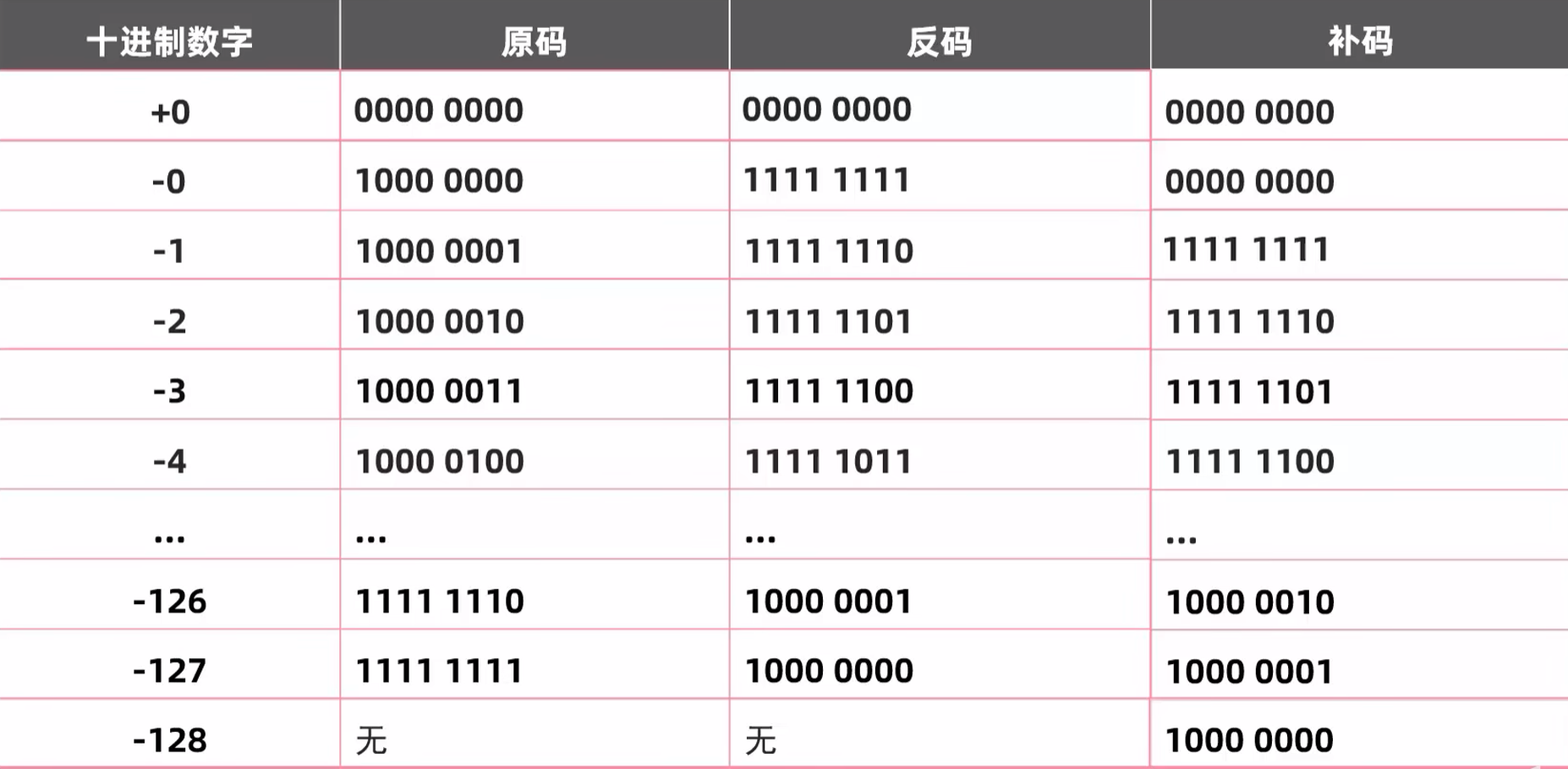
**原码：**十进制数据的二进制表现形式，最左边是符号位，0为正，1为负。

8个**bit**为一组（一个字节），是计算机中最小的计算单元。

利用原码对正数进行计算是不会有问题的。

原码的弊端

如果是负数计算，结果就出错，实际运算的结果，和我们预期的结果是相反的。

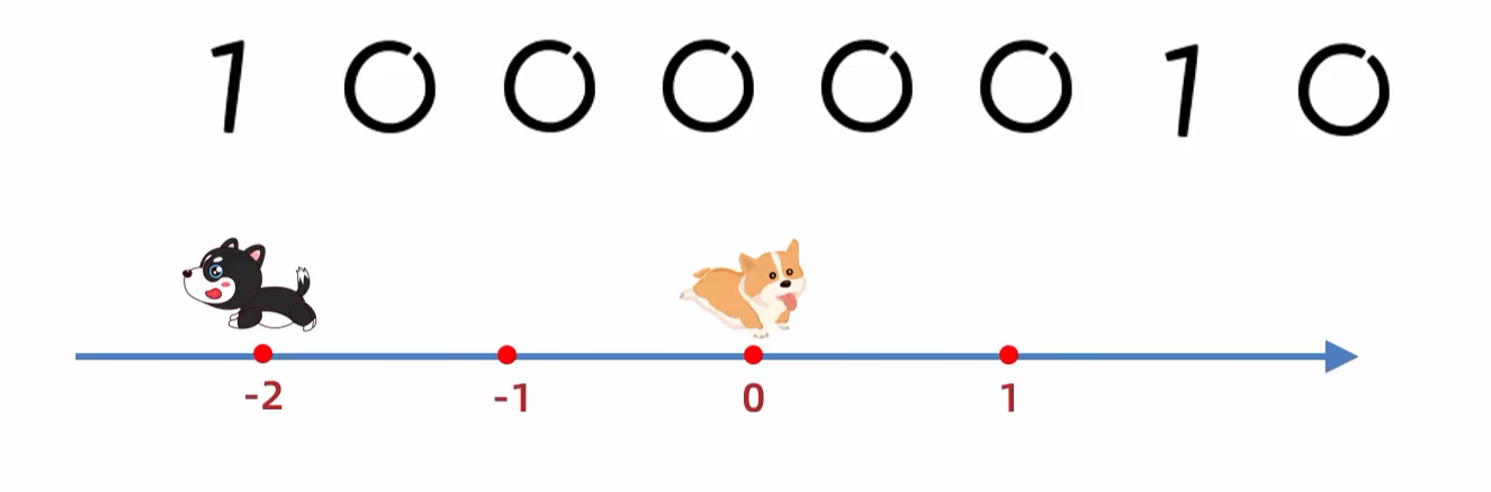
于是就出现了反码。

**反码：**为了解决原码不能计算负数的问题而出现的。

**计算规则：**正数的反码不变，负数的反码在原码的基础上，符号位不变。数值取反，0变1，1变0.

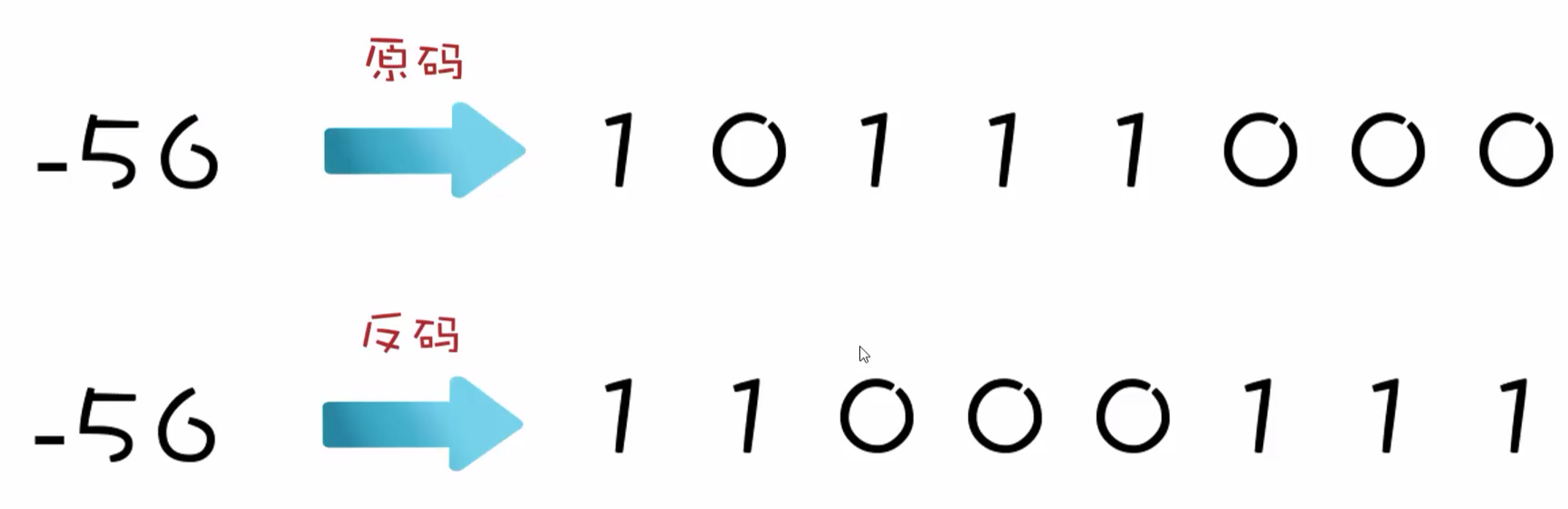
计算

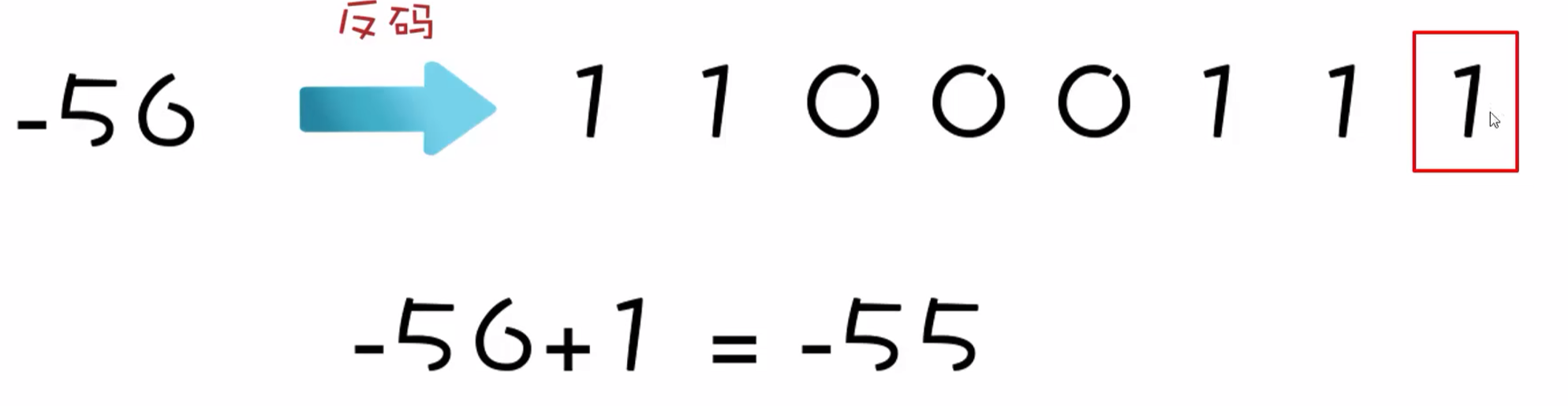
55的原码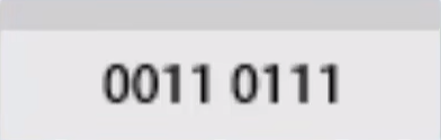

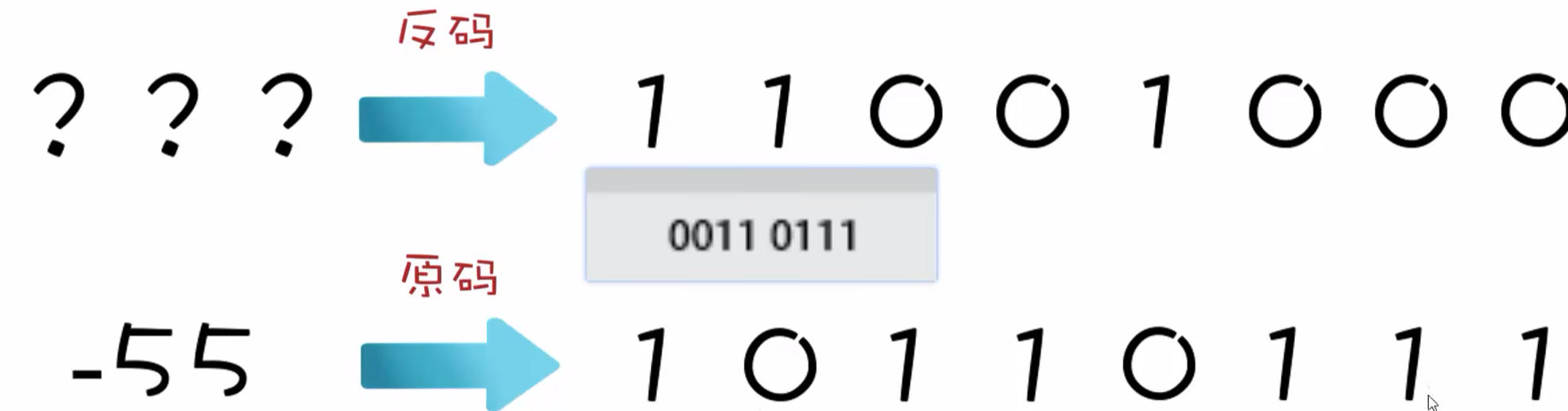
本该是3 结果却是2

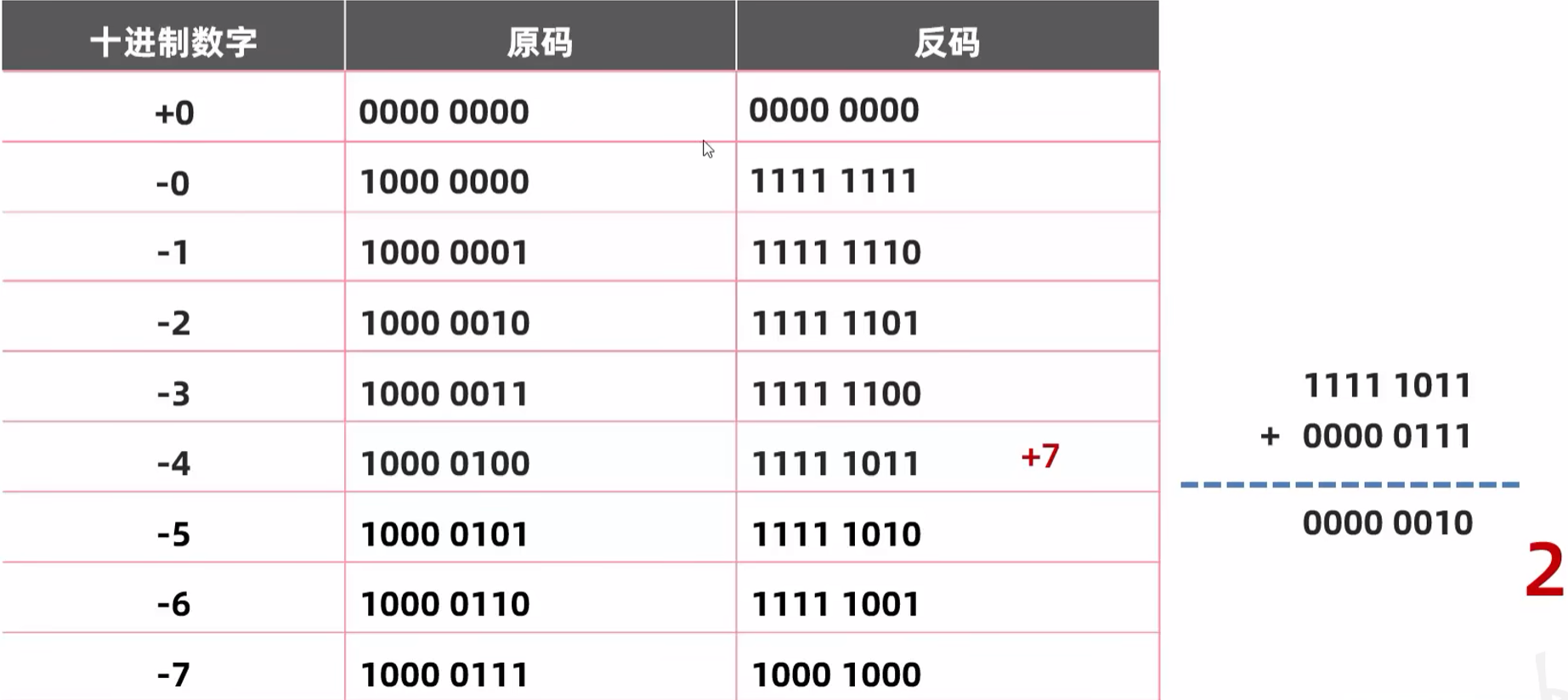
反码的弊端

反码中的0有两种表现形式。计算跨 0 会有一个1的误差。

于是，大佬们就想到了补码。

补码就是在反码的基础上**+1**.

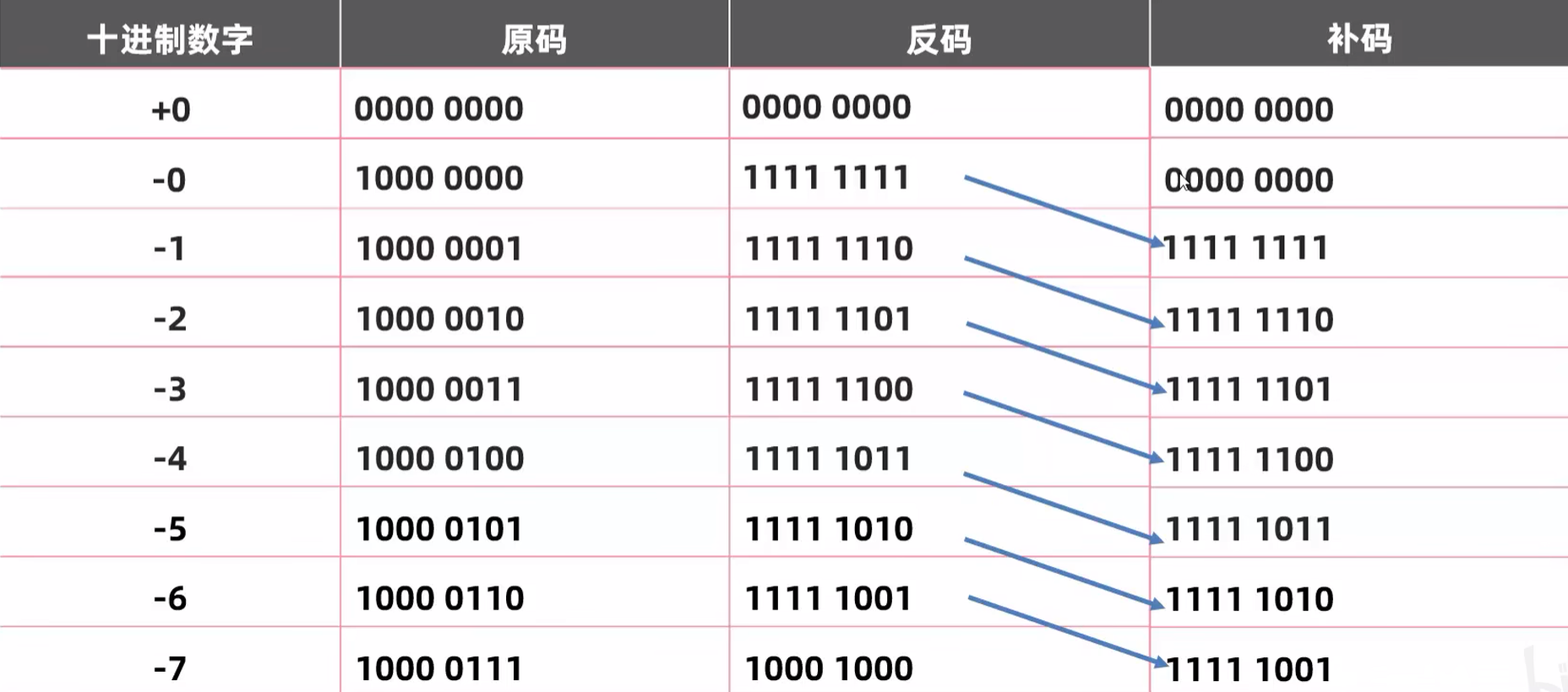
这样，就能把0的两种表现形式错掉了。

此时，正数的原码、反码、补码都还是一样的。

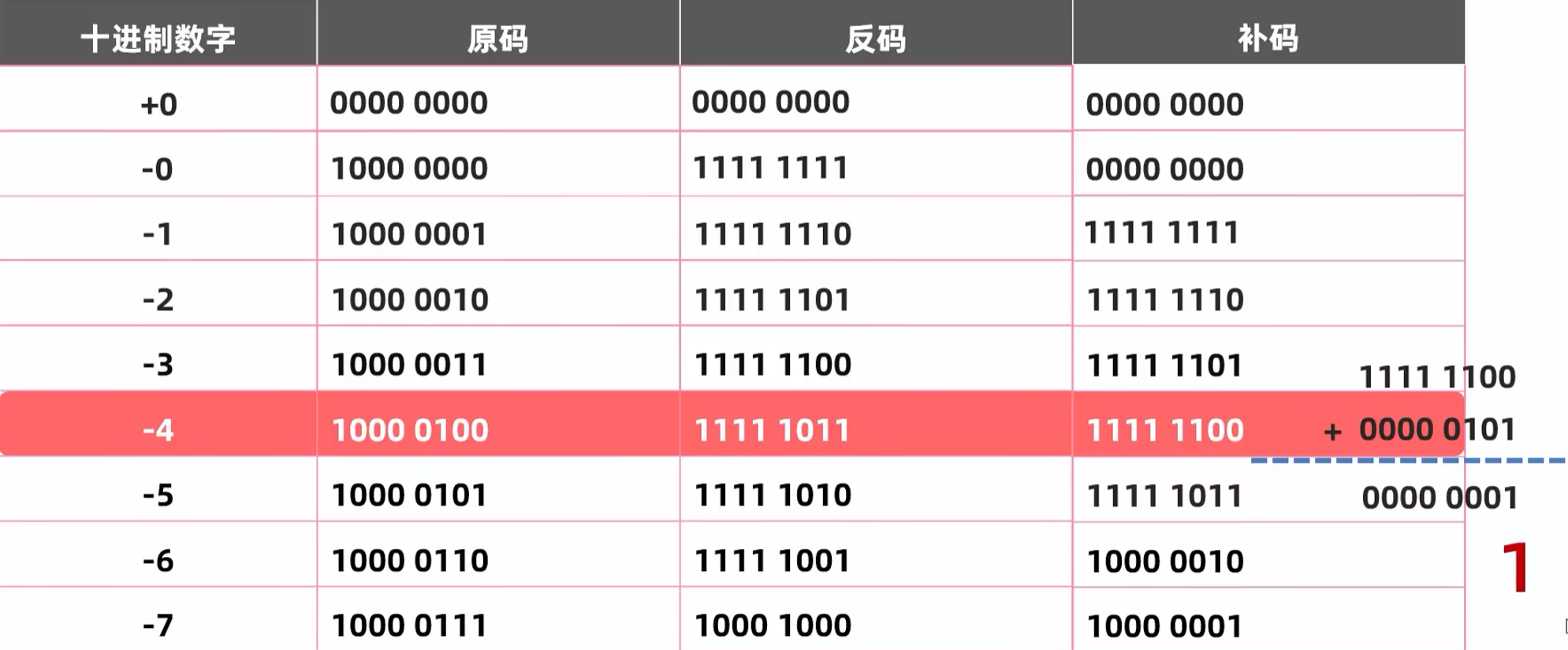
完美，这样补码就解决了计算机中正数和负数的计算问题。

补码的计算规则

正数的补码不变，负数的补码在反码的基础上+1。

另外补码还能多记录一个特殊的值-128，该数据在1个字节下，没有原码和反码。

计算机中的存储和计算都是以补码的形式进行的。

了解到了以上知识点，很多东西都能解释通了。

隐式转换

public class Test {
	public static void main(String[] args) {
    	byte a = 10;// 0000 1010
    	int b = a;  // 0000 0000 0000 0000 0000 0000 0000 1010
    	System.out.println(b);
    }
}

强制转换

public class Test {
	public static void main(String[] args) {
    	int a = 300;// 0000 0000 0000 0000 0000 0001 0010 1100
    	byte b = (byte)a;// 0010 1100
    	System.out.println(b);//44
    }
}

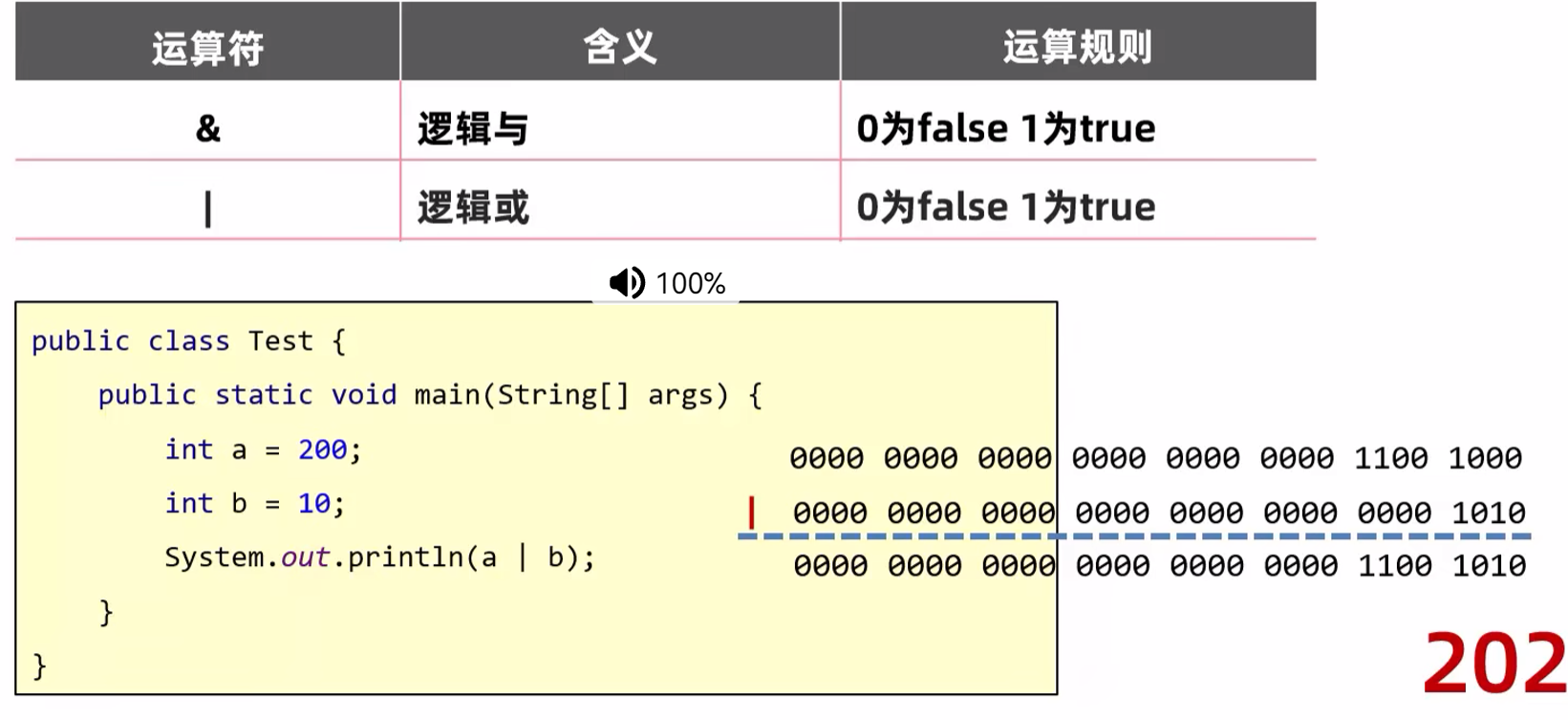
public class Test {
	public static void main(String[] args) {
    	int a = 200;// 0000 0000 0000 0000 0000 0000 1100 1000
    	byte b = (byte)a;// 1100 1000
    	System.out.println(b);// -56
    }
}

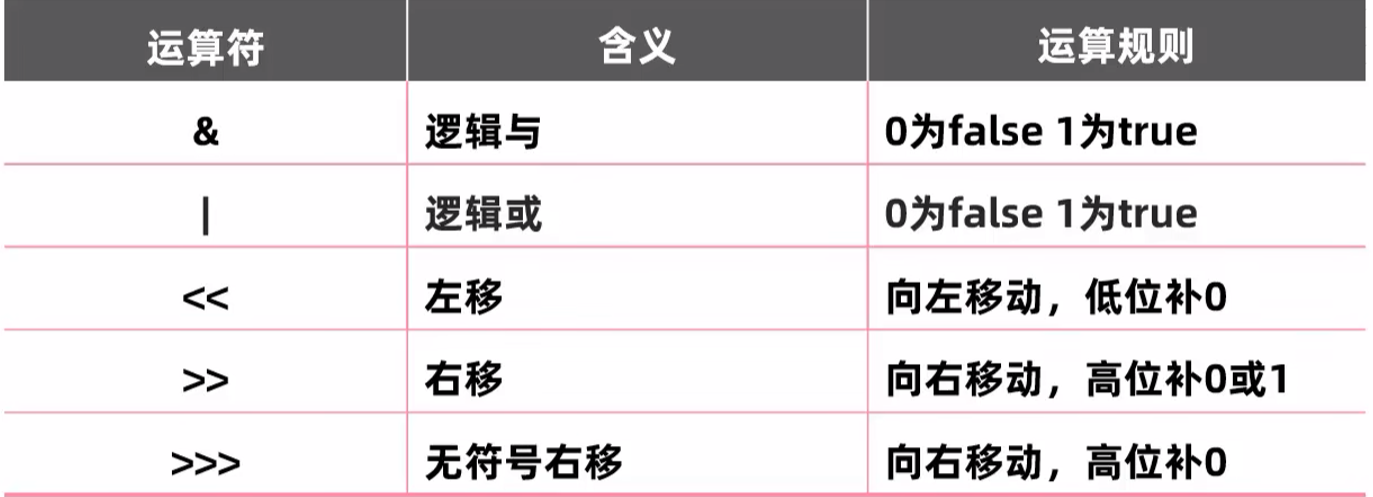
其他的运算符

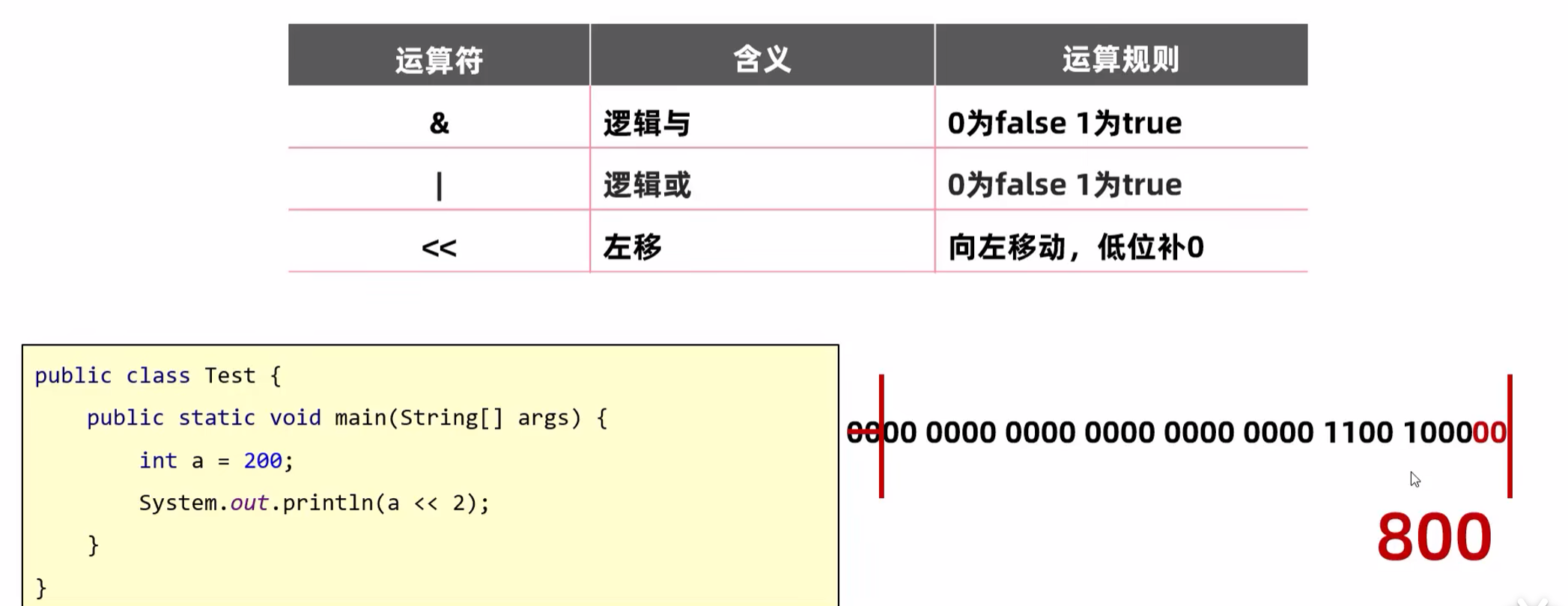
左移一次就乘2.

右移一次就除以2.