C++数据结构队列
队列
队列也是一种特殊的线性表,是限制在表的一端进行插入和在另一端进行删除的线性表。表中允许插入的一端称为队尾(rear),允许删除的一端称为队头(front)。当表中没有元素时称为空队列。队列的插入运算称为进队列或入队列,队列的删除运算称为退队列或出队列。
如图所示为队列的入队列和出队列的过程示意图,入队列的顺序是e1、e2、e3、e4、e5,出队列的顺序为e1、e2、e3、e4、e5,所以队列又称为先进先出线性表(First In First Out),简称FIFO表。其特点是先进先出或者后进后出。

顺序队列
与线性表一样,队列的实现也有顺序存储和链式存储两种方法。
顺序存放的队称为顺序队,要分配一段连续的内存空间存放元素。因为队列的头和尾都是活动的,所以需要一个队头指针和队尾指针。初始时,队头和队尾指向-1,入队操作之后队头指向第一个元素,队尾指向最后一个元素。
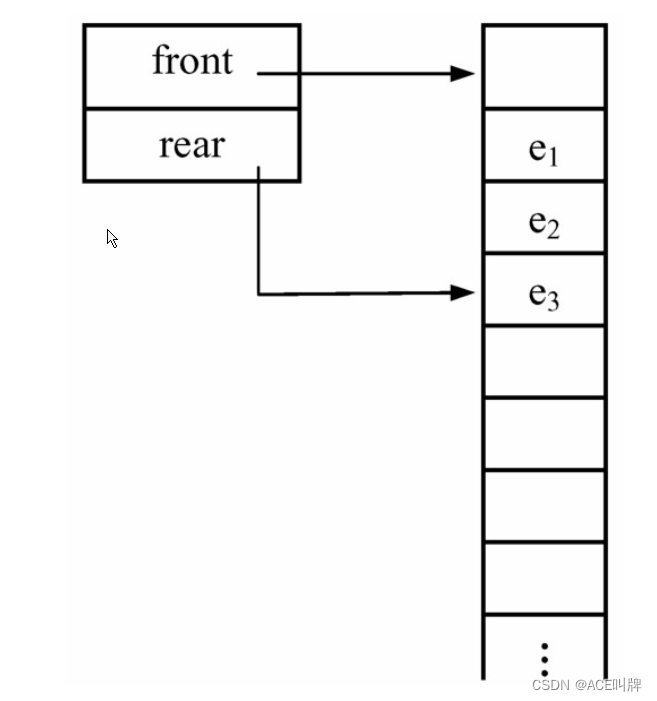
由于顺序队列是静态分配存储,队列的操作是一个动态过程:入队操作是在队尾rear加1的位置插入一个元素,rear移到空间的最后一个位置时队满;出队操作是在队头删除一个元素,有两种方法,第一种是将所有的队列元素向前移一位,rear减1, front始终指向0位置不变,就像排队时,队头总是固定在一个位置不变,每出队列一个人,其余的人向前走一个位置;另一种方法是不需要移动元素,修改队列头指针front加1,一般常采用第二种方法。
但第二种方法存在假溢出的情况。顺序存储结构存在溢出的情况,即表中元素的个数达到并超过实际分配的内存空间时溢出,这是正常的,队列也存在这种情况;但是队列还存在另外一种假溢出的情况,由于在出队删除元素时为了避免移动元素,只是修改了队头指针,这就会造成随着入队、出队的进行,队列整体向后移动,出现了图4.12所示的情况:队尾指针已经移到最后,再有元素入队就会出现溢出,而事实上,此时队中并未真的“满员”,这种现象为“假溢出”。
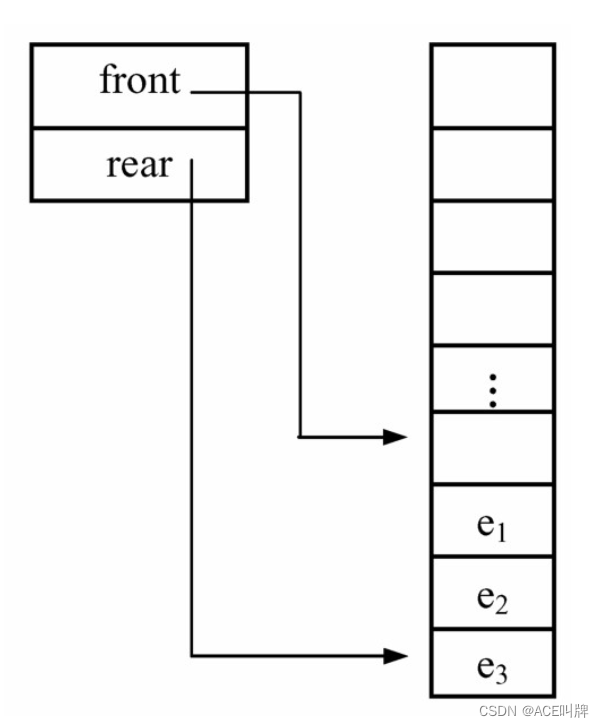
解决假溢出的方法之一是将队列的数据区看成头尾相接的循环结构,头尾指针的关系不变,将其称为“循环队列”。“循环队列”的示意图如图所示。
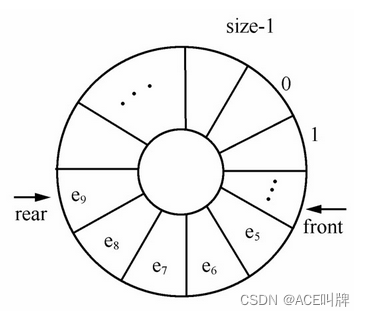
因为是头尾相接的循环结构,入队时的队尾指针加1操作修改为:rear=(rear+1)% size; (size为顺序队列空间的大小),出队时的队头指针加1操作修改为:front=(front+1)% size。
下面讨论队列空和满的条件。队空的条件:front=rear;队满的条件:如果队列的入队比出队快,队列中元素逐渐增多, rear会追上front,此时队满front=rear。因此,队空的条件和队满的条件相同,无法判断。这显然是必须要解决的一个问题。
方法之一是附设一个存储队中元素个数的变量,如num,当num=0时为队空,当num=size时为队满。
另一种方法是少用一个元素空间,使队尾指针rear永远赶不上front,即当队尾指针加1就会从后面赶上队头指针时,就视为队满。在这种情况下,队满的条件是:(rear+1)% size=front,就能和空队区别开。
顺序表的类描述
typedef int DataType; // 以整形为队列的数据类型
class SeqQueue
{
public:
SeqQueue();
~SeqQueue();
bool IsEmpty(); // 判断队列是否为空
bool Push(DataType e); // 入队
bool Pop(DataType& e); // 出队
bool GetTop(DataType& e); // 获取队头元素
private:
DataType* base_;
int front_; // 队头
int real_; // 队尾
int size_;
};
SeqQueue::SeqQueue(int _queueSize)
{
base_ = new DataType[_queueSize];
front_ = real_ = -1;
size_ = _queueSize;
}
SeqQueue::~SeqQueue()
{
delete[] base_;
}
(1)判断队列是否为空
bool SeqQueue::IsEmpty()
{
return (front_ == real_);
}
(2)入队操作
算法思想:首先判断队是否已满,若满则退出,否则,由于队的rear指向队尾元素,先修改rear到新的队尾位置,再将入队元素赋到rear的位置即可。
bool SeqQueue::Push(DataType e)
{
if ((real_ + 1) % size_ != front_)
{
if (front_ == -1)
front_ = 0;
real_ = (real_ + 1) % size_;
base_[real_] = e;
return true;
}
return false;
}
(3)出队操作
算法思想:首先判断队列是否为空,若空则退出,否则,由于队列的front指向队头元素的前一位置,因此要先修改front,再将其front所指向的元素以引用参数e返回即可。
bool SeqQueue::Pop(DataType& e)
{
if (!IsEmpty())
{
e = base_[front_];
// 说明只有一个元素
if (front_ == real_)
front_ = real_ = -1;
else
front_ = (front_ + 1) % size_;
return true;
}
return false;
}
(4)获取队头元素
算法思想:首先判断队是否为空,若空则退出,否则,由于队列的front指向队头元素的前一位置,因此要返回的队头元素是front的后一位置。
bool SeqQueue::GetTop(DataType& e)
{
if (!IsEmpty())
{
e = base_[front_];
return true;
}
return false;
}
链队列
队列的链式存储就是用一个线性链表来表示队列,称为链队。一般链栈用单链表表示。为了操作上的方便,需要一个头指针和尾指针分别指向链队列的队头和队尾元素,其结点结构与单链表的结构相同,即结点为:
typedef int DataType;
struct QueueNode
{
DataType data_;
QueueNode* next_;
QueueNode()
{
next_ = nullptr;
}
};
如图所示,front指向链队的队头元素,rear指向链队的队尾元素。删除出队时只要修改队头指针,插入入队时只要修改队尾指针。
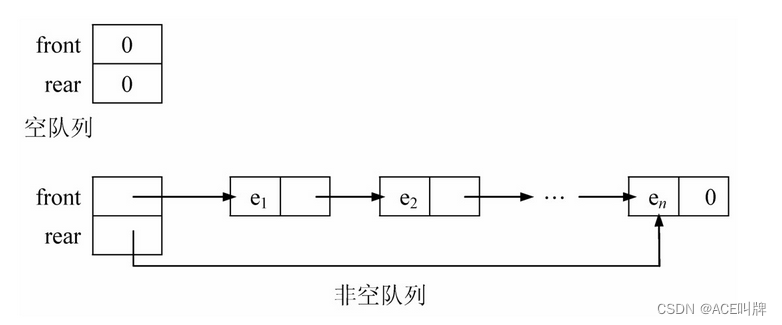
链式队的类描述
class LinkQueue
{
public:
LinkQueue();
~LinkQueue();
bool IsEmpty(); // 判断队列是否为空
bool Push(DataType e); // 入队
bool Pop(DataType& e); // 出队
bool GetTop(DataType& e); // 获取队头元素
private:
QueueNode* front_; // 队头指针
QueueNode* real_; // 队尾指针
int size_; // 元素个数
};
LinkQueue::LinkQueue()
{
front_ = nullptr;
real_ = nullptr;
size_ = 0;
}
LinkQueue::~LinkQueue()
{
QueueNode* p = front_, * q = nullptr;
while (p)
{
q = p;
p = p->next_;
delete q;
}
delete front_;
delete real_;
delete p;
}
(1)判断队列是否为空
算法思想:队头指针和队尾指针都为nullptr时队列为空
bool LinkQueue::IsEmpty()
{
return (front_ == nullptr && real_ == nullptr);
}
(2)入队操作
算法思想:首先申请结点,不成功则失败退出,否则,将申请的结点插入单链表的表尾。注意,此时如果原来的队列非空,只需修改队尾指针即可;若原来队列为空,则不仅要修改rear,还需要修改front后再返回成功标志。
bool LinkQueue::Push(DataType e)
{
QueueNode* p = new QueueNode;
if (p)
{
p->data_ = e;
if (real_)
{
real_->next_ = p;
real_ = p;
}
else
front_ = real_ = p;
size_++;
return true;
}
return false;
}
(3)出队操作
算法思想:首先判断队列是否为空,不为空则删除头结点,注意,此时如果原来的队列只有一个结点,则删除队头指针指向的结点后成了空队列,因此还要修改队尾指针。
bool LinkQueue::Pop(DataType& e)
{
if (!IsEmpty())
{
QueueNode* p = front_;
e = p->data_;
front_ = front_->next_;
// 如果队列中只有一个元素
if (!front_)
real_ = nullptr;
delete p;
p = nullptr;
return true;
}
return false;
}
(4)取队头元素
算法思想:首先判断队列是否为空,如果不为空取出头结点指向的值。
bool LinkQueue::GetTop(DataType& e)
{
if (!IsEmpty())
{
e = front_->data_;
return true;
}
return false;
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- midjourney教程【--niji 5】
- golang time.Newtimer和time.NewTicker使用和不同
- 【react.js + hooks】基于事件机制的跨组件数据共享
- BPF 程序与信号交互大揭秘
- 常见的Web攻击手段分析总结,实战案例:通过 X-Forwarded-Host 的密码重置令牌泄漏
- 一套系统搞定办公用品管理,行政工作省事不少!
- go 源码解读 - sync.Mutex
- 机器学习笔记--PageRank算法
- 商品信息管理系统:数字化高效处理企业进、销、存核心流程-亿发
- ant-design-vue Notification 通知提醒框 内容换行