【七】【C语言\动态规划】最大子数组和、环形子数组的最大和、乘积最大子数组,三道题目深度解析
动态规划
动态规划就像是解决问题的一种策略,它可以帮助我们更高效地找到问题的解决方案。这个策略的核心思想就是将问题分解为一系列的小问题,并将每个小问题的解保存起来。这样,当我们需要解决原始问题的时候,我们就可以直接利用已经计算好的小问题的解,而不需要重复计算。
动态规划与数学归纳法思想上十分相似。
数学归纳法:
-
基础步骤(base case):首先证明命题在最小的基础情况下成立。通常这是一个较简单的情况,可以直接验证命题是否成立。
-
归纳步骤(inductive step):假设命题在某个情况下成立,然后证明在下一个情况下也成立。这个证明可以通过推理推断出结论或使用一些已知的规律来得到。
通过反复迭代归纳步骤,我们可以推导出命题在所有情况下成立的结论。
动态规划:
-
状态表示:
-
状态转移方程:
-
初始化:
-
填表顺序:
-
返回值:
数学归纳法的基础步骤相当于动态规划中初始化步骤。
数学归纳法的归纳步骤相当于动态规划中推导状态转移方程。
动态规划的思想和数学归纳法思想类似。
在动态规划中,首先得到状态在最小的基础情况下的值,然后通过状态转移方程,得到下一个状态的值,反复迭代,最终得到我们期望的状态下的值。
接下来我们通过三道例题,深入理解动态规划思想,以及实现动态规划的具体步骤。
53. 最大子数组和

题目解析

动态表示
动态表示一般是通过经验+题目得到的。
经验一般是指,以某个位置为结尾,或者以某个位置为开始。
我们可以定义dp[i]表示以下标i为结尾的子数组,所能得到的最大和。
因为所有的子数组都有一个结尾,结尾的元素一定是nums数组的某一个元素。
所以我们可以用这个标准划分状态。
动态转移方程
我们想一想dp[i]的状态能不能由其他的状态推导得出?
dp[i]表示以下标i为结尾的子数组,所能得到的最大和。
dp[i-1]表示以下标i-1为结尾的子数组,所能得到的最大和。
对于以下标i为结尾的子数组,要么该子数组只有下标i一个元素,要么不止i下标一个元素。
如果只有下标i一个元素,那么dp[i]=nums[i]
如果不止下标i一个元素,那么dp[i]=dp[i-1]+nums[i]
因为dp[i]表示的是所能获得的最大和,所以在这两种情况中,我们需要选其中的更大的值。
故状态转移方程为,dp[i]=max(nums[i],dp[i-1]+nums[i])
初始化
根据状态转移方程,我们知道,想要推导出dp[i]需要用到dp[i-1]。
所以我们需要初始化第一个位置的状态,即初始化dp[0]。
dp[0]表示以下标0为结尾的子数组,所能得到的最大和。
很容易得到,dp[0]=nums[0]。
填表顺序
根据状态转移方程,我们知道,想要推导出dp[i]需要用到dp[i-1]。
所以我们应该从左往右填写dp表。
返回值
我们需要得到所有子数组中,最大的连续和,所以我们需要遍历所有情况,记录最大值。
代码实现
int maxSubArray(int* nums, int numsSize) {
//dp[i]表示以下标i结尾的连续子数组所能得到的最大和
int n=numsSize;
int dp[n];
int ret=nums[0];
dp[0]=nums[0];
for(int i=1;i<n;i++){
dp[i]=fmax(nums[i],dp[i-1]+nums[i]);
ret=fmax(dp[i],ret);
}
return ret;
}我们可以在填表的时候,每填写一个状态就比较一次,如果比最大值大就记录。
最后返回ret就是最大和。
918. 环形子数组的最大和

题目解析

动态表示
动态表示是由经验+题目意思得到的。
经验一般是以某个位置为结尾,或者以某个位置为开始。
根据题目分析,我们需要记录最大和和最小和。
所以我们应该定义f[i]、g[i],分别表示以i下标为结尾的子数组所能得到的最大和、最小和。
即,f[i]表示以i下标为结尾的子数组所能得到的最大和。
g[i]表示以i下标为结尾的子数组所能得到的最小和。
动态转移方程
我们想一想能不能由其他状态推导出f[i],g[i]?
f[i]表示以i下标为结尾的子数组所能得到的最大和。
g[i]表示以i下标为结尾的子数组所能得到的最小和。
f[i-1]表示以i-1下标为结尾的子数组所能得到的最大和。
g[i-1]表示以i-1下标为结尾的子数组所能得到的最小和。
对于f[i],以i下标为结尾的子数组,分两种情况,第一种情况是这个子数组只有i下标一个元素,第二种情况是不止i下标一个元素。
如果只有i下标一个元素,所能得到的最大和就是nums[i]本身。
如果不止i下标一个元素,所能得到的最大和就是f[i-1]+nums[i]。
所以f[i]=max(nums[i],f[i-1]+nums[i])
同理,g[i]=min(nums[i],g[i-1]+nums[i])
初始化
根据动态转移方程,我们知道想要推导出i下标状态需要用到i-1位置的状态。
所以我们需要初始化第一个位置的状态。
即,f[0]=nums[0],g[0]=nums[0]
填表顺序
根据状态转移方程,我们知道想要推导出i下标状态需要用到i-1位置的状态。
所以我们应该从左往右开始填写。
返回值

我们应该返回两种情况下的最大和。
要么最大和对应子数组在nums数组中间,要么最大和对应子数组在nums数组首尾。
当最大和对应子数组在nums数组中间时,我们只需要一个变量记录f[i]中的最大值即可
当最大和对应子数组在nums数组首尾时,我们需要一个变量记录g[i]中的最小值,然后还需要判断min是不是等于sum,如果是相等的,sum-min就没有意义。如果不相等,sum-min就是首尾情况的最大和。
返回这两种情况的最大和即可。
代码实现
int maxSubarraySumCircular(int* nums, int numsSize) {
int n=numsSize;
int sum=0;
for(int i=0;i<n;i++){
sum+=nums[i];
}
int f[n];
int g[n];
//f:最大和
//g:最小和
int max=nums[0],min=nums[0];
f[0]=nums[0];
g[0]=nums[0];
for(int i=1;i<n;i++){
f[i]=fmax(nums[i],f[i-1]+nums[i]);
g[i]=fmin(nums[i],g[i-1]+nums[i]);
max=fmax(max,f[i]);
min=fmin(min,g[i]);
}
return sum==min?max:fmax(sum-min,max);
}152. 乘积最大子数组
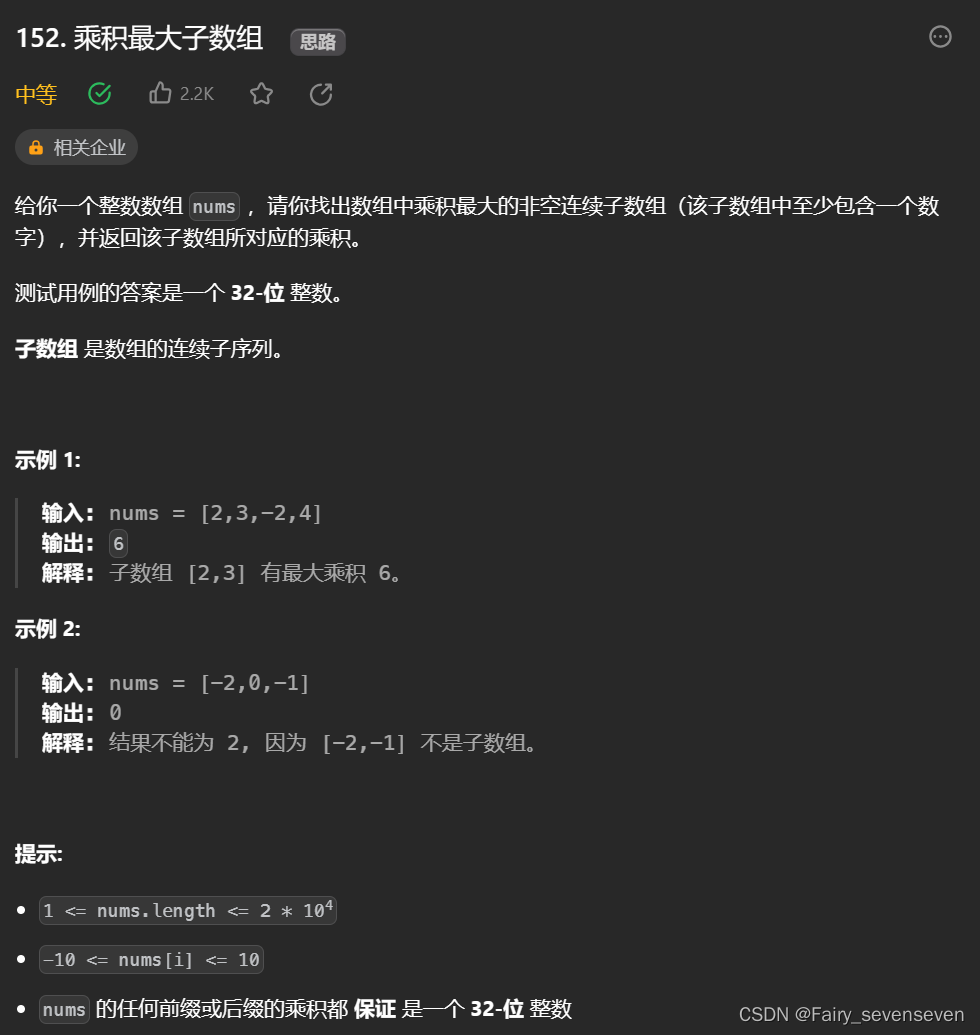
题目解析

动态表示
动态表示是由经验+题目意思得到的。
经验一般是以某个位置为结尾,或者以某个位置为开始。
根据题目意思我们需要求最大乘积值。
所以我们可以定义dp[i]表示以i下标结尾的子数组所能得到的最大乘积值。
(修正动态表示,f[i]表示以i下标结尾的子数组所能得到的最大乘积值
g[i]表示以i下标结尾的子数组所能得到的最小乘积值)
动态转移方程
我们想一想dp[i]能不能由其他状态推导得出?
dp[i]表示以i下标结尾的子数组所能得到的最大乘积值。
dp[i-1]表示以i-1下标结尾的子数组所能得到的最大乘积值。
(正数乘以最大值就是最大值,正数乘以最小值就是最小值)
(负数乘以最大值就是最小值,负数乘以最小值就是最大值)
对于dp[i],如果nums[i]>0,dp[i]=dp[i-1]*nums[i]
如果nums[i]<0,dp[i]=(i-1位置的最小乘积值)*nums[i]
所以我们发现只存储最大乘积值是不够的。所以我们修正动态表示。
(修正动态表示,f[i]表示以i下标结尾的子数组所能得到的最大乘积值
g[i]表示以i下标结尾的子数组所能得到的最小乘积值)
对于f[i],如果nums[i]>0,f[i]=f[i-1]*nums[i]
如果nums[i]<0,f[i]=g[i-1]*nums[i]
如果nums[i]=0,f[i]=0
对于g[i],如果nums[i]>0,g[i]=g[i-1]*nums[i]
如果nums[i]<0,g[i]=f[i-1]*nums[i]
如果nums[i]=0,f[i]=0
如果nums[i]=0,是可以把这种情况归类于nums[i]<0这种情况或者nums[i]>0这种情况中,因为当nums[i]=0,
f[i]=f[i-1]*nums[i]
f[i]=g[i-1]*nums[i]
g[i]=g[i-1]*nums[i]
g[i]=f[i-1]*nums[i]
都是等于0,所以动态转移方程可以写为
int x=nums[i]; int y=nums[i]*f[i-1]; int z=nums[i]*g[i-1]; f[i]=fmax(x,fmax(y,z)); g[i]=fmin(x,fmin(y,z));
初始化
根据动态转移方程,我们知道想要推导i位置的状态,需要i-1位置的状态,所以我们需要初始化第一个位置的状态。
即, f[0]=nums[0]; g[0]=nums[0];
填表顺序
根据状态转移方程,我们知道想要推导i位置的状态,需要i-1位置的状态,所以我们应该从左往右开始填写,同时填写两个表格。
返回值
f[i]表示以i下标结尾的子数组所能得到的最大乘积值
g[i]表示以i下标结尾的子数组所能得到的最小乘积值
我们要求的是最大乘积值,所以需要遍历f[i]数组中所有的值,找出最大值。
代码实现
int maxProduct(int* nums, int numsSize) {
int n=numsSize;
int f[n];
int g[n];
f[0]=nums[0];
g[0]=nums[0];
int ret=nums[0];
for(int i=1;i<n;i++){
int x=nums[i];
int y=nums[i]*f[i-1];
int z=nums[i]*g[i-1];
f[i]=fmax(x,fmax(y,z));
g[i]=fmin(x,fmin(y,z));
ret=fmax(ret,f[i]);
}
return ret;
}结尾
今天我们学习了动态规划的思想,动态规划思想和数学归纳法思想有一些类似,动态规划在模拟数学归纳法的过程,已知一个最简单的基础解,通过得到前项与后项的推导关系,由这个最简单的基础解,我们可以一步一步推导出我们希望得到的那个解,把我们得到的解依次存放在dp数组中,dp数组中对应的状态,就像是数列里面的每一项。最后感谢您阅读我的文章,对于动态规划系列,我会一直更新,如果您觉得内容有帮助,可以点赞加关注,以快速阅读最新文章。
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- kubelet源码分析(二):kubelet启动流程解析
- 利用 hexo 搭建 github page
- 基于微信支付的体育场馆预订小程序开发笔记一
- 跨国文件传输网络丢包的四大原因和修复方式
- 【第九节】变量与运算符-浮点类型的使用
- stylus、sass、less区别, Sass 、LESS是什么?大家为什么使用它们呢?postcss的作用
- 【Java基础】为什么重写equals()方法一定要重写hashCode()方法
- 【微服务】springcloud集成skywalking实现全链路追踪
- idea,pycharm激活成功,可以开始写代码了
- Linux 驱动开发基础知识——Hello驱动程序(一)