14、强化学习Soft Actor-Critic算法：推导、理解与实战

基于LunarLander登陆器的Soft Actor-Critic强化学习（含PYTHON工程）

Soft Actor-Critic算法是截至目前的T0级别的算法了，当前正在学习，在此记录一下下。

其他算法：
07、基于LunarLander登陆器的DQN强化学习案例（含PYTHON工程）

08、基于LunarLander登陆器的DDQN强化学习（含PYTHON工程）

09、基于LunarLander登陆器的Dueling DQN强化学习（含PYTHON工程）

10、基于LunarLander登陆器的Dueling DDQN强化学习（含PYTHON工程）

11、基于LunarLander登陆器的A2C强化学习（含PYTHON工程）
TRPO的LunarLander登陆器强化学习（含PYTHON工程）：
11.1、信赖域策略优化算法TRPO强化学习-从理论到实践
11.2、信赖域策略优化算法TRPO强化学习-约束优化求解
11.3、信赖域策略优化算法TRPO强化学习-运用实践
PPO的LunarLander登陆器强化学习（含PYTHON工程）：
13、近端策略优化Proximal Policy Optimization (PPO) 算法：从原理到实践
SAC的LunarLander登陆器强化学习（含PYTHON工程）：
14、强化学习Soft Actor-Critic算法：推导、理解与实战

参考：
Soft Actor Critic 详细推导与深入理解
SAC: Soft Actor-Critic Part 1

0、SAC算法简介

Soft Actor-Critic算法是截至目前的T0级别的算法，其综合了之前TRPO、PPO、TD3的优势：

1. TRPO and PPO: stochastic policies, on-policy, low sample efficiency，stable
2. DDPG and TD3: deterministic policies, replay buffer, better sample efficiency, unstable
3. SAC: stochastic policies + replay buffer + entropy regularization, stable and sample efficient
   

stochastic policies: 这是指实际执行的动作是对概率分布采样得到的，因为TRPO and PPO都是AC框架下的产物，其执行的动作取决于输出策略网络的概率分布的采样。

deterministic policies：可以通过网络给每个动作的打分，通过贪婪策略选定最高打分的动作执行。

on-policy&off-policy：on-policy就是采样的数据和某个策略强绑定，也就是采样的数据只能用于某个策略的训练，策略更新后原来的数据就没用了。off-policy就是采样得到的数据可以拿来训练所有的网络，因此采样可以被看做一个单独的任务。
重要性采样是无法改变其on-policy的本质的，像PPO算法，虽然有2个policy，用pi_old采样去更新pi，但是由于pi_old的参数是从pi复制的，本质上还是属于同一个策略（重要性采样的前提就是策略pi_old和策略pi比较接近）。所以PPO是一个看起来很像off-policy的on-policy算法。
此外，另一个直接的解释就是重要性采样只能让网络使用同一组数据去多次训练，而无法像off-policy的方法那样直接把轨迹数据存memory_buffer里面然后随机抽样（可以参考上面的DQN和PPO的实现）。

replay buffer：按照上面的说法，正常是off-policy的方法才能使用replay buffer，但是重要性可以让on-policy的算法也能replay。区别是off-policy的replay buffer能把轨迹数据存memory_buffer里面然后随机抽样。但是on-policy的replay只能让网络使用同一组数据多次迭代而已，多次迭代完原来的数据要全部扔掉重新采样。

entropy regularization：SAC考虑了熵，探索性更强。

1、基本参数定义

Reward：奖励R，每次（每一步）与环境进行交互都会获得奖励，玩一整局，奖励的和自然是越多越好。

Q(s,a)：动作价值函数，其输入为当前状态和要执行的动作，输出为该动作能带来多大的价值，因此，一种贪心的方法是选择能够使Q(s,a)最大动作执行。
$$Q_{\pi }(s_t,a_t)=\mathbb{E}{s}_{t+1},a_{t+1},\dots \left[\sum _{l=0}^{\infty }{\gamma }^{l}r(s_{t+l})\right]$$
Q(s,a)的维度等于动作空间的维度。打个简单的比方，假设我现在有两个动作，向北去捡芝麻，向南去捡西瓜。从最终获得的奖励来看，西瓜是大于芝麻的，但是如果芝麻就在我桌上，但是西瓜在20km以外，那可能我还是选择芝麻得了。那么动作价值函数可能就是（1，0.1）。1是捡芝麻的动作价值，0.1是捡西瓜的动作价值，虽说西瓜好吃，但是太远了，所以其动作价值打分特别低。

V(s)：状态价值函数，是Q函数的期望。因为期望的积分动作消去了动作A，因此状态价值函数V可以用来直观的反应一个状态的好坏。其实际上是Q(s,a)对不同a的加权平均。
例如，自家高低三路被破，依据这个状态我们就知道现在的状态打分不太行。状态打分不行的原因是每个动作都不会带来太高的打分（都要输了）。
$$V_{\pi }(s_t)={\mathbb{E}}_{A_t}[Q_{\pi }(s_t,A_t)\mid s_t]$$

A：优势函数，其数值等于动作价值函数减去状态价值函数，相当于动作价值Q(s,a)减去了其baseline：
$$A_{\pi }(s,a)=Q_{\pi }(s,a)?V_{\pi }(s)$$

2、SAC基础思路

2.1、考虑熵的Policy网络

13、近端策略优化Proximal Policy Optimization (PPO) 算法：从原理到实践中介绍了基础的AC框架，其中Actor网络的目标函数为：
$$J(\theta )=E_{\tau ～p_{\theta }(\tau )}\left[\sum _{t}r({\mathbf{s}}_t,{\mathbf{a}}_t)\right]\approx \frac{1}{N}\sum _i\sum _{t}r({\mathbf{s}}_{i,t},{\mathbf{a}}_{i,t})$$

在SAC中，对式子进行了修改，考虑了熵来增加其探索性：
$$J(\pi )=\sum _{t=0}^T{\mathbb{E}}_{({\mathbf{s}}_t,{\mathbf{a}}_t)～{\rho }_{\pi }}\left[r({\mathbf{s}}_t,{\mathbf{a}}_t)+\alpha \mathcal{H}(\pi (?|{\mathbf{s}}_t))\right]$$
其中$\alpha$是温度系数，这个参数可以是自己确定的超参数，作者也给出了自适应的计算方法，在后面会提及。

2.2、考虑熵的Critic网络(Soft Policy Evaluation)

首先需要了解贝尔曼方程：
$$Q(s,a)=r(s)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s)V(s^{\prime })=r(s)+\gamma {\mathbb{E}}_{{\mathbf{s}}_{t+1}～p}\left[V({\mathbf{s}}_{t+1})\right]$$
对其考虑熵，定义一个考虑熵的Q(s,a)为${\mathcal{T}}^{\pi }Q({\mathbf{s}}_t,{\mathbf{a}}_t)$：
$${\mathcal{T}}^{\pi }Q({\mathbf{s}}_t,{\mathbf{a}}_t)?r({\mathbf{s}}_t,{\mathbf{a}}_t)+\gamma {\mathbb{E}}_{{\mathbf{s}}_{t+1}～p}\left[V({\mathbf{s}}_{t+1})\right]$$
其中：
$$V({\mathbf{s}}_t)={\mathbb{E}}_{{\mathbf{a}}_t～\pi }\left[Q({\mathbf{s}}_t,{\mathbf{a}}_t)?\log \pi ({\mathbf{a}}_t|{\mathbf{s}}_t)\right]$$
为什么$V({\mathbf{s}}_t)$写成这个形式呢，那就得看看熵的计算公式了：
$$H(X)=?\sum _{i=1}^{n}p\left(x_i\right)\log p\left(x_i\right)=E(?\log p\left(x\right))$$
因此，上面的$V({\mathbf{s}}_t)$实际上就是Q的期望加上H(X)。然而，对于修改后的式子${\mathcal{T}}^{\pi }Q({\mathbf{s}}_t,{\mathbf{a}}_t)?r({\mathbf{s}}_t,{\mathbf{a}}_t)+\gamma {\mathbb{E}}_{{\mathbf{s}}_{t+1}～p}\left[V({\mathbf{s}}_{t+1})\right]$，如何证明其仍然收敛呢，证明过程参考SAC: Soft Actor-Critic Part 1的14min22s。

2.3、Soft Policy lmprovement

使用价值函数进行学习的算法(如DQN等等)，可以根据动作价值函数对每个动作的打分来进行实际的动作选取。

如果对其进行归一化使得对所有动作的打分和为1，那么价值网络输出的也可以被视为一个概率分布了。SAC的Actor进行Soft Policy lmprovement的关键就是让策略网络的输出（Softmax）去逼近价值网络输出的Q（需要归一化成一个概率分布的形式），其公式形如：
$${\pi }_{\mathrm{new}}=\arg \underset{{\pi }^{\prime }\in \Pi }{\min }{\mathrm{D}}_{\mathrm{KL}}({\pi }^{\prime }(?|{\mathbf{s}}_t)\Vert \frac{\exp \left(Q^{{\pi }_{\mathrm{old}}}({\mathbf{s}}_t,?)\right)}{Z^{{\pi }_{\mathrm{old}}}({\mathbf{s}}_t)})$$

作者证明，只要动作空间有限，更新可以使得新的方法表现更好：
$$Q^{{\pi }_{\mathrm{new}}}({\mathbf{s}}_t,{\mathbf{a}}_t)\ge Q^{{\pi }_{\mathrm{old}}}({\mathbf{s}}_t,{\mathbf{a}}_t)$$
证明过程见：SAC: Soft Actor-Critic Part 1的17min20s

2.4、Soft Policy Iteration

结合2.2 Soft Policy Evaluation和2.3 Soft Policy lmprovement，作者证明，通过这两个迭代，最终的效果会越来越好：

证明过程见：SAC: Soft Actor-Critic Part 1的22min25s。

3、Soft Actor Critic网络框架与更新

综上，Soft Actor Critic一共需要用到3种网络，分别是状态价值网络V，动作价值网络Q，策略网络pi。
经典：需要一个V网络，一个Target-V网络；两个Q网络（加速迭代）；一个策略网络
SAC升级版：2 Q net, 2 target Q net, 1 policy net

3.1 状态价值函数V的更新（Soft value functon update）

状态价值函数V的更新依赖于2.2中介绍的公式：
$$V({\mathbf{s}}_t)={\mathbb{E}}_{{\mathbf{a}}_t～\pi }\left[Q({\mathbf{s}}_t,{\mathbf{a}}_t)?\log \pi ({\mathbf{a}}_t|{\mathbf{s}}_t)\right]$$
其更新的目标函数是上式做差的平方的一半，具体来讲就是均方误差函数：
$$J_V(\psi )={\mathbb{E}}_{{\mathbf{s}}_t～\mathcal{D}}\left[\frac{1}{2}{\left(V_{\psi }({\mathbf{s}}_t)?{\mathbb{E}}_{{\mathbf{a}}_t～{\pi }_{?}}\left[Q_{\theta }({\mathbf{s}}_t,{\mathbf{a}}_t)?\log {\pi }_{?}({\mathbf{a}}_t|{\mathbf{s}}_t)\right]\right)}^2\right]$$

此外，在经典的SAC算法中，还有一个target-V网络，这个是用来进行Target-Q的计算的。target-V网络基于V网络进行软更新得到的。
参考07、基于LunarLander登陆器的DQN强化学习案例（含PYTHON工程）里面的1.2软更新（Soft Updates）

基本代码（状态价值函数V的更新）：

target_value_func = predicted_new_q_value - alpha * log_prob  # for stochastic training, it equals to expectation over action
value_criterion = nn.MSELoss()
value_loss = value_criterion(predicted_value, target_value_func.detach())

基本代码（V-target的软更新）：

# Soft update the target value net
for target_param, param in zip(target_value_net.parameters(), value_net.parameters()):
    target_param.data.copy_(  # copy data value into target parameters
        target_param.data * (1.0 - soft_tau) + param.data * soft_tau
    )

在一些更新版本的SAC代码中，没有V网络直接用Q网络代替，这样被证实效果更好。

3.2 动作价值函数Q的更新（Soft Q functon update）

动作价值函数Q的更新和DQN的基本差不多，也就是用Q网络和Target-Q来进行更新。参考07、基于LunarLander登陆器的DQN强化学习案例（含PYTHON工程）

由此，Q网络的更新是用Q去逼近Target-Q，如：
$$J_Q(\theta )={\mathbb{E}}_{({\mathbf{s}}_t,{\mathbf{a}}_t)～\mathcal{D}}\left[\frac{1}{2}{\left(Q_{\theta }({\mathbf{s}}_t,{\mathbf{a}}_t)?\hat{Q}({\mathbf{s}}_t,{\mathbf{a}}_t)\right)}^2\right]$$
但是，和DQN这类算法不同的是，经典的SAC算法的Target-Q并非是基于网络得出，而是基于贝尔曼方程：
$$\hat{Q}({\mathbf{s}}_t,{\mathbf{a}}_t)=r({\mathbf{s}}_t,{\mathbf{a}}_t)+\gamma {\mathbb{E}}_{{\mathbf{s}}_{t+1}～p}\left[\hat{V}({\mathbf{s}}_{t+1})\right]$$

在实际运用中，我们往往使用两个Q网络（选择较小的Q来进行计算），这样会加快训练的速度。

    predicted_q_value1 = soft_q_net1(state, action)
    predicted_q_value2 = soft_q_net2(state, action)
    q_value_loss1 = soft_q_criterion1(predicted_q_value1, target_q_value.detach())  # detach: no gradients for the variable
    q_value_loss2 = soft_q_criterion2(predicted_q_value2, target_q_value.detach())
	......
    soft_q_optimizer1.zero_grad()
    q_value_loss1.backward()
    soft_q_optimizer1.step()
    soft_q_optimizer2.zero_grad()
    q_value_loss2.backward()
    soft_q_optimizer2.step()
	......
	predicted_new_q_value = torch.min(soft_q_net1(state, new_action), soft_q_net2(state, new_action))

3.3 策略网络的更新（Soft policy functon update）与重参数思想

2.3、Soft Policy lmprovement中提到，策略网络的更新是让其接近动作价值函数Q的输出分布：
$$J_{\pi }(?)={\mathbb{E}}_{{\mathbf{s}}_t～\mathcal{D}}\left[{\mathrm{D}}_{\mathrm{KL}}({\pi }_{?}(?|{\mathbf{s}}_t)\Vert \frac{\exp \left(Q_{\theta }({\mathbf{s}}_t,?)\right)}{Z_{\theta }({\mathbf{s}}_t)}\right)]$$

在传统的策略梯度法中，我们往往将梯度写成期望形式，并用似然函数与蒙特卡洛来进行计算：
$${?}_{\theta }J(\theta )=\int \underbrace{{?}_{\theta }{p}_{\theta }(\tau )}r(\tau )d\tau =\int p_{\theta }(\tau ){?}_{\theta }\log p_{\theta }(\tau )r(\tau )d\tau =E_{\tau ～p_{\theta }(\tau )}[{?}_{\theta }\log p_{\theta }(\tau )r(\tau )]$$

一旦使用了这种方法，那么采样的数据和某个策略强绑定，训练就变成了on-policy的形式了。在SAC算法中，我们使用了重参数的思想，就是我们只从策略网络得到分布的均值和方差，然后使用均值和方差构建一个独立的高斯分布，这样就保证了分布和网络的独立性（tanh来限制范围）：
$$\begin{array}{rl}a=\tanh ({\mu }_{?}+?{\sigma }_{?})& \text{?where?}?～\mathcal{N}(0,1)\end{array}$$
证明过程见：SAC: Soft Actor-Critic Part 1的28min55s。
在代码中，policy网络的构建可以不再使用softmax来输出分布，而是直接输出均值和方差（参考Policy网络的forward函数）：

def forward(self, state):
    x = self.activation(self.linear1(state))
    x = self.activation(self.linear2(x))
    x = self.activation(self.linear3(x))
    x = self.activation(self.linear4(x))

    mean = (self.mean_linear(x))
    # mean    = F.leaky_relu(self.mean_linear(x))
    log_std = self.log_std_linear(x)
    log_std = torch.clamp(log_std, self.log_std_min, self.log_std_max)

    return mean, log_std

在模型的evaluate中，我们使用方差和均值来重新构造分布，并得到要执行的action 与分布函数：

    def evaluate(self, state, epsilon=1e-6):
        '''
        generate sampled action with state as input wrt the policy network;
        deterministic evaluation provides better performance according to the original paper;
        '''
        mean, log_std = self.forward(state)
        std = log_std.exp()  # no clip in evaluation, clip affects gradients flow

        normal = Normal(0, 1)
        z = normal.sample(mean.shape)
        action_0 = torch.tanh(mean + std * z.to(device))  # TanhNormal distribution as actions; reparameterization trick
        action = self.action_range * action_0
        ''' stochastic evaluation '''
        log_prob = Normal(mean, std).log_prob(mean + std * z.to(device)) - torch.log(
            1. - action_0.pow(2) + epsilon) - np.log(self.action_range)
        ''' deterministic evaluation '''
        # log_prob = Normal(mean, std).log_prob(mean) - torch.log(1. - torch.tanh(mean).pow(2) + epsilon) -  np.log(self.action_range)
        '''
         both dims of normal.log_prob and -log(1-a**2) are (N,dim_of_action); 
         the Normal.log_prob outputs the same dim of input features instead of 1 dim probability, 
         needs sum up across the features dim to get 1 dim prob; or else use Multivariate Normal.
         '''
        log_prob = log_prob.sum(dim=-1, keepdim=True)
        return action, log_prob, z, mean, log_std

此外，一番推导，我们可以得到Policy网络在重参数下的更新方程（证明过程见：SAC: Soft Actor-Critic Part 1的36min。）：
$$\begin{array}{r}{J}_{\pi }(?)={\mathbb{E}}_{{\mathbf{s}}_t～\mathcal{D},{?}_t～\mathcal{N}}\left[\log {\pi }_{?}(f_{?}({?}_t;{\mathbf{s}}_t)|{\mathbf{s}}_t)?Q_{\theta }({\mathbf{s}}_t,f_{?}({?}_t;{\mathbf{s}}_t))\right]\end{array}$$

作为对照，其编程实现为：

policy_loss = (log_prob - predicted_new_q_value).mean()

3.4 决策边界Bound

参考SAC: Soft Actor-Critic Part 1的38min40s。
由于我们的动作的采样是基于高斯分布的，因此会有较小的概率采样到非常离谱的值，因此需要加tau函数进行限制，因此似然估计需要变成：
$$\log \pi (\mathbf{a}|\mathbf{s})=\log \mu (\mathbf{u}|\mathbf{s})?\sum _{i=1}^D\log \left(1?{\tanh }^2(u_i)\right)$$

因此，仔细观察上面的evaluate：

log_prob = Normal(mean, std).log_prob(mean + std * z.to(device)) - torch.log(
    1. - action_0.pow(2) + epsilon) - np.log(self.action_range)

其中Normal(mean, std).log_prob(mean + std * z.to(device))是采样的数据，- torch.log(
1. - action_0.pow(2) + epsilon)对应于决策边界Bound，而- np.log(self.action_range)是对动作空间进行归一化（可以和第一项一起看，写成Normal(mean, std).log_prob(mean + std * z.to(device))- np.log(self.action_range)）。

4、自动确定温度系数$\alpha$

在SAC中，对式子进行了修改，考虑了熵来增加其探索性：
$$J(\pi )=\sum _{t=0}^T{\mathbb{E}}_{({\mathbf{s}}_t,{\mathbf{a}}_t)～{\rho }_{\pi }}\left[r({\mathbf{s}}_t,{\mathbf{a}}_t)+\alpha \mathcal{H}(\pi (?|{\mathbf{s}}_t))\right]$$

但是，其中温度系数$\alpha$需要手动进行确定，是一个超参数。在升级版本中，作者给出了一个自动确定$\alpha$的方法，如下（推导见SAC: Soft Actor-Critic Part 2）：
$${\alpha }_t^{?}=\arg \underset{{\alpha }_t}{\min }{\mathbb{E}}_{{\mathbf{a}}_t～{\pi }_t^{?}}\left[?{\alpha }_t\log {\pi }_t^{?}({\mathbf{a}}_t|{\mathbf{s}}_t;{\alpha }_t)?{\alpha }_t\bar{\mathcal{H}}\right]$$

这实际是一个迭代式子，因此使用梯度下降进行优化：
定义：

self.log_alpha = torch.zeros(1, dtype=torch.float32, requires_grad=True, device=device)
alpha_lr = 3e-4
self.alpha_optimizer = optim.Adam([self.log_alpha], lr=alpha_lr)
self.alpha = self.log_alpha.exp()

梯度下降：

# Updating alpha wrt entropy
# alpha = 0.0  # trade-off between exploration (max entropy) and exploitation (max Q)
if auto_entropy is True:
    alpha_loss = -(self.log_alpha * (log_prob + target_entropy).detach()).mean()
    # print('alpha loss: ',alpha_loss)
    self.alpha_optimizer.zero_grad()
    alpha_loss.backward()
    self.alpha_optimizer.step()

5. 基于LunarLander登陆器的Soft Actor-Critic强化学习

代码参考最上方链接。
效果真的是乱杀啊：

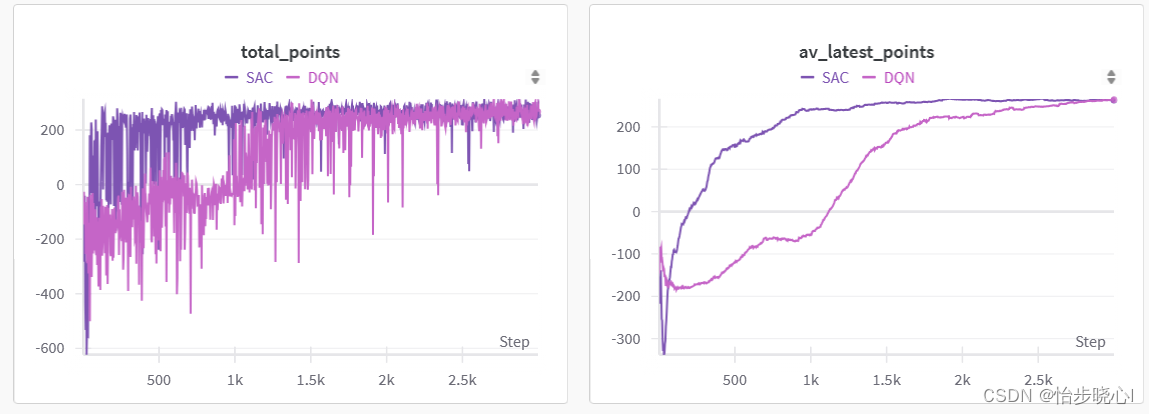
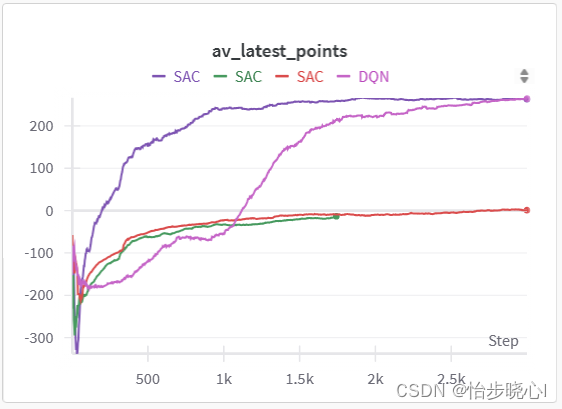
但是，并不是每次训练都有好的效果，如果一开始没有学习到好的策略，后来其学习也会非常乏力：