代码随想录算法训练营第25天 | 216.组合总和III 17.电话号码的字母组合

目录

216.组合总和III

💡解题思路

回溯三部曲

💻实现代码

17.电话号码的字母组合

💡解题思路

# 数字和字母如何映射

# 回溯法来解决n个for循环的问题

💻实现代码

---

216.组合总和III

题目链接：216.组合总和III

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

• 所有数字都是正整数。
• 解集不能包含重复的组合。

示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]]

示例 2: 输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]]

💡解题思路

回溯三部曲

• 确定递归函数参数

和77.组合一样，依然需要一维数组path来存放符合条件的结果，二维数组result来存放结果集。

这里我依然定义path 和 result为全局变量。

至于为什么取名为path？从上面树形结构中，可以看出，结果其实就是一条根节点到叶子节点的路径。

vector<vector<int>> result; // 存放结果集
vector<int> path; // 符合条件的结果

接下来还需要如下参数：

• targetSum（int）目标和，也就是题目中的n。
• k（int）就是题目中要求k个数的集合。
• sum（int）为已经收集的元素的总和，也就是path里元素的总和。
• startIndex（int）为下一层for循环搜索的起始位置。

所以代码如下：

vector<vector<int>> result;
vector<int> path;
void backtracking(int targetSum, int k, int sum, int startIndex)

其实这里sum这个参数也可以省略，每次targetSum减去选取的元素数值，然后判断如果targetSum为0了，说明收集到符合条件的结果了，我这里为了直观便于理解，还是加一个sum参数。

还要强调一下，回溯法中递归函数参数很难一次性确定下来，一般先写逻辑，需要啥参数了，填什么参数。

• 确定终止条件

什么时候终止呢？

在上面已经说了，k其实就已经限制树的深度，因为就取k个元素，树再往下深了没有意义。

所以如果path.size() 和 k相等了，就终止。

如果此时path里收集到的元素和（sum） 和targetSum（就是题目描述的n）相同了，就用result收集当前的结果。

所以 终止代码如下：

if (path.size() == k) {
    if (sum == targetSum) result.push_back(path);
    return; // 如果path.size() == k 但sum != targetSum 直接返回
}

💻实现代码

class Solution {
    List<List<Integer>> res =new ArrayList<>();
    LinkedList<Integer> path =new LinkedList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
        backtracking(k,n,1,0);
        return res;
    }
    private void backtracking(int k,int n,int startIndex,int sum){
        if(sum>n) return;
        if(path.size()==k){
            if(sum==n){
                res.add(new ArrayList<>(path));
                return;
            }    
        }
        for(int i=startIndex;i<=9-(k-path.size())+1;i++){
            path.add(i);
            sum+=i;
            backtracking(k,n,i+1,sum);
            path.removeLast();
            sum-=i;
        }
    }
}

17.电话号码的字母组合

题目链接： 17.电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例:

• 输入："23"
• 输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

说明：尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

💡解题思路

理解本题后，要解决如下三个问题：

1. 数字和字母如何映射
2. 两个字母就两个for循环，三个字符我就三个for循环，以此类推，然后发现代码根本写不出来
3. 输入1 * #按键等等异常情况

# 数字和字母如何映射

可以使用map或者定义一个二维数组，例如：string letterMap[10]，来做映射，我这里定义一个二维数组，代码如下：

const string letterMap[10] = {
    "", // 0
    "", // 1
    "abc", // 2
    "def", // 3
    "ghi", // 4
    "jkl", // 5
    "mno", // 6
    "pqrs", // 7
    "tuv", // 8
    "wxyz", // 9
};

# 回溯法来解决n个for循环的问题

例如：输入："23"，抽象为树形结构，如图所示：

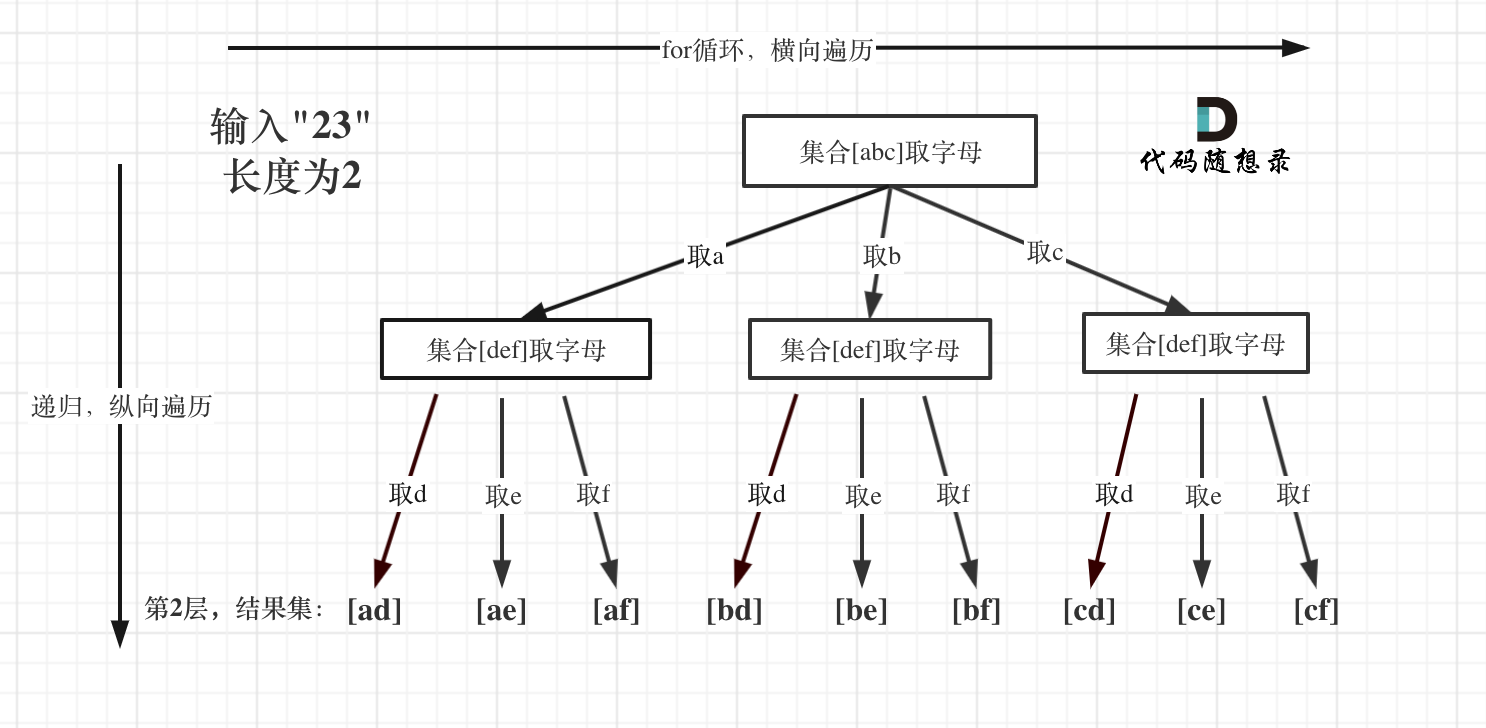
图中可以看出遍历的深度，就是输入"23"的长度，而叶子节点就是我们要收集的结果，输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。

回溯三部曲：

• 确定回溯函数参数

首先需要一个字符串s来收集叶子节点的结果，然后用一个字符串数组result保存起来，这两个变量我依然定义为全局。

再来看参数，参数指定是有题目中给的string digits，然后还要有一个参数就是int型的index。

注意这个index是记录遍历第几个数字了，就是用来遍历digits的（题目中给出数字字符串），同时index也表示树的深度。

代码如下：

vector<string> result;
string s;
void backtracking(const string& digits, int index)

• 确定终止条件

例如输入用例"23"，两个数字，那么根节点往下递归两层就可以了，叶子节点就是要收集的结果集。

那么终止条件就是如果index 等于 输入的数字个数（digits.size）了（本来index就是用来遍历digits的）。

然后收集结果，结束本层递归。

代码如下：

if (index == digits.size()) {
    result.push_back(s);
    return;
}

• 确定单层遍历逻辑

首先要取index指向的数字，并找到对应的字符集（手机键盘的字符集）。

然后for循环来处理这个字符集，代码如下：

int digit = digits[index] - '0';        // 将index指向的数字转为int
string letters = letterMap[digit];      // 取数字对应的字符集
for (int i = 0; i < letters.size(); i++) {
    s.push_back(letters[i]);            // 处理
    backtracking(digits, index + 1);    // 递归，注意index+1，一下层要处理下一个数字了
    s.pop_back();                       // 回溯
}

💻实现代码

class Solution {
    List<String> list=new ArrayList<>();
    public List<String> letterCombinations(String digits) {
        if(digits==null ||digits.length()==0){
            return list;
        }
        String[] str= {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
        backtracking(digits,str,0);
        return list;
    }
    StringBuilder sb=new StringBuilder();
    private void backtracking(String digits,String[] str,int num){
        if(num==digits.length()){
            list.add(sb.toString());
            return;
        }
        String s = str[digits.charAt(num) - '0'];
        for(int i=0;i<s.length();i++){
            sb.append(s.charAt(i));
            backtracking(digits,str,num+1);
            sb.deleteCharAt(sb.length()-1);
        }
    }
}