Linux内核之红黑树详解（1）

1、红黑树的定义：

红黑树，又称为Red-Black Tree 「RBT」是一个自平衡(不是绝对的平衡)的二叉查找树(BST)。红黑树是一种特化的AVL树（平衡二叉树），都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的： 它可以在O(log n)时间内做查找，插入和删除，这里的n 是树中元素的数目。

2、红黑树的性质（规则）：

红黑树是一种含有红黑节点并能自平衡的二叉查找树。它必须满足下面的性质：

a、性质1：每个结点要么是黑色，要么是红色；

b、性质2：根节点是黑色；

c、性质3：每个叶子结点（NIL）是黑色；

d、性质4：每个红色结点的两个子结点一定都是黑色（不能有两个连续的红色结点）；

e、性质5：任意一结点到每个叶子结点的路径都包含数量相同的黑结点（尽量保证这棵树是平衡的）。

3、红黑树的自平衡操作：

红黑树依靠三种操作进行自平衡，分别为：左旋、右旋、变色。

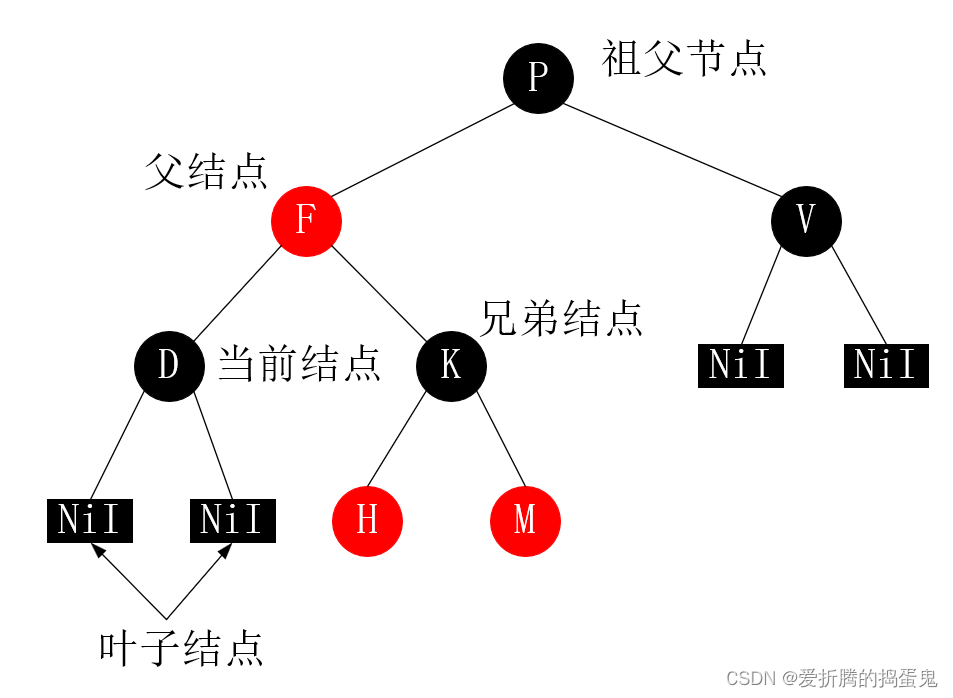
正在处理的结点被称为当前结点，它的父亲被称为父结点，它父亲的另一个子结点被称为兄弟结点，父亲的父亲被称为祖父结点。则红黑树的自平衡处理可以被总结为：

自己能够解决的就自我消化；自己搞不定的先找兄弟帮忙；兄弟也搞不定的，找父母和远房亲戚帮忙。

4、红黑树的基本实现：

a、结构定义：

#define RED        0    			// 红色节点
#define BLACK    1    				// 黑色节点

typedef int Type;

// 红黑树的节点
typedef struct RBTreeNode{
    unsigned char color;        	// 颜色(RED 或 BLACK)
    Type   key;                     // 关键字(键值)
    struct RBTreeNode *left;    	// 左孩子
    struct RBTreeNode *right;    	// 右孩子
    struct RBTreeNode *parent;    	// 父结点
}Node, *RBTree;

// 红黑树的根
typedef struct rb_root{
    Node *node;
}RBRoot;

红黑树可以进行添加、删除和旋转。红黑树在进行添加和删除之后，就会进行旋转。因为在添加和删除红黑树中的结点之后，就会破坏红黑树的一些性质，使得红黑树转变成一颗普通的树，通过旋转就可以使得这棵树重新成为红黑树。旋转包括左旋和右旋两种。

b、左旋：

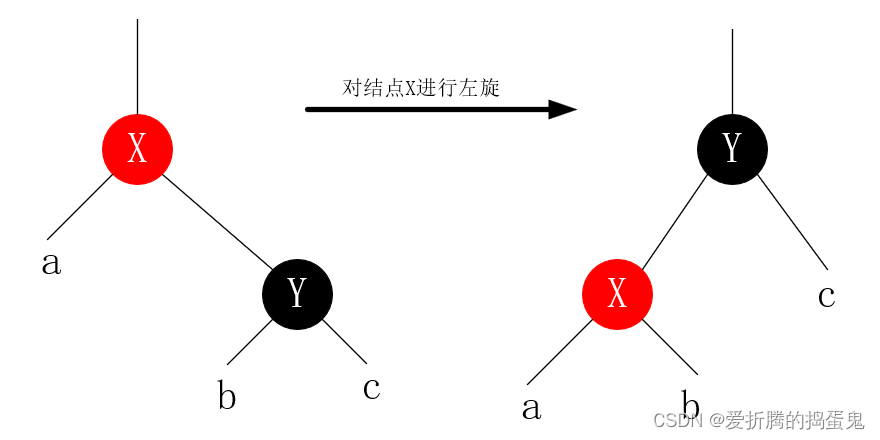
左旋的C语言实现：

/* 
 * 对红黑树的节点(x)进行左旋转
 * 左旋示意图(对节点x进行左旋)：
 *      p                              p
 *     /                               /
 *    x                               y                
 *   /  \      --(左旋)-->           / \                
 *  lx   y                          x  ry     
 *     /   \                       /  \
 *    ly   ry                     lx  ly  
 */
static void rbtree_left_rotate(RBRoot *root, Node *x)
{

    Node *y = x->right;    		   // 设置x的右孩子为y
 
    x->right = y->left;				// 将 “y的左孩子” 设为 “x的右孩子”；
    if (y->left != NULL)
        y->left->parent = x;		// 如果y的左孩子非空，将 “x” 设为 “y的左孩子的父亲”

    y->parent = x->parent;			// 将 “x的父亲” 设为 “y的父亲”
    if (x->parent == NULL)
    {
        root->node = y;             // 如果 “x的父亲” 是空节点，则将y设为根节点
    }
    else
    {
        if (x->parent->left == x)
            x->parent->left = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
        else
            x->parent->right = y;   // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
    } 
    y->left = x;					// 将 “x” 设为 “y的左孩子”
    x->parent = y;					// 将 “x的父节点” 设为 “y”
}

c、右旋：

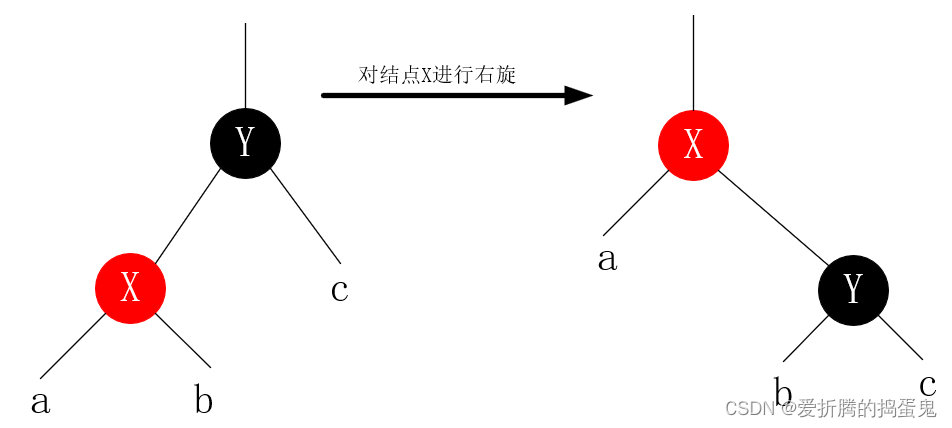
右旋的C语言实现：

/* 
 * 对红黑树的节点(y)进行右旋转
 * 右旋示意图(对节点y进行左旋)：
 *            p                               p
 *           /                                /
 *          y                                x                  
 *         /  \      --(右旋)-->            /  \                     
 *        x   ry                           lx   y  
 *       / \                                   / \                   
 *      lx  rx                                rx  ry
 */
static void rbtree_right_rotate(RBRoot *root, Node *y)
{
    
    Node *x = y->left;				// 设置x是当前节点的左孩子。
   
    y->left = x->right;				// 将 “x的右孩子” 设为 “y的左孩子”；
    if (x->right != NULL)
        x->right->parent = y;		// 如果"x的右孩子"不为空的话，将 “y” 设为 “x的右孩子的父亲”

    x->parent = y->parent;			// 将 “y的父亲” 设为 “x的父亲”
    if (y->parent == NULL) 
    {
        root->node = x;         	// 如果 “y的父亲” 是空节点，则将x设为根节点
    }
    else
    {
        if (y == y->parent->right)
            y->parent->right = x;    // 如果 y是它父节点的右孩子，则将x设为“y的父节点的右孩子”
        else
            y->parent->left = x;     // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”
    }
    x->right = y; 					// 将 “y” 设为 “x的右孩子”
    y->parent = x;					// 将 “y的父节点” 设为 “x”
}