【论文解读】Early Skip Mode Decision for HEVC Encoder With Emphasis on Coding Quality
时间:2015
级别:IEEE
机构:IEEE 学生会员
摘要
高效视频编码(High Efficiency Video Coding, HEVC)以其较高的压缩效率和良好的编码图像质量适用于高清和超高清视频业务,但其较高的编码复杂度阻碍了其广泛的实际应用。许多快速编码方案虽然可以缓解复杂度问题,但其编码质量受到较大影响。提出了一种早期的skip模式选择策略,在不牺牲HEVC编码质量的前提下,降低了HEVC的编码复杂度。该方法在计算2N×2N合并模式的率失真代价后,利用其失真特性确定skip模式,而被判定为skip模式的预测单元不进行剩余模式的决策过程。早期判决阈值直接从视频数据本身估计。实验结果表明,与HEVC全率失真优化判决相比,该方法在几乎没有编码损失的情况下,在随机接入主条件下平均降低30.1%的编码复杂度,在低时延主条件下平均降低26.4%的编码复杂度。
介绍
电视广播、网络视频甚至移动应用对高分辨率多媒体服务的需求已经迫在眉睫。为了满足这一需求,ITU-R对超高清(UHD)电视提出了新的建议,包括4K或8K分辨率。超高清业务的视频数据量巨大,对传输带宽提出了更高的要求,因此需要一种比H.264/MPEG-4 AVC更强大的视频编码技术。MPEG- h第2部分(ISO/IEC 23008-2)/ITU-T H.265(又称HEVC (High Efficiency Video Coding))是ISO/IEC MPEG和ITU-T VCEG为满足这一需求而制定的最新的视频编码标准。与H.264/ MPEG-4 AVC相比,该算法在保证同等视频质量的前提下,码率降低了50%。算法采用了更大的块尺寸、灵活的编码单元(CU)、预测单元(PU)、变换单元(TU)、更先进的运动矢量编码、样本自适应偏移(SAO)和非对称运动划分(AMP)等先进的编码工具。在HEVC中,一幅图像或一个片被分割成多个编码树单元(CTU),其功能与H.264/MPEG-4 AVC中的宏块相同。它的大小由一个编码器选择,从16×16到64×64,包括。一个CTU可以递归地划分为四个四叉树块,四叉树中的每个终端块称为CU。最小CU不能小于用户特定或16×16,以较大的为准。预测类型,即帧内预测或帧间预测,在CU层面决定。根据预测类型的不同,CU可以被划分为多个预测单元(PU)。在帧内模式下只允许2N×2N和N×N PUs,在帧间模式下支持各种PU大小,如2N×2N, 2N×N, N×2N, N×N和AMP PUs。在确定合适的预测模式后,有选择地对预测产生的残差进行变换。与H.264/MPEG-4 AVC相比,不同的变换大小(从4×4到32×32)可以在CU中编码残差。为了确定一个CTU的CU、PU和TU结构的最佳组合,HEVC编码器通常对所有CU、PU和TU的候选组合结构进行运动估计、模式选择和变换过程,虽然HEVC采用非常灵活的结构获得了良好的编码效率,但其编码的计算复杂度明显高于传统的视频编码标准H.264/MPEG-4 AVC。由于超高清业务对编码质量非常敏感,在保证编码质量的前提下降低编码复杂度显得尤为重要。
目前已经有几种降低HEVC编码计算复杂度的方法,例如CU深度的提前确定、模式选择过程的提前终止以及残差四叉树变换(RQT)深度的快速决策。Choi等人提出的早期CU深度决策在当前CU的最优预测模式为skip时,利用预测模式信息终止剩余CU决策过程。Z. Liu等利用先前图片中相邻CU和并置CU的深度等级来确定CU的深度范围。Cho和Kim提出了一种基于率失真(rate-distortion, RD)代价和全模式代价的帧内CU深度决策方法。当当前PU类型的量化残差为零时,Gweon和Lee终止剩余PU决策过程。Yang等人和Kim等人将H.264/MPEG-4 AVC中的早期跳过模式选择方法扩展到HEVC中。
当2N×2N PU的运动矢量差为零且其量化残差均为零时,确定跳跃模式。为了决定跳跃模式,执行2N×2N PU(即2N×2N AMVP(高级运动矢量预测)过程)的运动估计。Pan等人提出了一种利用运动估计信息和全零块信息的早期合并模式决策方法。Choi和Jang在当前TU的非零变换系数小于3时终止RQT深度决策过程。但这些方法无论编码质量大小,都存在一定程度的编码质量损失。其他方法与快速HEVC编码器的早期跳过模式决策有关。Goswami等人识别出当前帧中的静止区域和均匀区域,并将其选择为跳跃区域。Choi等利用当前帧中相邻且已编码的skip PU预测当前2Nx2N PU的skip RD代价,并将其与当前PU的skip模式实际RD 代价进行比较。尽管这些方法比[11]和[12]节省了稍多的时间,但它们仍然有相当大的编码质量损失。
提出了一种快速HEVC编码器的早期跳过模式选择方法,特别强调了最小化编码损失的影响。这对于超高清(UHD)业务,或者对编码质量要求非常高的编码应用来说,是非常重要的。所提出的快速方法被设计为尽可能简单,通过将其实现为一个简单的阈值过程-当2N×2N合并模式的失真小于给定阈值时,它终止剩余模式的决策过程。该方法的一个重要特点是其阈值直接由skip PUs的失真特性估计而来,因此无需用户提供。
skip 模式的特性
为了使HEVC编码器基于率失真优化来决定最优的预测模式,计算每个预测模式的RD代价J,并选择RD代价最小的预测模式。RD 代价的计算方法如下:

其中D是当前预测模式的失真值,R是表示压缩比特流中残差及其模式信息的比特代价,λ是对应于QP(量化参数)的拉格朗日乘子。HEVC参考SW采用当前主用户与其重构块之间的误差平方和(SSE)来测量失真度D。
HEVC解码器将skip模式解释为PU大小为2N×2N,其预测模式为merge,并且没有发送与PU相关的残差变换系数(可以是它们都真正量化为零,或者它们不简单发送)。这三个条件作为一个整体被称为跳过条件(skip condition)。由于跳过模式是编码器向解码器发送编码决策信号的一种方式,因此编码器可以自己决定跳过模式,而不管特定Merge候选的跳过条件是否满足,只要这样的决定在RD意义上更好。例如,即使特定的候选Merge满足条件,如果某些其他编码模式产生的失真远远小于补偿增加的速率代价(例如,通过显式发送运动矢量和参考图像索引),编码器会选择其他模式(让我们称之为情况A)。在同一个token中,即使任何一个候选Merge不满足跳过条件,如果一个特定的Merge候选的失真非常小,甚至没有发送任何残差信息(即,当没有向解码器发送量化残差信号时),编码器可以选择PU作为Skip模式(我们称之为情况B)。因此,当某个特定的候选Merge满足跳过条件时,如果不对其他模式进行进一步的详尽测试,就立即决定跳过模式,这可能是有害的,如图1所示,图1显示了两种情况的平均SSE值。一种是当前CU的最终最优预测模式为Skip时(图1中灰色或黄色)。注意,这种情况下的SSE值通常都很低。另一种情况(如图1中黑色或蓝色所示),即使满足跳过条件,最终的最优模式也不是Skip 模式。注意,这种情况下的SSE值比前一种情况大得多。由于 Skip模式的SSE值取决于PU大小(从64×64到8×8),因此图1中的SSE值归一化为8×8 PU大小。如图1所示,尽管当前CU(如2N×2N PU)满足跳过条件,但如果其失真(即SSE)相对较大,其最终的RD最优预测模式可能不是Skip模式。它描述了之前讨论过的案例A。为了更准确地及早决定Skip模式,同时最小化相应的编码损失,图1建议我们,除了 跳过条件外,还要检查失真是否足够低。它让快速编码器避免了情况A中的情况。关键问题是SSE值应该有多小(通过设置阈值来实现)才能安全地决定是否跳过模式。在快速模式选择中,保持编码质量不变是至关重要的。关键贡献在于直接从视频数据本身找到阈值,避免了任何用户的干预,从而使提出的早期决策算法具有更广泛的实用性。
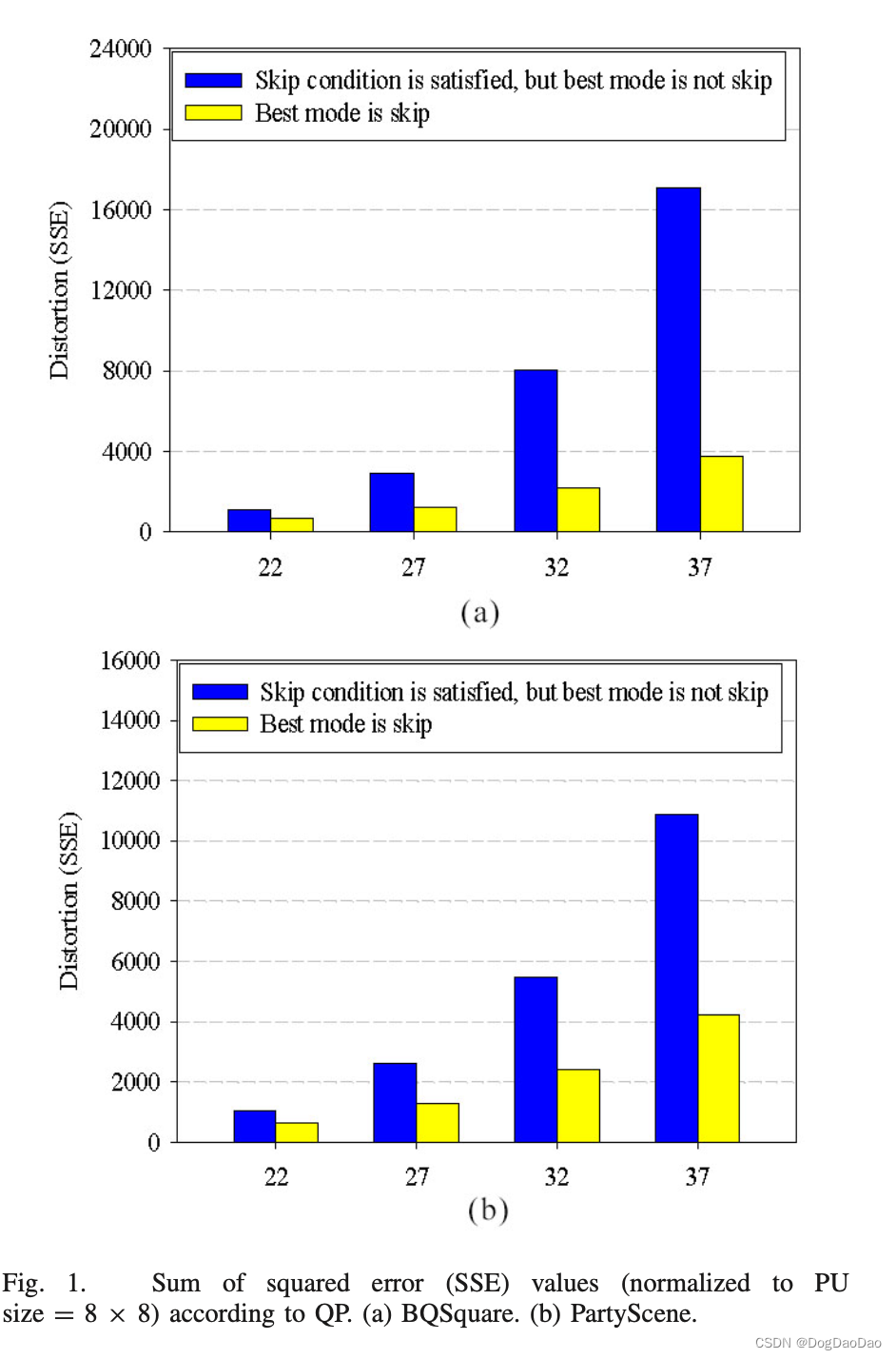
为此,本文首先利用离线训练序列,从运动补偿残差变换系数的均值和方差方面研究了Skip PUs的失真特性。由于Skip PU可以根据CU的大小具有不同的大小,在此分析中,Skip PU的残差被分为8×8块,并对每个块应用8×8离散余弦变换(DCT)。图2显示了Skip块中运动补偿残差的DCT系数的平均值μ(QP)和方差σ 2 (QP),根据每个QP(大小归一化8×8)。
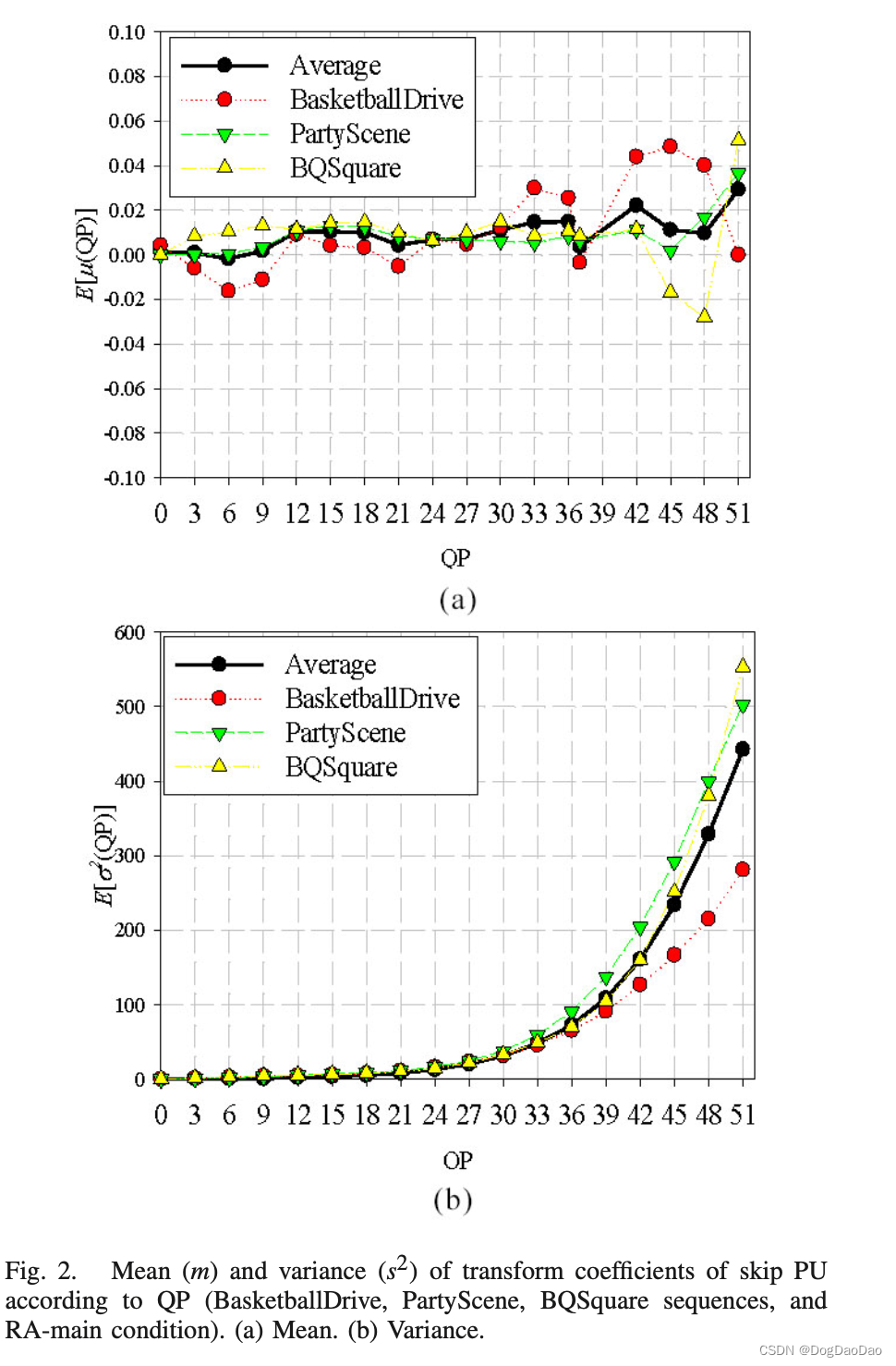
图2(a)中Skip块的平均μ(QP)几乎为零,与QP无关,通过注意以下内容可以很好地理解:

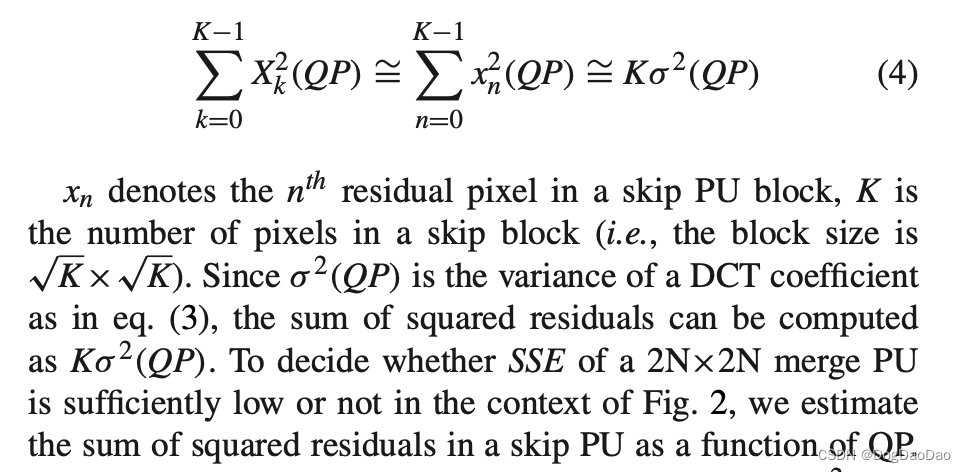
为此,我们通过对图2(b)中带有黑色圆圈的虚线进行曲线拟合(如图2(b)中带有黑色圆圈的“序列上的平均”)来建模σ2(QP)和QP之间的关系,如下所示:
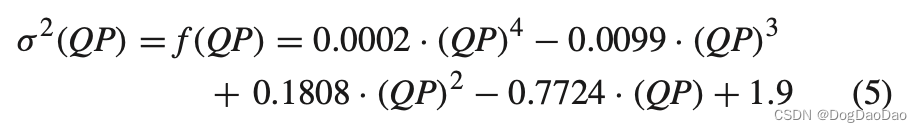
利用公式.(4)和公式.(5),可以估计一个跳跃PU相对于QP的失真(即SSE),如下所示:

提出早期跳过模式决策
如第二节中的skip条件所述,HEVC中的Skip模式被视为Merge模式的一种情况。Merge候选源来自空间或时间上相邻的PUs。为了判断给定的CU是否可以合并,在图3中MERGE_2N×2N的过程中,所提出的方法依次在待测PU需要合并的Merge候选块中搜索一个块。如果成功找到一个,选中的Merge候选项将通过发送其索引通知解码器。
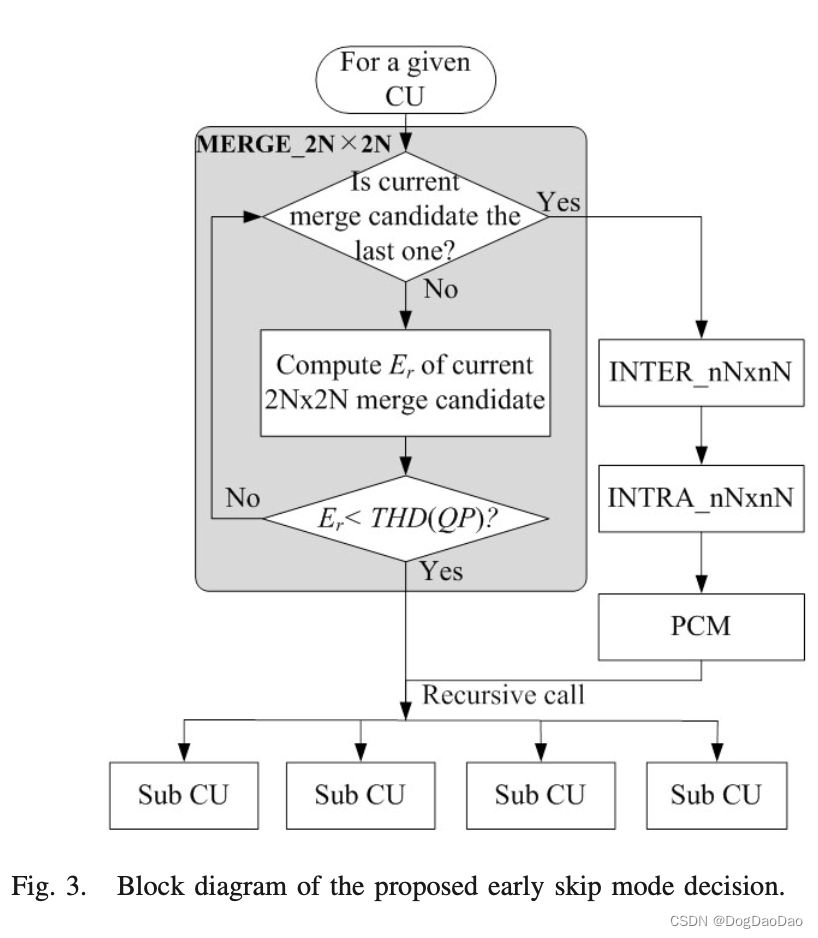
在图3中,INTER_nN×nN的过程表示剩余模式间决策,INTRA_nN×nN表示INTRA_2N×2N和INTRA_N×N模式决策过程。在图3的MERGE_2N×2N过程中,所提方法计算当前2N×2N PU与其Merge候选PU之间的误差平方和Er,并在满足以下条件时提前确定Skip模式:

由式(7)提出的决策可以导致Skip模式的早期决策,即使它的残差实际上没有被量化为零。正如上文在第二节中讨论的情形B所述,当设置为跳过模式时,失真会增加,但与相应的比特率降低(即仅向解码器发送跳过标志和候选索引)相比,这种情况很小。这很好地解释了为什么所提出的方法可以在实现与现有方法相当的复杂度降低的同时最小化编码损失。更多细节将在下一节的实验数据分析中进行解释。
实验结果
表II和表III显示了由式(7)选择skip模式为最佳模式的条件概率。

表IV和V显示了所提方法与HM中其他三种快速编码方法的性能比较。在RA-main和LD-main两种情况下,编码时间分别降低了33.3%和30.6%。其中 AST 计算公式如下公式 9:
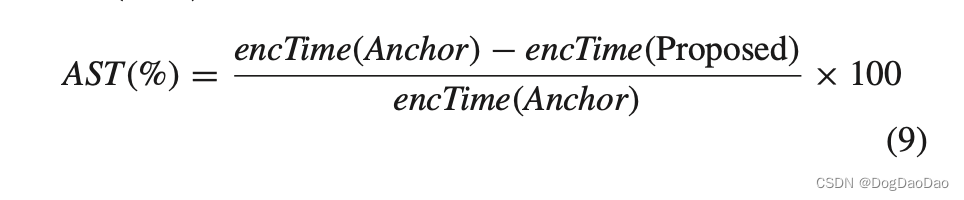
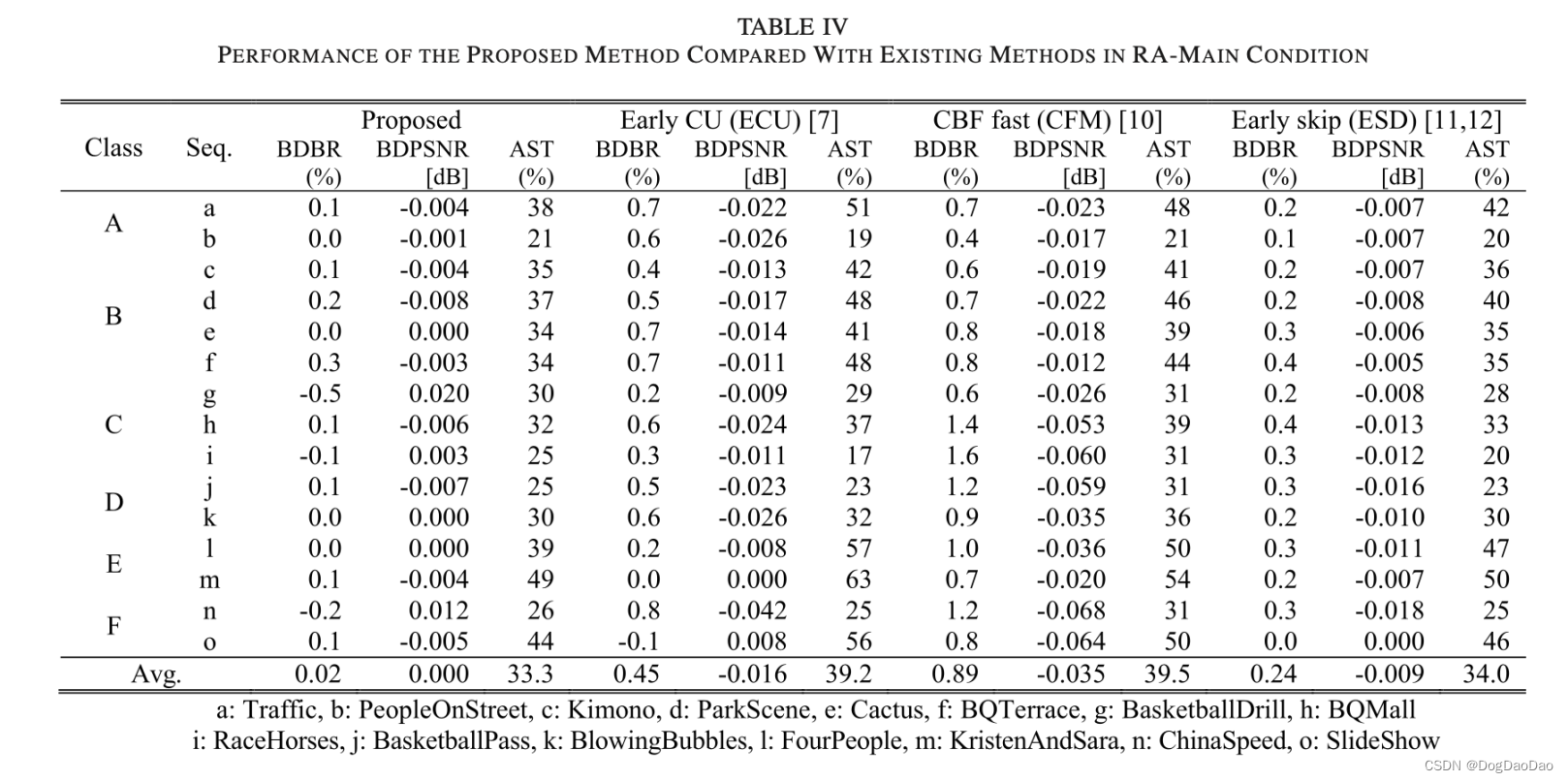
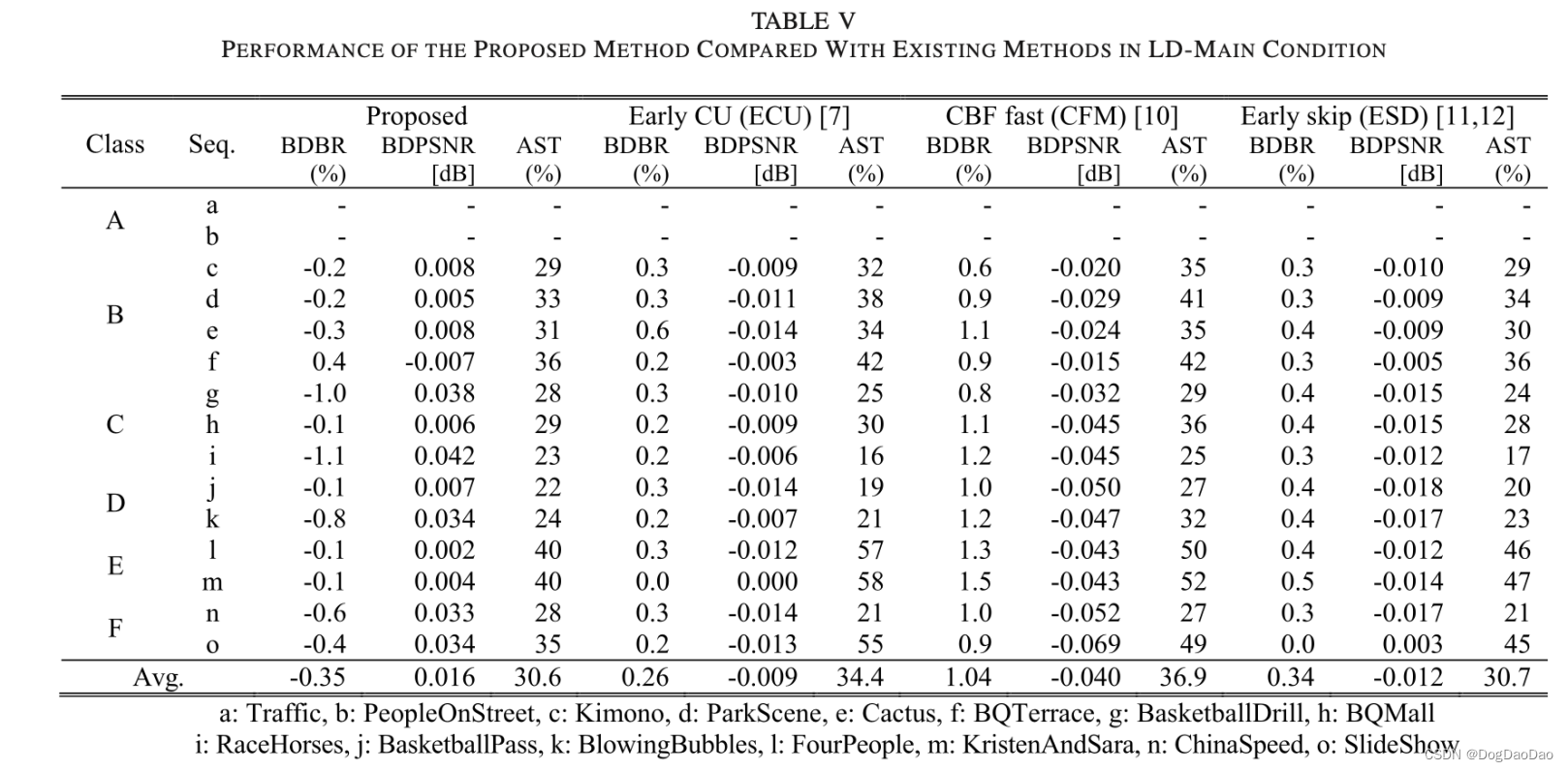
为了更详细地了解所提方法如何在几乎没有编码损失的情况下减少编码时间,图4分析了三种情况下当前CU的平均失真:如图4所示,在情况ii)下,所提方法的失真度要远低于情况i)。这意味着,即使所提方法和其他方法一样,在早期跳过决策时也会出现错误,但由于这种错误判断块的平均失真度非常小,因此预计对编码质量的影响最小。当案例ii)与案例iii)相比时,所提方法更令人鼓舞的效果很容易理解。图4显示案例ii)的失真仅略大于案例iii)。这说明所提方法错误判断为跳过的块与参考方法具有几乎相似(或略大)的失真(注意,它是通过完全RD优化的决策)。
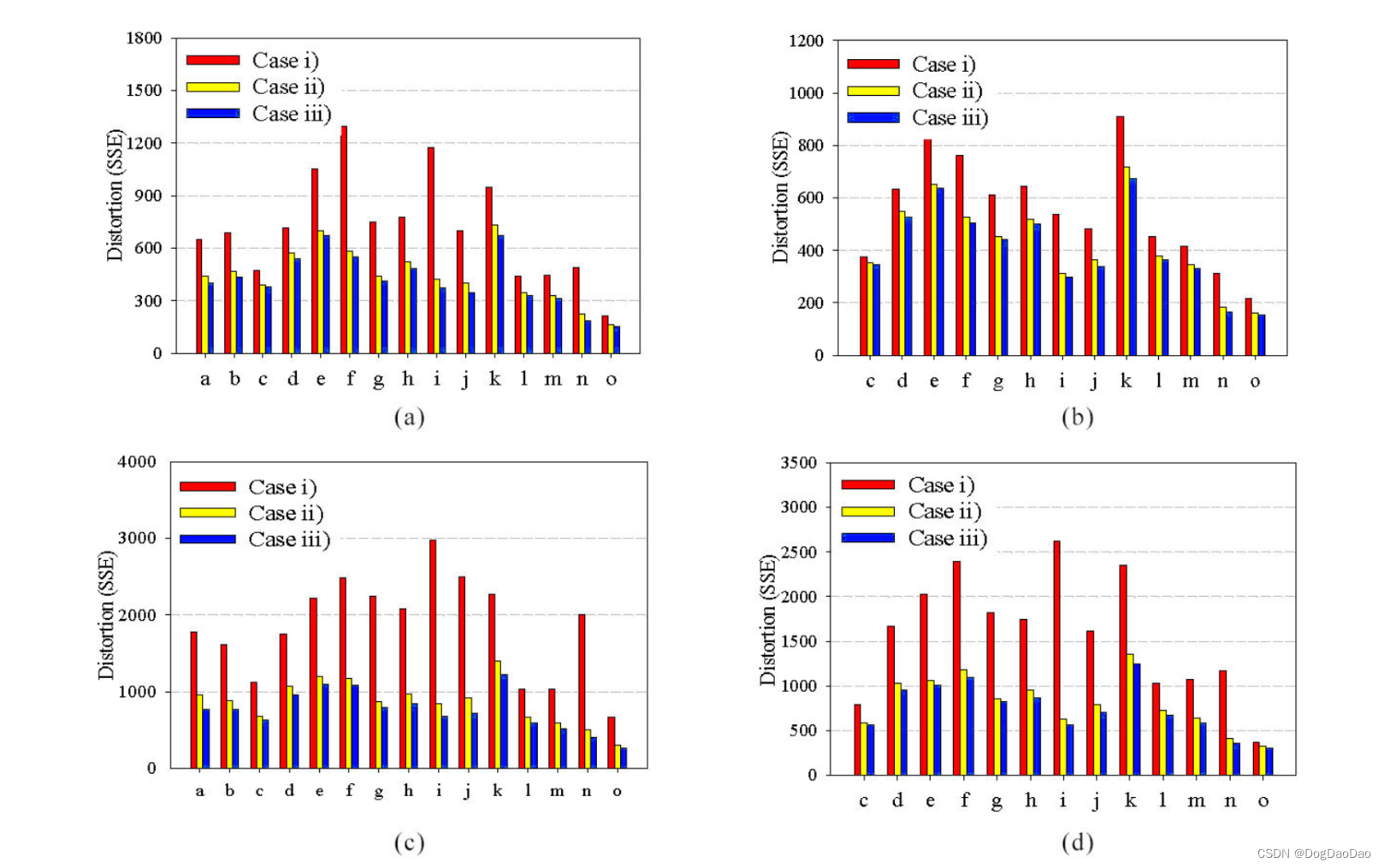
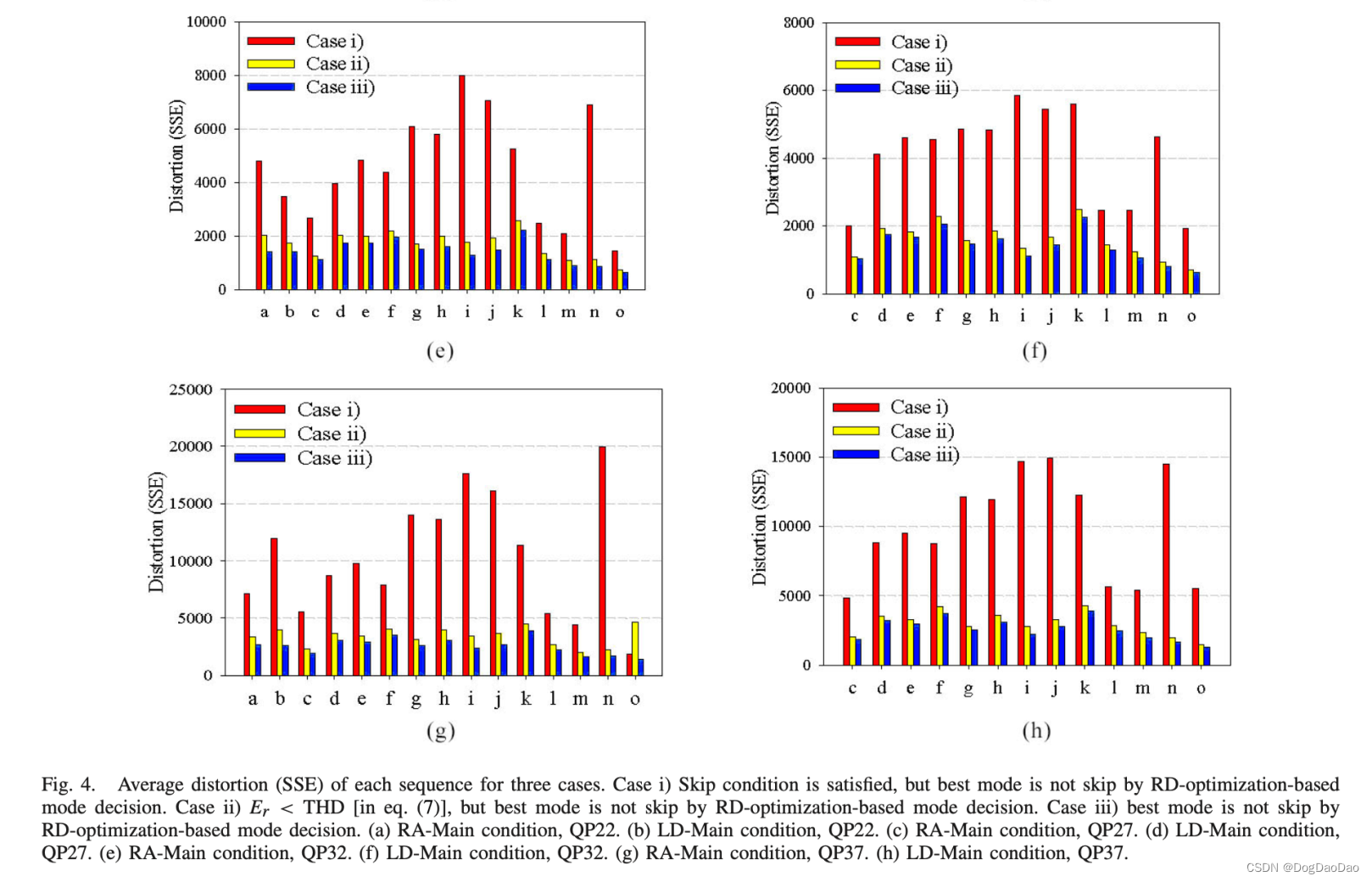
为了更客观地理解这一点,图5比较了典型位置(参见图5中的黑盒),其中skip PU是由参考方法和所提出的方法确定的。如图5所示,所提出的方法比参考方法选择了更多的Skip PUs——这解释了为什么编码时间是可以减少的。正如预期的那样,虽然那些高纹理区域(例如,如图5中的草地区域)在两种方法中都没有任何跳跃PUs(如预期的那样),但所提出的方法发现的额外跳跃PU都位于剩余能量非常低的相对均匀区域。因此,在早期的跳过决策中任何偶然的错误都将导致最小的感知质量损失。

表VI和VII显示了该方法与其他快速方法(即ECU[7]和CFM[10])结合的性能。
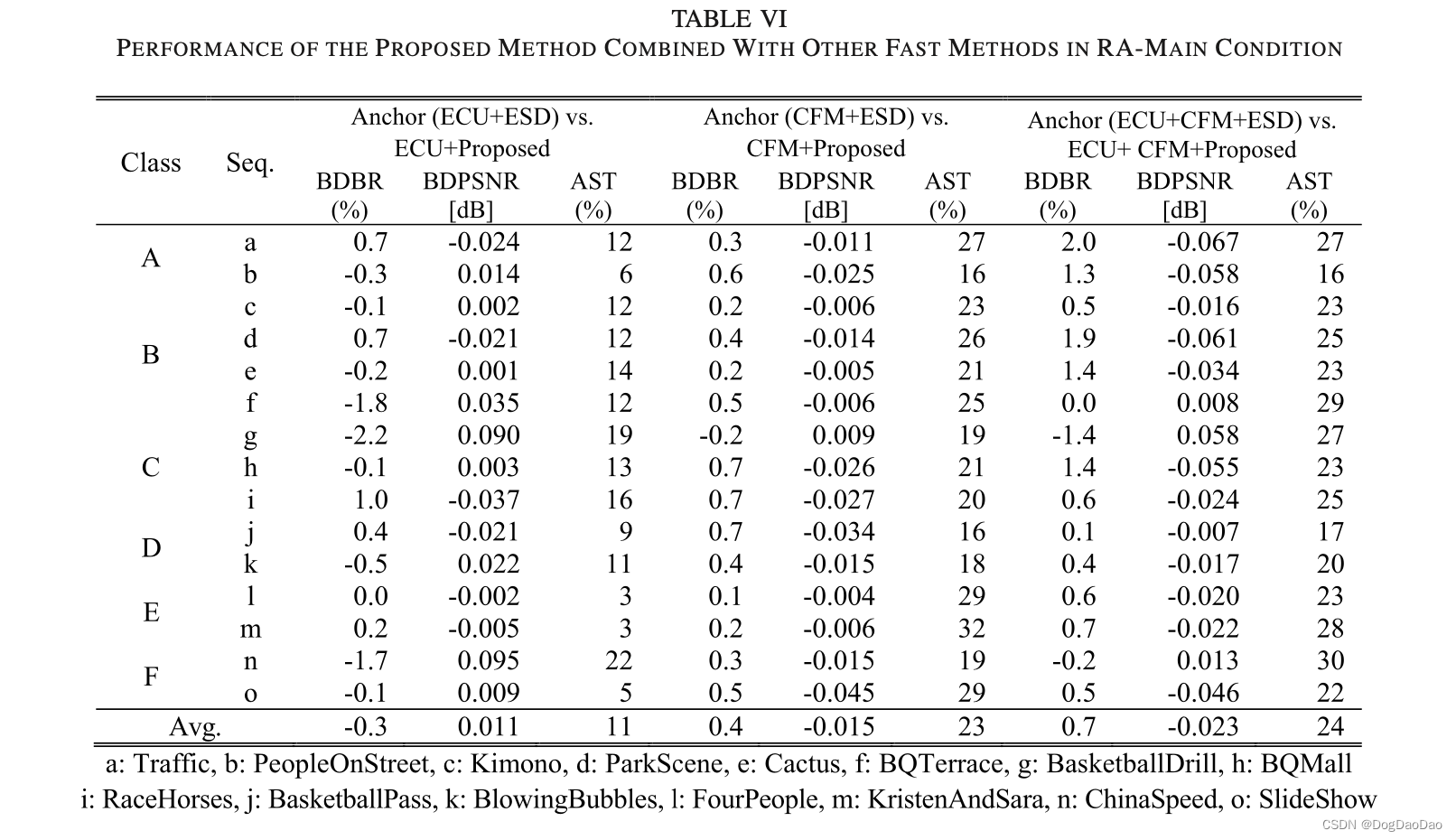
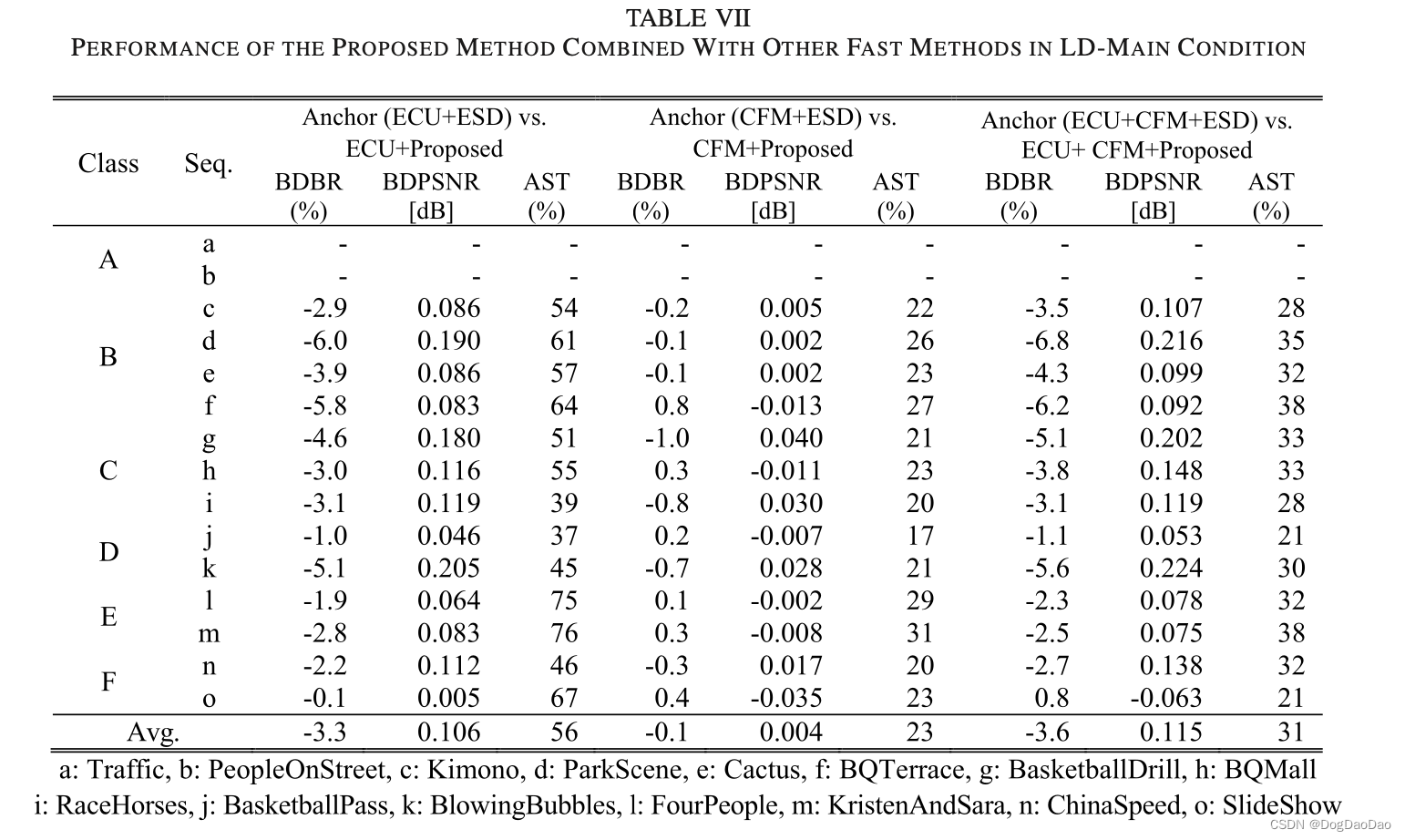
实验结果表明,该方法在不损失任何编码损失的情况下,大大缩短了编码时间,对高质量的编码应用具有重要意义。与ESD方法[11]、[12]在2N×2N AMVP过程中执行运动估计并在满足跳跃条件时选择跳过相比,所提出的方法即使没有额外的处理,也会在其失真足够低时决定跳过PU(注意所提出的方法不执行任何运动估计过程来决定跳过PU)。因此,与ESD方法相比,该方法的编码损失要小得多,同时也节省了大量的时间。由于早期跳过决策所需的阈值是直接从视频数据本身估计的,因此具有更广泛的实际应用前景。
结论
为了在几乎没有编码损失的情况下减少HEVC编码器的处理时间,提出了一种早期skip模式选择方法。该方法可以从编码状态下的视频数据中直接估计出跳跳PU的阈值。根据估计的阈值,当当前2N×2N合并PU失真小于估计阈值时,该方法决定跳过。与HM12.0编码器相比,在几乎没有编码损失的情况下,所提方法使HEVC的编码复杂度在随机接入主条件下降低了30%以上,在低时延条件下降低了26%以上。这种方法对于高质量的编码应用非常有用。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- SQL进阶2
- 【JavaScript】es6开发常用技巧
- 租房别再傻傻的扯网线了!随身WiFi靠谱品牌推荐,哪个随身WiFi最好用
- 免费电子书!18个文学小说下载阅读资源网站,这些宝藏网站请收藏!
- YOLOv5优化:独家创新(SC_C_Detect)检测头结构创新,实现涨点 | 检测头新颖创新系列
- 华为云Stack 8.X流量模型分析(六)
- 代码随想录算法训练营第2天 | 977.有序数组的平方、209.长度最小的子数组、59.螺旋矩阵II
- 【ceph】pg down的处理流程
- 【Three.JS学习笔记(一)】几何体全家福
- 一文搞懂Python Web开发 Django