Unity | Shader基础知识番外（向量数学知识速成）

发布时间：2024年01月03日

一、向量定义

二、计算向量

三、向量的加法（连续行走）

3 叉乘的计算（这里看不懂就百度叉乘计算）

八、欢迎收看Shader专栏

一、向量定义

向量：从一个点到另一个点的箭头。

例：假如现在有两个点，A（0,0）和B点（4,5）。

假如从A走向B（如图1），箭头为：

假如从B走向A（如图2），箭头为：

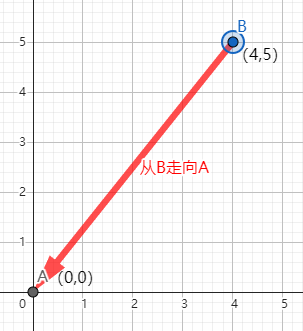
我们会用A（0,0）表示点A，

我们会用B（4,5）表示点B，

问题，我们用什么表示和区分这两个箭头？

答：如果从A走向B，我们就写成 $\vec{AB}$ ，如果从B走向A，就写成 $\vec{BA}$ （是不是很形象）。

字母确定了，可数字怎么办？

答：因为横坐标x是向左为正，纵坐标y是向上为正。

我们从A（0,0）走向B（4,5）等于向右走4格，向上走5格，所以是 $\vec{AB}$ （4，5），

反之，如果从B（4,5）走向A（0,0）等于向左走4格，向下走5格，所以是 $\vec{BA}$ （-4，-5），

所以在表达向量时，写的是箭头起点到箭头终点是如何走过去。

二、计算向量

（如图3）如果我们随意画出两个点A（1,3），B（4,5）

通过数格子，我们可以得出 $\vec{AB}$ （3，2），但这个数字，我们也可以算出来，通过终点的B（4,5）中的x减去A（1,3）的x：4-1=3，通过终点的B（4,5）中的y减去A（1,3）的y：5-3=2

也可以得出： $\vec{AB}$ （3，2）

所以：终点的坐标，减去起点的坐标，就是向量的数值

三、向量的加法（连续行走）

（如图4）我们画两个连着的向量 $\vec{AB}$ （1，3）和 $\vec{BC}$ （3，2）：

从图中（如图5）我们可以看出，我们从A走到B，又从B走到C，这种连着走的向量我们可以相加，实际上两个向量就是从A走到了C，横着向右走了4格，向上走了5格。

$\vec{AB}$ （1，3）+ $\vec{BC}$ （3，2）= $\vec{AC}$ （1+3，3+2）= $\vec{AC}$ （4，5）

四、向量的长度

（如图6）假如我希望计算 $\vec{AC}$ （4，5）的长度，通过我们学过的勾股定理就得出

AC =? $\sqrt{4^{2}+5^{2}}$

所以：向量的长度为 $\sqrt{x^{2}+y^{2}}$

五、单位向量

单位向量：向量长度是1

把任何一个向量变成单位向量，只需要除以向量的长度。

例：向量（3,4），长度是5，希望长度变为1，就直接集体除以5。

所以，向量（3,4）的单位向量就是（3/5,4/5）。

六、向量的点积

1 计算

设向量a(1,2)和向量b（3,4）点乘

算法1：

$\vec{a}\cdot \vec{b}=(x_{1}\times x_{2})+(y_{1}\times y_{2})=(1\times 3)+(2\times 4)=3+8=11$

算法2：

$\vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|cos\theta=\sqrt{1^{2}+2^{2}}\sqrt{3^{2}+4^{2}}cos\theta$

算法2算到这一步就停了，因为不知道cosθ，

可是算法1和算法2的结果是相同的。

$\sqrt{1^{2}+2^{2}}\sqrt{3^{2}+4^{2}}cos\theta=11$

所以，可以算出 $cos\theta=\frac{11}{\sqrt{1^{2}+2^{2}}\sqrt{3^{2}+4^{2}}}=0.98$

最后θ≈11.5°

2 作用

为啥要算点积？（我们把上面的向量a和向量b画出来）（如图7）

我原本面向A（向量a）,现在我想面向B，我应该旋转多少度？

答：刚才算过了：11.5°

备注（以下结论的推导过程自己百度）：

$\vec{a}\cdot \vec{b}$ >0? ? ? ? a和b的夹角0-90度之间

$\vec{a}\cdot \vec{b}$ =0? ? ? ? a和b的夹角为90度

$\vec{a}\cdot \vec{b}$ <0? ? ? ? a和b的夹角大于90度

七、向量的叉乘

1 承上启下

第六部分我们知道了旋转角度，不知道聪明的你有没有发现，其实，你只知道了角度，不知道是顺时针旋转还是逆时针旋转。叉乘就事帮助我们判断是哪个方向的旋转的。

2 叉乘结论

当叉乘结果<0? ? ? ? 顺时针旋转

当叉乘结果>0? ? ? ? 逆时针旋转

叉乘结果=0? ? ? ? ? ? 不用旋转

3 叉乘的计算（这里看不懂就百度叉乘计算）

我们还是计算向量a(1,2)和向量b（3,4）叉乘，因为叉乘需要x,y,z才能计算，此时相当于我们的z是0，所以我们的向量为a(1,2,0)和向量b（3,4,0）。

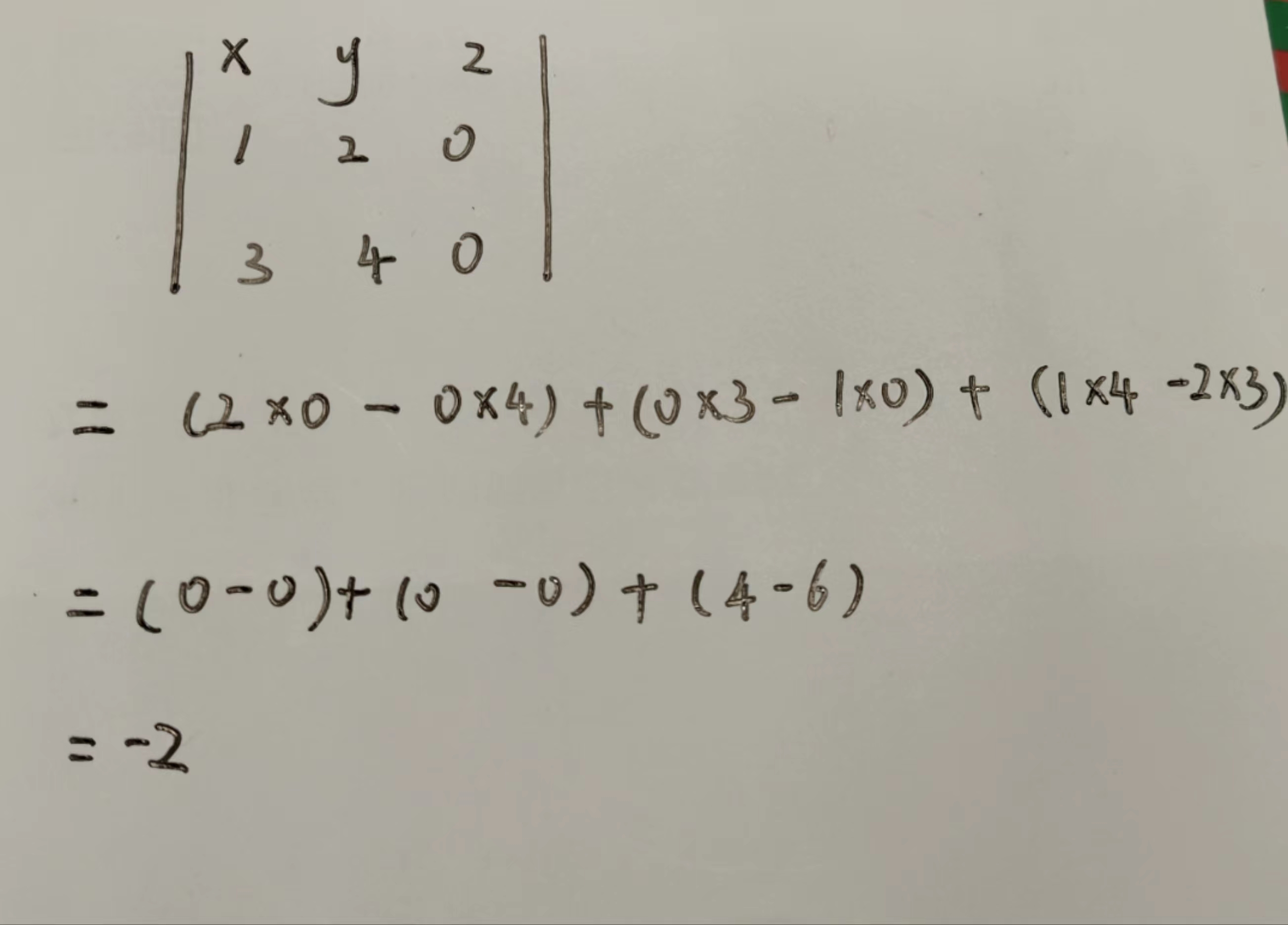
此时是-2<0所以，我们只需要逆时针旋转11.5°，就可以从向量a的方向变成向量b的方向。

八、欢迎收看Shader专栏

https://blog.csdn.net/weixin_49427945/category_12525804.html

文章来源:https://blog.csdn.net/weixin_49427945/article/details/135344810
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！