day21 二叉树part07

530. 二叉搜索树的最小绝对差

简单
给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数，其数值等于两值之差的绝对值。

// 自己写的解法
class Solution {
    Integer pre;
    int res = Integer.MAX_VALUE;
    public int getMinimumDifference(TreeNode root) {
        inOrder(root);
        return res;
    }
    public void inOrder(TreeNode node) {
        if (node == null) return;
        inOrder(node.left);
        if (pre != null) { // 当遍历到的节点不是中序遍历数组的第一个节点
            res = res < node.val - pre ? res : node.val - pre;
        }
        pre = node.val;
        inOrder(node.right);
    }
}

// 卡尔的方法，和我的区别不大
class Solution {
    TreeNode pre;// 记录上一个遍历的结点
    int result = Integer.MAX_VALUE;
    public int getMinimumDifference(TreeNode root) {
       if(root==null)return 0;
       traversal(root);
       return result;
    }
    public void traversal(TreeNode root){
        if(root==null)return;
        //左
        traversal(root.left);
        //中
        if(pre!=null){
            result = Math.min(result,root.val-pre.val);
        }
        pre = root;
        //右
        traversal(root.right);
    }
}

501. 二叉搜索树中的众数

简单
给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。
如果树中有不止一个众数，可以按 任意顺序 返回。
假定 BST 满足如下定义：
结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树

注意啊，这里二叉搜索树的定义是小于等于和大于等于，其实这个题把它当做提取升序数组的众数就行，相等的数在升序数组里一定是挨着的，真正的难点在于它可能不止一个众数

// 自己写的解法
class Solution {
    Stack<Integer> stk = new Stack<>();
    int max_fre = -1; // 记录最大的那个频率
    int cur_fre = 0; // 记录当前节点的频率
    TreeNode pre = null; // 记录前一个节点

    public int[] findMode(TreeNode root) {
        inOrder(root);
        int stkSize = stk.size();
        int[] res = new int[stkSize];
        for (int i = 0; i < stkSize; i++) {
            res[i] = stk.pop();
        }
        return res;
    }

    public void inOrder(TreeNode node) {
        if (node == null)
            return;
        inOrder(node.left);
        if (pre != null) { // 当不是中序遍历数组的第一个节点时
            if (pre.val != node.val) { // 当出现了一个新的val值时
                cur_fre = 1;
            } else { // 当val等于前一个val值时
                cur_fre++;
            }
        } else { // 当此节点为第一个节点时
            cur_fre = 1;
        }

        if (cur_fre > max_fre) { // 当前val的值频率大于最大频率，
            while (!stk.isEmpty()) { // 清空栈
                stk.pop();
            }
            max_fre = cur_fre;
            stk.push(node.val); // 压入新的最大频率对应的数
        } else if (cur_fre == max_fre) { // 如果和最大频率一样大也要入栈
            stk.push(node.val);
        }
        pre = node;
        inOrder(node.right);
    }
}

// 卡尔用的是 ArrayList<Integer> resList = new ArrayList<>();
class Solution {
    ArrayList<Integer> resList;
    int maxCount;
    int count;
    TreeNode pre;

    public int[] findMode(TreeNode root) {
        resList = new ArrayList<>();
        maxCount = 0;
        count = 0;
        pre = null;
        findMode1(root);
        int[] res = new int[resList.size()];
        for (int i = 0; i < resList.size(); i++) {
            res[i] = resList.get(i);
        }
        return res;
    }

    public void findMode1(TreeNode root) {
        if (root == null) {
            return;
        }
        findMode1(root.left);

        int rootValue = root.val;
        // 计数
        if (pre == null || rootValue != pre.val) {
            count = 1;
        } else {
            count++;
        }
        // 更新结果以及maxCount
        if (count > maxCount) {
            resList.clear();
            resList.add(rootValue);
            maxCount = count;
        } else if (count == maxCount) {
            resList.add(rootValue);
        }
        pre = root;

        findMode1(root.right);
    }
}

236. 二叉树的最近公共祖先

中等
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

难点：注意，p, q 一定是存在于给定的二叉树中，如果没有这个条件，返回的节点是错的，经过我验证过的，因为一定存在于给定的二叉树中，所以以下条件才能站住脚：

难点：自底向上要用后序遍历，而且因为这俩节点一定在树中，那么，就一定存在一个他们的公共祖先!

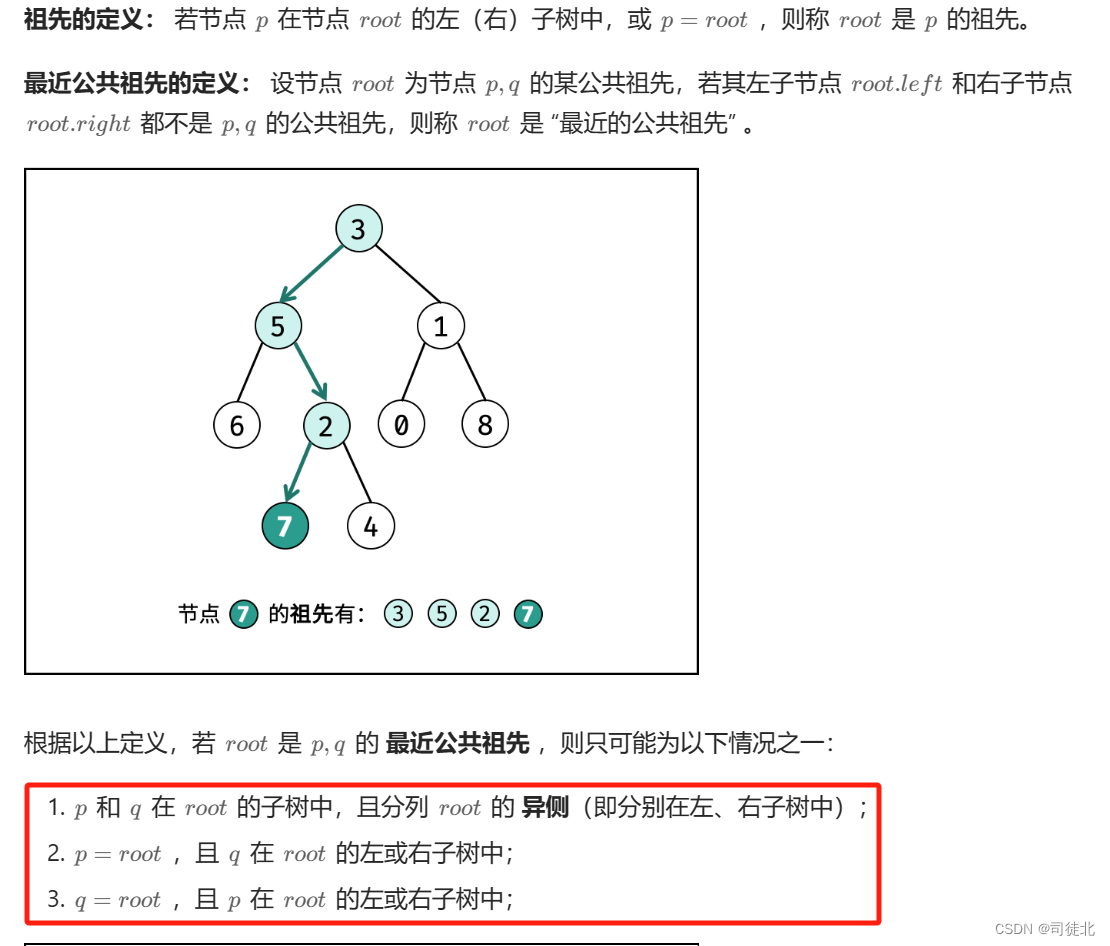
这题很难，我到现在都没有特别想明白

// 大佬的代码
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q) {
            //只要当前根节点是p和q中的任意一个，就返回（因为不能比这个更深了，再深p和q中的一个就没了）
            return root;
        }
        //根节点不是p和q中的任意一个，那么就继续分别往左子树和右子树找p和q
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        //p和q都没找到，那就没有
        if(left == null && right == null) {
            return null;
        }
        //左子树没有p也没有q，就返回右子树的结果
        if (left == null) {
            return right;
        }
        //右子树没有p也没有q就返回左子树的结果
        if (right == null) {
            return left;
        }
        //左右子树都找到p和q了，那就说明p和q分别在左右两个子树上，所以此时的最近公共祖先就是root
        return root;
    }
}

// 我抄的大佬的